KL 散度（Kullback–Leibler divergence），用于衡量两个概率分布之间的差异^[1]，也叫做相对熵（Relative entropy）。

从信息量说起

任何事件都会承载着一定的信息量，包括已经发生的事件和未发生的事件，只是它们承载的信息量会有所不同。

例如，如昨天下雨这个已知事件，因为已经发生，既定事实，那么它的信息量就为 0。如明天会下雨这个事件，因为未有发生，那么这个事件的信息量就大。

由此可知，事件发生的概率越小，其信息量越大。

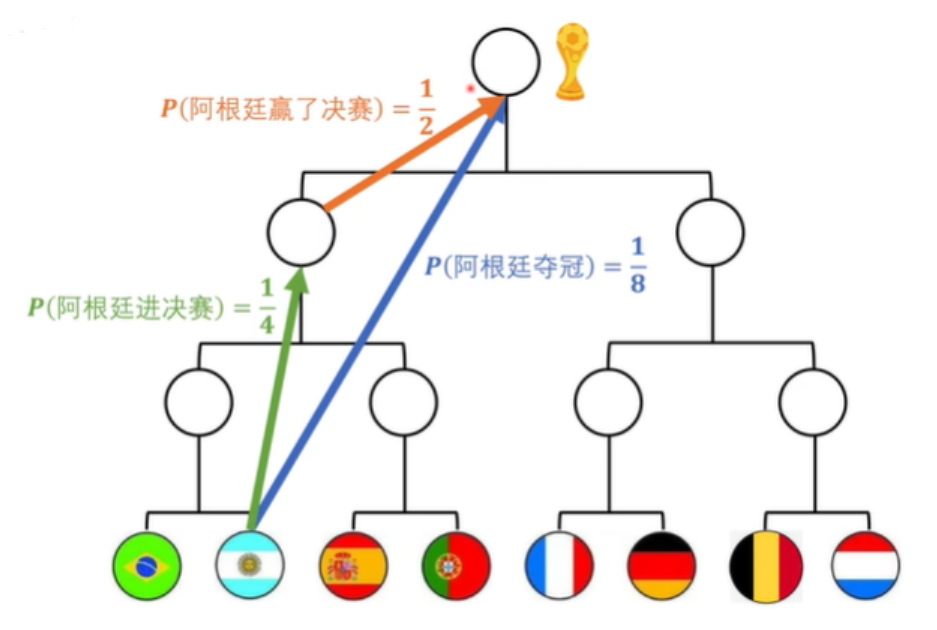
再如，阿根廷夺冠的信息量是等于阿根廷进决赛和进决赛之后阿根廷赢了比赛信息量是相等的，同时这也是概率事件，所以得出：

为满足 ，则自然可以使用 来定义信息量，即

由于事件发生的概率越小，其信息量越大，因此需要添加一个 '-' 号，而底数则可以有不同的选择。当底数是以 2 为底数时，信息量的单位是比特。

因此，其定义为：

其中， 表示一个离散型随机变量，概率分布函数为 ， 表示事件 发生的概率。

熵是信息量的期望

那么如果我们把这个事件的所有可能性罗列出来，就可以求得该事件信息量的期望，

信息量的期望就是熵，其定义为：

如果熵比较大（即平均编码长度较长），意味着这一信息有较多的可能状态，相应的每个状态的可能性比较低；因此每当来了一个新的信息，我们很难对其作出准确预测，即有着比较大的混乱程度/不确定性/不可预测性^[3]。

度量两个分布的差异

KL 散度旨在衡量近似分布 与真实分布 之间匹配程度，其形式上定义为：

直观地说，这衡量的是给定任意分布偏离真实分布的程度。如果两个分布完全匹配，那么有

对于连续的分布，只不过就是将求和变成积分，概率改成概率密度，定义式如下：

接下来我们从熵的角度来理解一下 KL 散度，将离散分布的 KL 散度的定义式展开：

证明：

以离散分布为例，由琴生不等式得：

交叉熵与 KL 散度

根据上面的 KL 公式可以看到，KL散度 = 交叉熵 - 目标分布熵
。

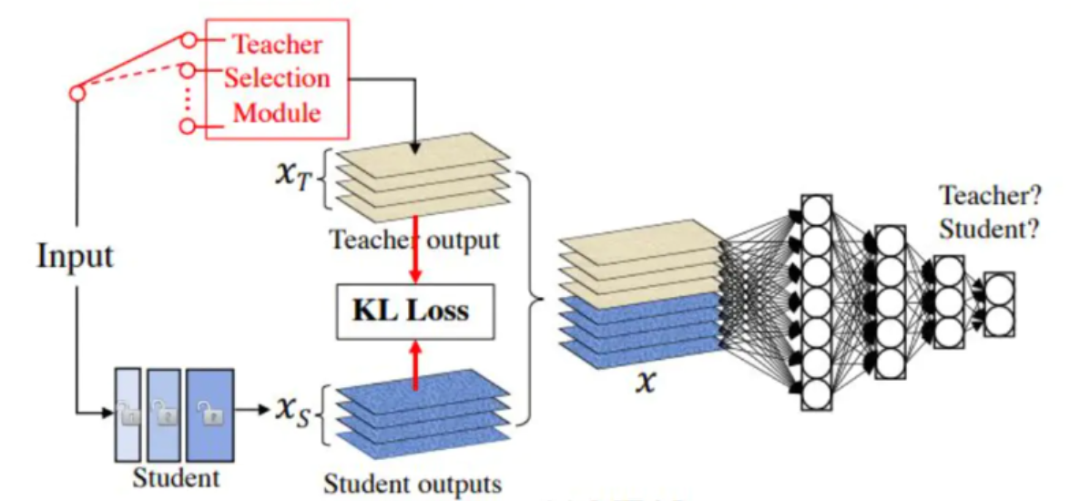
知道了模型分布与目标分布差异可用交叉熵代替 KL 散度的条件是目标分布为常数。如果目标分布是有变化的（如同为猫的样本，不同的样本，其值也会有差异），那么就不能使用交叉熵，例如蒸馏模型的损失函数
就是 KL 散度，因为蒸馏模型的目标分布也是一个模型，该模型针对同类别的不同样本，会给出不同的预测值（如两张猫的图片 a 和 b，目标模型对 a 预测为猫的值是 0.6，对 b 预测为猫的值是 0.8）。

交叉熵用来衡量在给定的真实分布下，使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小^[5]。这也是为什么在机器学习中的分类算法中，我们总是最小化交叉熵，因为交叉熵越低，就证明由算法所产生的策略最接近最优策略，也间接证明我们算法所算出的非真实分布越接近真实分布。

参考资料