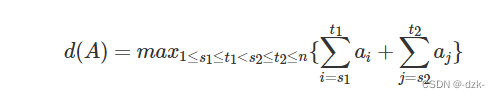文章目录

• 写在前面
• 一、题目
• 1、原题链接
• 2、题目描述
• 二、解题报告
• 1、思路分析
• 2、时间复杂度
• 3、代码详解
• 三、知识风暴
• 线性DP

写在前面

本人CSDN博客主页：这里

一、题目

1、原题链接

1051. 最大的和

2、题目描述

对于给定的整数序列 A={a1,a2,…,an}，找出两个不重合连续子段，使得两子段中所有数字的和最大。

我们如下定义函数 d(A)：

我们的目标就是求出 d(A)。

输入格式

第一行是一个整数 T，代表一共有多少组数据。

接下来是 T 组数据。

每组数据的第一行是一个整数，代表数据个数据 n，第二行是 n 个整数 a1,a2,…,an。

输出格式

每组数据输出一个整数，占一行，就是 d(A) 的值。

数据范围

1≤T≤30,2≤n≤50000,|ai|≤10000

输入样例：

1
10
1 -1 2 2 3 -3 4 -4 5 -5

输出样例：

13

样例解释
在样例中，我们取{2,2,3,-3,4}和{5}两个子段，即可>得到答案。

二、解题报告

1、思路分析

思路来源：y总讲解视频
y总yyds

（1）利用求单段连续子段和的方法，将所有子段和处理出来。
（2）单段连续子段和最大求解方法：

• dp[i]表示以a[i]结尾的所有连续子段和的最大值。
• 可以将dp[i]分为两部分：①只包含a[i]②不仅包含a[i]还包含a[i]之前的某些数。
• 可知这两部分和分别为a[i]和dp[i-1]+a[i]。
• 所以转移方程为 dp[i]=max(a[i],dp[i-1]+a[i])即dp[i]=max(0,dp[i-1])+a[i]。

（3）对数组序列进行 前后缀分解，利用g[i]记录所有从1 ~ i中的最大子段和，h[i]记录所有从i ~ n中的最大子段和。
（4）枚举i的所有取值，两个连续子段的最大和即为g[i]+h[i+1]的最大值。

2、时间复杂度

时间复杂度为O(n)

3、代码详解

#include <iostream>
#include <algorithm>
using namespace std;
const int N=50010,INF=1e9;
int a[N],h[N],g[N],dp[N];
int T,n;
int main(){
    cin>>T;
    while(T--){
        cin>>n;
        for(int i=1;i<=n;i++) cin>>a[i];
        dp[0]=g[0]=-INF;     //非法状态设置为负无穷
        //正着求一遍单段连续子段和
        for(int i=1;i<=n;i++){
            dp[i]=max(dp[i-1],0)+a[i]; //单段连续子段和的转移方程 
            g[i]=max(g[i-1],dp[i]);   //g[i]存储前1~i中子段和的最大值，如果1~i中的子段和最大值dp[i]比1~i-1中连续子段和最大值g[i-1]大，则g[i]=dp[i]，否则g[i]=g[i-1]
        }
        dp[n+1]=h[n+1]=-INF; //非法状态设置为负无穷
        //倒着求一遍单段子连续段和
        for(int i=n;i>=1;i--){
            dp[i]=max(dp[i+1],0)+a[i];    //单段连续子段和的转移方程
            h[i]=max(h[i+1],dp[i]);   //h[i]存储i+1~n中连续子段和的最大值，类似g[]  
        }
        int ans=-INF;    //两段子段和的最大值可能是负数，所以将ans初始化为负无穷
        //遍历i的取值，找到两段连续子段和的最大值
        for(int i=1;i<=n;i++) ans=max(ans,g[i]+h[i+1]);
        cout<<ans<<endl;
    }
    return 0;
}

三、知识风暴

线性DP