

Join Reorder是数据库优化领域中最为经典备受关注的问题。Join Reorder的问题可以描述为给定一条多表Join的SQL,输出一个最优的Join顺序,使得查询性能最优。在不同的数据库实现中Join Reorder的具体算法各有不同,本文总结了各种流行数据库中Join Reorder的实现方式及其优劣势,最后引出云原生数据库PolarDB分布式版基于规则变换的Join Reorder实现算法及其背后的思考。

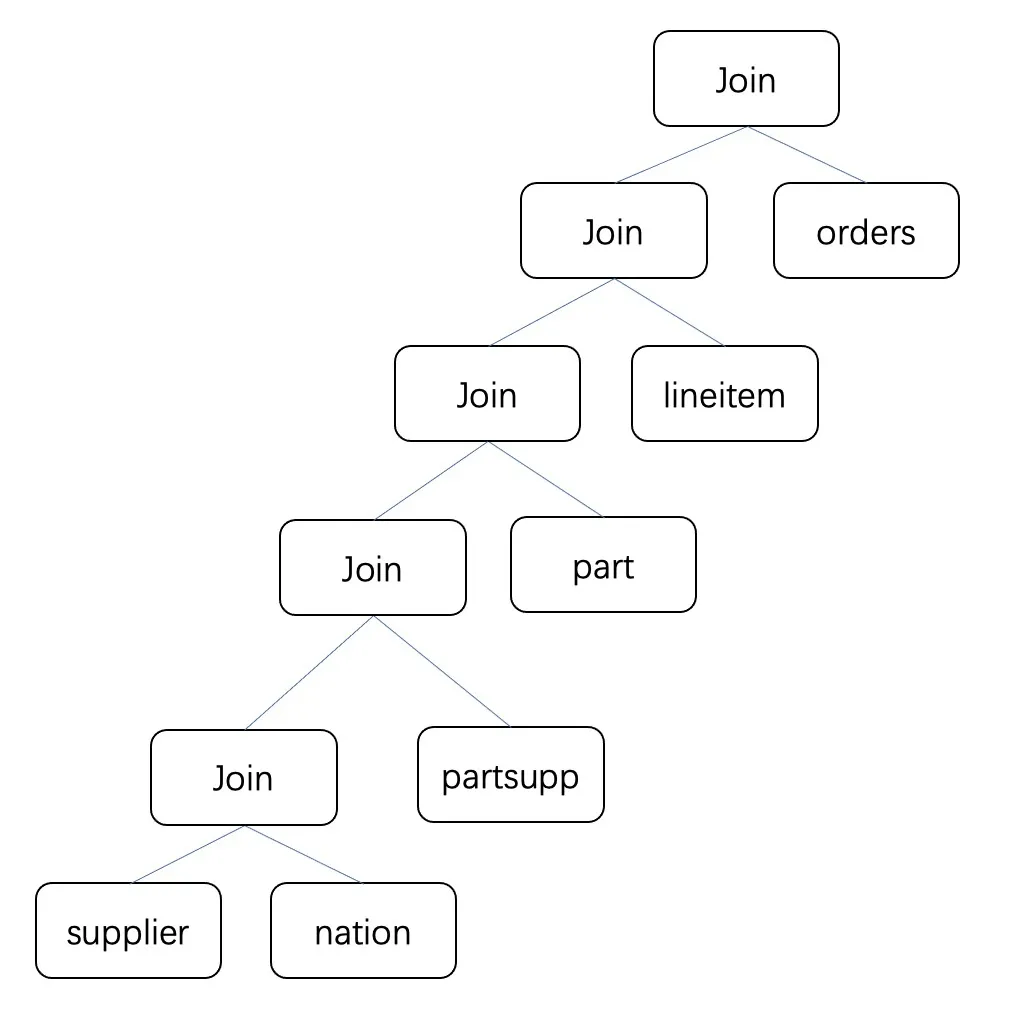
SELECT nation,o_year,sum(amount) AS sum_profitFROM(SELECT n_name AS nation,extract(YEARFROM o_orderdate) AS o_year,l_extendedprice * (1 - l_discount) - ps_supplycost * l_quantity AS amountFROM part,supplier,lineitem,partsupp,orders,nationWHERE s_suppkey = l_suppkeyAND ps_suppkey = l_suppkeyAND ps_partkey = l_partkeyAND p_partkey = l_partkeyAND o_orderkey = l_orderkeyAND s_nationkey = n_nationkeyAND p_name LIKE '%green%') AS profitGROUP BY nation,o_yearORDER BY nation,o_year DESC;
Query Graph

Join Tree
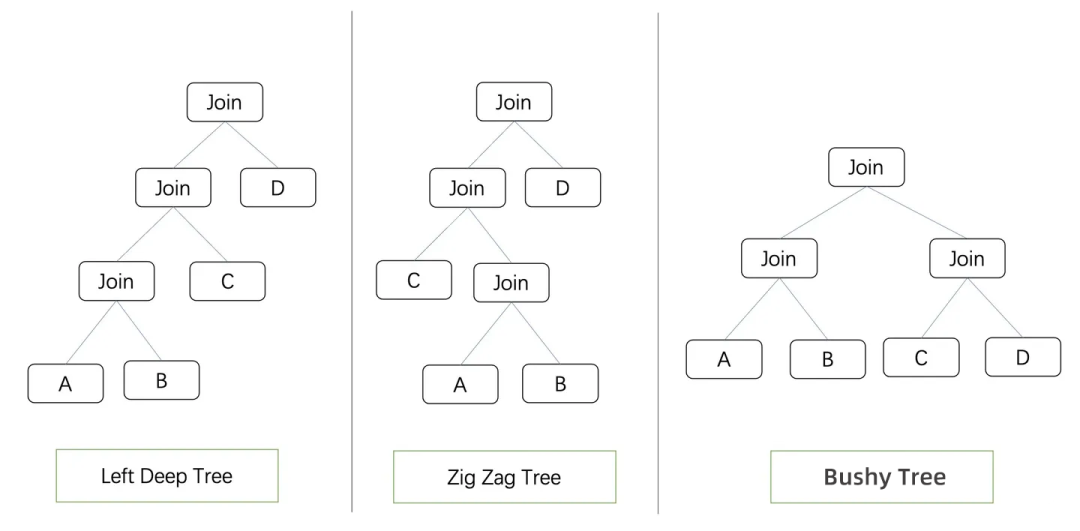
基本上数据库实现一个Join算法的时候只会实现两个输入的情况。Join Tree是一棵二叉树,其中树上的叶子节点代表需要被连接的表,非叶子节点代表Join算子。根据Join Tree的形状,我们可以将其归类为Left Deep Tree, ZigZag Tree, Bushy Tree。Left Deep Tree,就是大名鼎鼎的左深树,Join节点的右侧只能是一个叶子节点,很多数据库都会默认将左深树作为Join Reorder的搜索空间。ZigZag Tree,可以理解为左深树的基础上可以进行左右节点的交换。Bushy Tree,结构最为自由,表可以按照任意顺序Join。
Join Cardinality
LeftRowCount * RightRowCount MAX(LeftCardinality, RightCardinality)
其Le中ftRowCount,RightRowCount分别代表Join左和右输入的行数,LeftCardinality代表左输入Join列的NDV(Number Of Distinct Value)值,RightCardinality同理。特别的,没有Join条件的Cross Join结果行数为LeftRowCount * RightRowCount。
Join Cost
Hash Join的执行代价
CPU代价 = Probe权重 * Probe端数据量 + Build权重 * Build端数据量
Nested Loop Join的执行代价
CPU代价 = Join权重 * 左端数据量 * 右端数据量
CPU代价 = 左端输入数据排序代价 + 右端输入排序代价 + Merge代价

1. 贪心启发式算法,因为速度很快,此类算法适合Join数目较多的情况。
单序列贪心启发式Join Reorder算法
从一张表逐渐到N张表,贪心地选出使得当前Join输出RowCount最小的表加入。按照选出的表序列构建出左深树。[1]
算法流程:搜索空间为左深树,假定输入为N张表,从一张表逐渐到N张表构建出完整的JoinOrder
多序列贪心启发式Join Reorder算法
算法流程:假定输入为N张表的inner join
1. 设置权重Weight[i][j],其中i为第i张表,j为第j张表。权重越大,这两张表应该越先Join。
Weight[i][j] = 3,如果i,j存在等值join条件
Weight[i][j] = 2,如果i,j存在非等值join条件(>, >=, <, <=, !=)
Weight[i][j] = 1, 其它情况(i和j可能是笛卡尔集)
2. 假定序列第一张表为X,第二张表Y选取规则如下
3. 优先考虑Weight[X][Y]大的Y
4. 如果Weight值相等,则考虑Y Join X中Y的Join条件所对应列的Cardinality值,Cardinality越大越优先考虑。(PS:Cardinality越大Join的结果集越小)
5. 第K张表的选择如此类推
6. 最终N张表按照上述选择顺序构造出左深树
GOO算法
● 针对上面贪心启发式只能构造左深树的场景,GOO可以构造出BushyTree
算法流程:假定输入N张表 令T = N张表的集合:
1. while |T| > 1
a. 找到T中两个JoinTree, T[i]和T[j]使得它们的Join结果集最小
b. T = (T \ T[i] \ T[j]) c. T = T U {T[i] join T[j]}
遗传算法(GEQO)
● 每张表可以看作一个基因
● N个不同基因组成一条染色体
1. 随机生成PoolSize个有效的染色体(例如可以限定某些条件)
2. 给染色体池子按照染色体的优秀程度排序
3. 开始迭代第1,2,..k,...generation轮
4. 先从染色体池子按照特定分布取出两条染色作为父和母染色体(这个分布的概率会偏向选择优秀的染色体)
5. 父和母染色体采取一定的重组策略生成孩子染色体。(重组策略有很多种,最简单的是随机取父染色体的一段连续基因片段,之后按照母染色体顺序添加缺失的基因)
6. 将孩子染色体放入染色体池中,并淘汰最差的染色体
7. 染色体的优秀程度通过将染色体构造成Join树后通过CBO评估出代价,代价越低越优秀
深度优先枚举Join Reorder算法
算法流程
1. 表 <= 7时,完全遍历,搜索空间为Left Deep Tree,深度优先遍Join每个顺序(N!复杂度)。考虑每一个序列的代价。
2. 表 >7时,通过遍历的深度控制搜索空间。
3. Join Reorder同时考虑AccessPath索引选择。
4. 索引选择先通过规则匹配出完全匹配主键、唯一键的等值条件。最后再通过cost比较其它未完全匹配的索引及全表扫描。
Bottom-Up枚举的Join Reorder算法
1. S1是Query Graph上的连通子图;
2. S2是Query Graph上的连通子图;
3. S1和S2无交集;
4. S1和S2之间存在边。
算法流程
1. 初始化单表R的BestPlan(R) = R;
2. (自底向上)遍历每个CCP(S1,S2),S = S1 U S2 (有不同的遍历策略[3]可以有DPsize,DPsub等,最好的策略是无Duplicate的DPccp);
3. 计算出S1,S2的BestPlan p1 = BestPlan(S1),p2 = BestPlan(S2),当S1是一张表时,选择该表的最优的AccessPath;
4. CurrPlan = CreateJoinTree(p1,p2),根据已有的Join算法,生成不同的Join来连接p1,p2两个子执行计划;
5. BestPlan(S) = minCost(CurrPlan,BestPlan(S) );
基于规则变换Top-Down枚举的Join Reorder算法
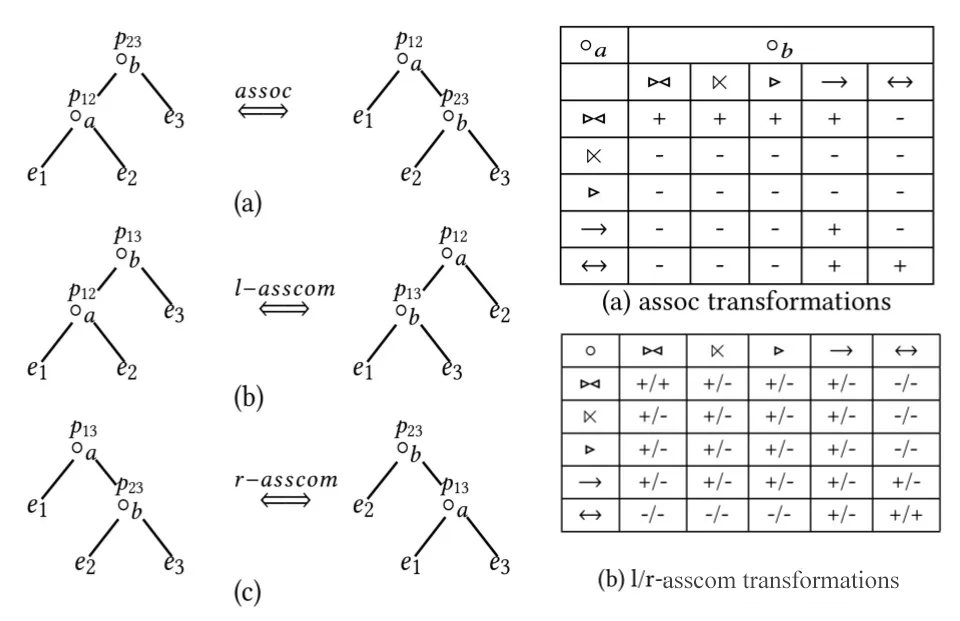
Left Deep Tree: bottom comm规则 : A⨝B → B⨝A, 只应用于左深树的最底下两表 l-asscom规则: (A⨝B)⨝C → (A⨝C)⨝B
Zig-Zag Tree: comm规则 : A⨝B → B⨝A l-asscom规则 : (A⨝B)⨝C → (A⨝C)⨝B

PolarDB分布式版采用的Join Reorder算法为基于规则变换Top-Down的Join Reorder算法。
Duplicate Free Join Reorder Rule Set
Adaptive Search Space
| 表数目 | 搜索空间 |
| <= 4 | Bushy Tree |
| <= 6 | Zig-Zag Tree |
| <= 8 | Left Deep Tree |
| >=9 | Heuristic |
在表数>=9个的时候,PolarDB-X会采用多序列贪心启发式Join Reorder算法加速Join Reorder的过程。
Join Reorder与其他规则
索引选择规则:因为PolarDB分布式版支持全局二级索引,不同的全局二级索引会影响Join的下推和Join算法规则,因此这类规则也会和Join Reorder规则一起构成搜索空间。
Branch And Bound空间剪枝

ABC的三表Join如果按照最开始的顺序优化出来了A、B、C依次使用Index Nested Loop Join,计算出代价值例如是10,之后通过Join Reorder的规则构造出了B Join C但是我们看到B Join C的最低代价也要1000,因为是两张大表做Join,既然[ABC]等价集合中已经有了一个代价为10的执行计划。那么可以直接裁剪掉[BC]不再去为它们生成物理执行计划,因为它们无论选择什么物理执行计划都不会比10低。这就是Branch And Bound空间剪枝。
这里规则的应用顺序可以看出如果从上到下应用物理转换规则那我们有机会做到剪枝,不需要去搜索部分空间。一般来说会通过特定的启发式方法来指导搜索引擎应用物理转化规则,尽快找到一个代价低的执行计划,并利用其代价去进行空间剪枝。


PolarDB分布式版在表数据较多时(>=9)采用多序列贪心启发式Join Reorder算法。
PolarDB分布式版在表数目较少时(<9)采用基于规则变换的Top-Down的Join Reorder算法,它有如下的优点:
● 使用了Duplicate Free的Join Reorder规则提升Reorder效率;
● 通过Adaptive Search Space来控制搜索空间大小;
● 通过Join Reorder规则和Join算法规则、Join下推规则、Agg与Join交换规则、索引选择规则一起构建搜索空间,获取全局最优解;
参考文献
[1] https://db.in.tum.de/teaching/ws1415/queryopt/chapter3.pdf
[2] https://www.postgresql.org/docs/9.1/geqo-pg-intro.html
[3] Analysis of Two Existing and One New Dynamic Programming Algorithm for the Generation of Optimal Bushy Join Trees without Cross Products
[4] The Cascades Framework for Query Optimization
[5] On the Correct and Complete Enumeration of the Core Search Space
[6] Improving Join Reorderability with Compensation Operators
[7] The Complexity of Transformation-Based Join Enumeration
[8] Measuring the Complexity of Join Enumeration in Query Optimization
[9] eager aggregation and lazy aggregation
云原生数据库 PolarDB 分布式版开通免费试用啦!
阿里云推出“飞天免费试用计划”,面向国内1000万云上开发者,提供云产品免费试用。云原生数据库 PolarDB 分布式版现推出3个月【免费试用】,快来领取吧!
点击文末「阅读原文」即刻开启云上实践之旅!




点击阅读原文免费试用 云原生数据库PolarDB分布式版







