论文导读 | 图上的可达性问题

图谱学苑 2021-05-15

1924

编者按：

本文旨在尽量全面地呈现目前图上可达性问题研究的图景。首先对求解可达性问题的框架方法进行分类，随后以时间为脉络简要介绍每类的主要技术、列举对应的文献以供参考。

一、问题定义

在有向图G=(V,E)上，对任两个结点u,v∈V，若存在从u到v的路径，那么称v是由u可达的，记作u→v。

给定一张有向图G=(V,E)，一对结点u,v∈V，可达性问题即为判定是否有u→v的判定问题。

求解可达性问题的方法主要可分为两类：一类是基于索引的方法（Index-based approaches），另一类是不基于索引的方法（Index-free approaches）。前者起源于上世纪八十年代末，至今仍为可达性问题的主流方法；后者在理论研究中有较为丰富的历史，而在实用框架中为近年来兴起的新趋势。

二、基于索引的方法

可达性索引为进行查询前对图预计算所得的图上全部或部分可达性信息（全部可达性信息即任意点对之间是否可达的信息）的摘要。如无特殊说明，至今的可达性索引均是以从原图中提取出的有向无环图为基础计算所得，而非直接从原图计算得到。具体来说，这种有向无环图是通过将原有向图中的每个强连通分量压缩成一个超结点，若存在由一个强连通分量内的结点指向另一个强连通分量内的结点的边，则在对应的两个超结点间连边的方式得到的。这种对原有向图的压缩方式显然能够无损保存其可达性信息：两结点之间可达当且仅当它们所属的超结点之间可达。同时，这种方式能降低索引的空间开销，有向无环图的结构特性也使一些索引的建立更加容易，因此被广泛采用。

基于索引的方法又可以进一步分为三类：压缩传递闭包（Transitive Closure Compression）、两跳标签（2-Hop Labeling）和通用索引框架（Generic Indexing Frameworks）。以下将逐一介绍这三类方法。

（1）压缩传递闭包（Transitive Closure Compression）

传递闭包即为表达图上全部可达性信息的矩阵。此类方法旨在对传递闭包进行压缩。根据压缩是否无损（即可解压缩出完整的原信息），这类方法可进一步划分为无损压缩、有损压缩两类；进行可达性查询时，前者只需检查索引本身即可得到准确结果，而后者的索引可能出现单侧错误（假阳性或假阴性），为避免单侧错误，必要时需要发起经索引剪枝的图遍历以保证得到准确结果。根据具体使用的技术，这类方法又可进一步划分为Tree-Cover (Interval Labeling), Chain-Cover, Weak Dominance Drawing, Set-Containment Testing四类。这两个分类标准是彼此正交的，即运用每种技术的方法都可能存在无损和有损压缩两种情况。

（1.1）Tree-Cover

顾名思义，这类方法基于树结构对图上的可达性信息进行覆盖。首先需建立有向无环图的生成树（如果有向无环图分为多个连通分量，则建立其生成树森林，并将所有生成树挂接在虚拟根结点上）；然后基于对生成树的后序遍历赋予每个结点一个二维坐标[i, j]，其中j为当前结点在后序遍历中的序号，i为以当前结点为根的子树中最小的后序遍历序号。若将此二维坐标看作一个区间（这也是Tree-Cover的别名：Interval Labeling的由来），则如果结点u的区间包含结点v的区间，那么容易知道结点u在生成树中为结点v的祖先，有结点u到v可达。然而，逆命题并不成立：即使结点u到v可达，结点u的区间也可能不包含结点v的区间。这是由于有向无环图中可能存在未包含在生成树中的边，而包含这些边的路径并不能被生成树所表示。因此，Tree-Cover可能产生假阴性（即将可达点对判定为不可达）。无损压缩方法需要使用额外的数据结构记录未被生成树覆盖的可达性信息。

（1.2）Chain-Cover

这类方法基于链结构（即路径）对图上的可达性信息进行覆盖。首先需将有向无环图分解为一系列的链；然后赋予每个结点一个或多个二维坐标[i, j]，其中j为当前结点所在的链编号，i为当前结点在该链上的位置序号。链分解需要满足结点u到v可达当且仅当存在一条链包含u和v，且u为该链上v的后继。由于计算满足条件的最小链分解是NP难问题，启发式算法的时间复杂度仍然较高，因此近年来针对这类方法的研究进展较少。

（1.3）Weak Dominance Drawing

Weak Dominance Drawing为源自图可视化领域的一项技术，旨在将图中结点映射到几何空间的同时保留一定的结构信息。赋予每个结点一个d维坐标，其中每一维是当前结点在一轮拓扑排序中的序号。坐标的支配关系（Domination）定义为：若结点v坐标的每一维都大于或等于结点u坐标的对应维度，那么称结点v的坐标支配结点u的坐标。由拓扑排序的性质可知，若结点u可达结点v，则说明结点v在任一轮拓扑排序中都应位于结点u之后，则有结点v的坐标支配结点u的坐标。然而，由于索引规模受限，d一般显著小于所有可能的拓扑排序数量，因此结点v的坐标支配结点u的坐标仅是结点u可达结点v的必要非充分条件，Weak Dominance Drawing可能发生假阳性（即将不可达点对判定为可达）。一项能有效降低假阳性率的贪心策略是：从第二轮拓扑排序开始，对于在已有的排序中排名越靠前的结点，越尽量延后它在本轮中的出现。

（1.4）Set-Containment Testing

这类方法基于可达性的性质：若结点u可达结点v，则所有可达结点u的结点均可达结点v，所有从结点v可达的结点均从结点u可达。若将可达结点v的结点集合记作In(v)，将从结点v可达的结点集合记作Out(v)，则上述条件可抽象为两个集合包含关系检查：是否有In(u)⊆In(v)且Out(v)⊆Out(u). 若不满足这对关系，则从结点u到结点v一定不可达；但即使满足，也仍然存在结点u到结点v不可达的情况，即可能发生假阳性。

目前压缩传递闭包的方法中综合表现最优的即为一种使用了Set-Containment Testing技术的方法，它对每个结点的In(⋅),Out(⋅)集合进行Independent Permutation处理，并保留其k-min元素，在优化存储的同时提供了其假阳性率的理论上界，必要时仍然发起图遍历以保证结果准确。

（2）两跳标签（2-Hop Labeling）

两跳标签为将所有可达关系以两跳关系表示的一种方法。具体来说，赋予每个结点一对结点集合

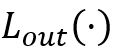与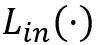

，使得结点u可达结点v当且仅当

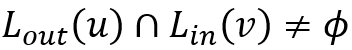. 在这对结点集合中、用于连接可达结点对的中介结点称为hop. 直观上，我们希望找到尽量少的hop来覆盖所有的可达点对。已有理论工作证明在具有某些结构特征的图上最小两跳标签的总空间上限为

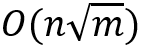, 其中n为总结点数，m为总边数；并猜想在任意图上两跳标签仍满足此性质。

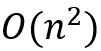将关于两跳标签的理论落实到实用方法框架中的开山之作是E. Cohen等人发表于2003年的工作“Reachability and Distance Queries via 2-Hop Labels.”他们证明了计算最小两跳标签是一个NP难问题，并给出了一个多项式时间（时间复杂度为

）的贪心算法，可得出空间占用在理论最小值的

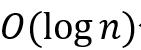倍之内的两跳标签。这个算法首先需要计算和暂存图的传递闭包，然后对每对可达结点维护一个最大堆，以每个hop能覆盖的它们之间的近似路径比例为键值，每次取堆顶元素放入标签中。

上述工作为两跳标签在可达性算法框架中的实际运用奠定了良好基础。它提供的索引建立算法对索引的空间占用具有确定的理论保证，但时间和空间开销都相当大：一是因为要计算和在内存中暂存整个传递闭包；二是维护最大堆和重新计算键值的时间开销也比较大。因此后续许多跟进工作聚焦于改进索引建立的算法，降低开销。其中一类方法使用分治策略，先将原图分割成数个子图，分别计算每个子图的两跳标签，最终再合并所有标签并加入仅能由跨子图的边所覆盖的可达性信息，从而避免计算和存储原图的完整传递闭包；另一类方法从外部确定加入hop的顺序，主要分拓扑顺序与启发式顺序两种，从而避免最大堆的维护开销。目前两跳标签中综合表现最优的方法即将当时已有的基于外部顺序的方法归纳于统一框架下，并在此基础上提出了新的成本函数，从而开发一种新的启发式顺序，在静态图上表现优于此前方法的基础上对动态图也进行优化。上述两类方法都能有效降低建索引过程中的时间和空间开销，但所得到的两跳索引不再具备空间占用的理论上界保证。

另有一类两跳标签的后续工作仍不满足于初始给出的索引空间占用保证，希望在更稠密的图上得到更节省空间的索引。在经典的两跳标签中，hop被定义为连接可达点对的中介结点。这类工作不再使用结点作为可达点对的中介，而是将其扩展为图的子结构；直观上，一个大于结点的子结构可以覆盖更多的可达点对，从而降低索引的空间需求。目前的两篇工作分别将两跳索引与Chain-cover和Tree-Cover相结合，将链或子树作为连接可达点对的中介。这样得到的索引占用空间更小，但建索引所需的时间开销更大。

值得一提的还有今年由Q. Lyu等发表的“DBL: Efficient Reachability Queries on Dynamic Graphs”。不同于此前基于索引的工作以静态图为主、仅将支持动态图作为扩展，这一工作将在动态图上的高效可达性查询和索引更新作为其主要贡献，这也契合了近年来动态图数量和规模逐渐增加的趋势。由于原图的有向无环图在图更新触发强连通分量的分裂或融合时需要比查询高数量级以上的维护时间开销，因此本作采用直接在原图上建索引，而不再维护有向无环图。因原图规模更大，且还需支持索引在图更新时的高效维护，所以其索引非常轻量化，分为两部分：一是两跳标签的子集，仅将预先选定的常数个高度数结点（称为路标，Landmark）作为hop加入到索引集合中；二是Set-Containment Testing索引的子集，仅将预先选定的低度数结点（称为叶结点，Leaf）加入到索引集合中。两跳标签原本能够准确回答任何可达性查询，但在取子集后可能发生假阴性；而Set-Containment Testing可能发生假阳性，两个索引分别优化答案为真的查询和答案为假的查询，发挥互补作用，有较好的查询性能，在动态图上取得了目前为止的最优表现。

（3）通用索引框架（Generic Indexing Frameworks）

通用索引框架是与前两类相互正交的一类方法。其出发点为不同的图具有迥异的结构，虽然针对某种特定结构的图往往有高性能的索引，但难以找到一种索引适应所有结构的图。因此，可以考虑对图进行分割，对不同结构的子图选用不同的索引，再给出合并不同索引给出的答案得出最终查询结果的算法。研究重点即为如何对图进行合理的分割、如何合理分配索引。

三、不基于索引的方法

不基于索引的方法主要的设计目标有二：一是基于目前的可达性索引更新效率仍然较低的现实，希望通过去除索引为动态图提供更优的支持；二是基于建立所有可能出现的约束所对应的特化可达性索引（前文未介绍）时间与空间开销过大的现实，希望适应随机出现的查询约束的需求。

最简单的不基于索引的方法即为图遍历。自上世纪九十年代以来，理论研究中出现基于随机游走的可达性算法，其基本思路为从源结点、目标结点分别发起前向、后向随机游走，若来自两个方向的随机游走访问了相同结点，则返回真，否则返回假。这显然是一种近似算法，可能出现假阴性，因为随机游走不一定能够恰好覆盖连接可达点对的路径。理论研究中通过控制随机游走的数量、长度等参数，为假阴性率提供理论上界。这类方法天然地能够支持动态图和随机查询约束（只需在发起随机游走时施加约束即可）。N. Sengupta等发表于2019年的“ARROW: Approximating Reachability Using Random Walks Over Web-Scale Graphs”为这一思路提供了可用于真实图的实现，但其实际查询性能在不同图上差距较大，并不保证优于图遍历。性能更优的不基于索引的方法还有待开发。

四、总结

本文给出了图上可达性的问题定义，并以是否基于索引为分类标准，总结了迄今为止求解图上可达性问题方法的主要技术路线、简要介绍了每种技术对应的重要工作。

参考文献

[1] A. Anagnostopoulos, R. Kumar, M. Mahdian, E.Upfal, and F. Vandin, “Algorithms on evolving graphs,” in Proceedings of the 3rd Innovations in Theoretical ComputerScience Conference on - ITCS ’12, Cambridge, Massachusetts, 2012, pp. 149–160, doi: 10.1145/2090236.2090249.

[2] A. D. Zhu, W. Lin, S. Wang, and X. Xiao, “Reachability queries on large dynamic graphs: a totalorder approach,” in Proceedings ofthe 2014 ACM SIGMOD International Conference on Management of Data,Snowbird Utah USA, Jun. 2014, pp. 1323–1334, doi: 10.1145/2588555.2612181.

[3] E. Cohen, E. Halperin, H. Kaplan, and U. Zwick, “Reachability and Distance Queries via 2-Hop Labels,” SIAM J. Comput., vol. 32, no. 5, pp. 1338–1355, Jan. 2003, doi: 10.1137/S0097539702403098.

[4] Haixun Wang, Hao He, Jun Yang, P. S. Yu, and J. X.Yu, “Dual Labeling:Answering Graph Reachability Queries in Constant Time,” in 22nd International Conference on DataEngineering (ICDE’06), Atlanta, GA, USA, 2006, pp. 75–75, doi: 10.1109/ICDE.2006.53.

[5] H. He, H. Wang, J. Yang, and P. S. Yu, “Compact reachability labeling for graph-structureddata,” in Proceedings ofthe 14th ACM international conference on Information and knowledge management -CIKM ’05, Bremen, Germany,2005, p. 594, doi: 10.1145/1099554.1099708.

[6] H. V. Jagadish, “A compression technique to materialize transitiveclosure,” ACM Trans.Database Syst., vol. 15, no. 4, pp. 558–598, Dec. 1990, doi: 10.1145/99935.99944.

[7] H. Wei, J. X. Yu, C. Lu, and R. Jin, “Reachability querying: an independent permutationlabeling approach,” Proc. VLDB Endow.,vol. 7, no. 12, pp. 1191–1202, Aug. 2014, doi: 10.14778/2732977.2732992.

[8] H. Wei, J. X. Yu, C. Lu, and R. Jin, “Reachability querying: an independent permutationlabeling approach,” The VLDB Journal,vol. 27, no. 1, pp. 1–26, Feb. 2018, doi: 10.1007/s00778-017-0468-3.

[9] H. Yildirim, V. Chaoji, and M. J. Zaki, “DAGGER: A Scalable Index for Reachability Queries inLarge Dynamic Graphs,” arXiv:1301.0977 [cs], Jan. 2013, Accessed: Mar. 20, 2021.[Online]. Available: http://arxiv.org/abs/1301.0977.

[10] H. Yıldırım, V. Chaoji, and M. J. Zaki, “GRAIL: a scalable index for reachability queries invery large graphs,” The VLDB Journal,vol. 21, no. 4, pp. 509–534, Aug. 2012, doi: 10.1007/s00778-011-0256-4.

[11] H. Yildirim, V. Chaoji, and M. J.Zaki, “GRAIL: scalable reachability index for large graphs,” Proc. VLDBEndow., vol. 3, no. 1–2, pp. 276–284, Sep. 2010, doi: 10.14778/1920841.1920879.

[12] J. Cai and C. K. Poon, “Path-hop:efficiently indexing large graphs for reachability queries,” in Proceedingsof the 19th ACM international conference on Information and knowledgemanagement - CIKM ’10, Toronto, ON, Canada, 2010, p. 119, doi: 10.1145/1871437.1871457.

[13] J. Cheng, J. X. Yu, X. Lin, H. Wang,and P. S. Yu, “Fast Computation of Reachability Labeling for Large Graphs,” in Advancesin Database Technology - EDBT 2006, vol. 3896, Y. Ioannidis, M. H. Scholl,J. W. Schmidt, F. Matthes, M. Hatzopoulos, K. Boehm, A. Kemper, T. Grust, andC. Boehm, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2006, pp.961–979.

[14] J. Cheng, J. X. Yu, X. Lin, H. Wang,and P. S. Yu, “Fast computing reachability labelings for large graphs with highcompression rate,” in Proceedings of the 11th international conference onExtending database technology Advances in database technology - EDBT ’08,Nantes, France, 2008, p. 193, doi: 10.1145/1353343.1353370.

[15] J. Cheng, S. Huang, H. Wu, and A.W.-C. Fu, “TF-Label: a topological-folding labeling scheme for reachabilityquerying in a large graph,” in Proceedings of the 2013 internationalconference on Management of data - SIGMOD ’13, New York, New York, USA,2013, p. 193, doi: 10.1145/2463676.2465286.

[16] J. Su, Q. Zhu, H. Wei, and J. X. Yu,“Reachability Querying: Can It Be Even Faster?,” IEEE Trans. Knowl. DataEng., vol. 29, no. 3, pp. 683–697, Mar. 2017, doi: 10.1109/TKDE.2016.2631160.

[17] L. Chen, A. Gupta, and M. E. Kurul,“Stack-based Algorithms for Pattern Matching on DAGs,” p. 12, 2005.

[18] L. Li, W. Hua, and X. Zhou, “HD-GDD:high dimensional graph dominance drawing approach for reachability query,” WorldWide Web, vol. 20, no. 4, pp. 677–696, Jul. 2017, doi: 10.1007/s11280-016-0407-z.

[19] L. Roditty and U. Zwick, “ImprovedDynamic Reachability Algorithms for Directed Graphs,” SIAM J. Comput.,vol. 37, no. 5, pp. 1455–1471, Jan. 2008, doi: 10.1137/060650271.

[20] L. Zhu, B. Choi, B. He, J. X. Yu, andW. K. Ng, “A Uniform Framework for Ad-Hoc Indexes to Answer ReachabilityQueries on Large Graphs,” in Database Systems for Advanced Applications,vol. 5463, X. Zhou, H. Yokota, K. Deng, and Q. Liu, Eds. Berlin, Heidelberg:Springer Berlin Heidelberg, 2009, pp. 138–152.

[21] M. Starnini, A. Baronchelli, A.Barrat, and R. Pastor-Satorras, “Random walks on temporal networks,” Phys.Rev. E, vol. 85, no. 5, p. 056115, May 2012, doi: 10.1103/PhysRevE.85.056115.

[22] N. Sengupta, A. Bagchi, M. Ramanath,and S. Bedathur, “ARROW: Approximating Reachability Using Random Walks OverWeb-Scale Graphs,” in 2019 IEEE 35th International Conference on DataEngineering (ICDE), Macao, Macao, Apr. 2019, pp. 470–481, doi: 10.1109/ICDE.2019.00049.

[23] Q. Lyu, Y. Li, B. He, and B. Gong,“DBL: Efficient Reachability Queries on Dynamic Graphs (Complete Version),”arXiv:2101.09441 [cs], Jan. 2021, Accessed: Mar. 24, 2021. [Online]. Available:http://arxiv.org/abs/2101.09441.

[24] R. Agrawal, A. Borgida, and H. V.Jagadish, “Efficient management of transitive relationships in large data andknowledge bases,” in Proceedings of the 1989 ACM SIGMOD internationalconference on Management of data - SIGMOD ’89, Portland, Oregon, UnitedStates, 1989, pp. 253–262, doi: 10.1145/67544.66950.

[25] R. Jin and G. Wang, “Simple, fast, andscalable reachability oracle,” Proc. VLDB Endow., vol. 6, no. 14, pp.1978–1989, Sep. 2013, doi: 10.14778/2556549.2556578.

[26] R. Jin, N. Ruan, S. Dey, and J. Y. Xu,“SCARAB: scaling reachability computation on large graphs,” in Proceedingsof the 2012 international conference on Management of Data - SIGMOD ’12,Scottsdale, Arizona, USA, 2012, p. 169, doi: 10.1145/2213836.2213856.

[27] R. Jin, N. Ruan, Y. Xiang, and H. Wang,“Path-tree: An efficient reachability indexing scheme for large directedgraphs,” ACM Trans. Database Syst., vol. 36, no. 1, pp. 1–44, Mar. 2011,doi: 10.1145/1929934.1929941.

[28] R. Jin, Y. Xiang, N. Ruan, and H.Wang, “Efficiently answering reachability queries on very large directedgraphs,” in Proceedings of the 2008 ACM SIGMOD international conference onManagement of data - SIGMOD ’08, Vancouver, Canada, 2008, p. 595, doi: 10.1145/1376616.1376677.

[29] R. Jin, Y. Xiang, N. Ruan, and D.Fuhry, “3-HOP: a high-compression indexing scheme for reachability query,” in Proceedingsof the 35th SIGMOD international conference on Management of data - SIGMOD ’09,Providence, Rhode Island, USA, 2009, p. 813, doi: 10.1145/1559845.1559930.

[30] R. R. Veloso, L. Cerf, W. M. Junior,and M. J. Zaki, “Reachability Queries in Very Large Graphs: A Fast RefinedOnline Search Approach.” OpenProceedings.org, 2014, doi: 10.5441/002/EDBT.2014.46.

[31] R. Schenkel, A. Theobald, and G.Weikum, “Efficient Creation and Incremental Maintenance of the HOPI Index forComplex XML Document Collections,” in 21st International Conference on DataEngineering (ICDE’05), Tokyo, Japan, 2005, pp. 360–371, doi: 10.1109/ICDE.2005.57.

[32] R. Schenkel, A. Theobald, and G.Weikum, “HOPI: An Efficient Connection Index for Complex XML DocumentCollections,” in Advances in Database Technology - EDBT 2004, vol. 2992,E. Bertino, S. Christodoulakis, D. Plexousakis, V. Christophides, M.Koubarakis, K. Böhm, and E. Ferrari, Eds. Berlin, Heidelberg: Springer BerlinHeidelberg, 2004, pp. 237–255.

[33] S. J. van Schaik and O. de Moor, “Amemory efficient reachability data structure through bit vector compression,”in Proceedings of the 2011 international conference on Management of data -SIGMOD ’11, Athens, Greece, 2011, p. 913, doi: 10.1145/1989323.1989419.

[34] S. Seufert, A. Anand, S. Bedathur, andG. Weikum, “FERRARI: Flexible and efficient reachability range assignment forgraph indexing,” in 2013 IEEE 29th International Conference on DataEngineering (ICDE), Brisbane, QLD, Apr. 2013, pp. 1009–1020, doi: 10.1109/ICDE.2013.6544893.

[35] S. Trißl and U. Leser, “Fast andpractical indexing and querying of very large graphs,” in Proceedings of the2007 ACM SIGMOD international conference on Management of data - SIGMOD ’07,Beijing, China, 2007, p. 845, doi: 10.1145/1247480.1247573.

[36] S. Zhou, P. Yuan, L. Liu, and H. Jin,“MGTag: a Multi-Dimensional Graph Labeling Scheme for Fast ReachabilityQueries,” in 2018 IEEE 34th International Conference on Data Engineering(ICDE), Paris, Apr. 2018, pp. 1372–1375, doi: 10.1109/ICDE.2018.00153.

[37] U. Feige, “A fast randomized LOGSPACEalgorithm for graph connectivity,” Theoretical Computer Science, vol. 169,no. 2, pp. 147–160, Dec. 1996, doi: 10.1016/S0304-3975(96)00118-1.

[38] Y. Chen and Y. Chen, “An EfficientAlgorithm for Answering Graph Reachability Queries,” in 2008 IEEE 24thInternational Conference on Data Engineering, Cancun, Mexico, Apr. 2008,pp. 893–902, doi: 10.1109/ICDE.2008.4497498.

[39] Y. Yano, T. Akiba, Y. Iwata, and Y.Yoshida, “Fast and scalable reachability queries on graphs by pruned labelingwith landmarks and paths,” in Proceedings of the 22nd ACM internationalconference on Conference on information & knowledge management - CIKM ’13,San Francisco, California, USA, 2013, pp. 1601–1606, doi: 10.1145/2505515.2505724.

相关链接

论文导读 | 知识图谱质量控制

论文导读 | 神经网络优化的图编辑距离计算

论文导读 | 图生成模型综述

论文导读 | 加速GPU上的三角形计数算法

论文导读 | 滑动窗口模型下含重复边的图流上的三角形近似计数算法

讲座录播及课件｜Tamer Özsu教授：分布式RDF数据管理和SPARQL查询处理

图数据库系统gStore v0.9适配鲲鹏920服务器教程北京大学重庆大数据研究院招聘图数据库与知识图谱系统研发和工程人员（含新增职位）

数据库 gstore

文章转载自图谱学苑，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

论文导读 | 图上的可达性问题

评论