数据库集合运算与关系代数

一：域　　　　　　

　　具有一组相同类型的数据集合。

二:笛卡尔积　　　

　　域上定义的一种集合运算,就是将每个域中的元素与其它域中的元素分别去组合,组合得到的笛卡尔积中每一个元素叫做一个元组。如图，是D1和D2的笛卡尔积。

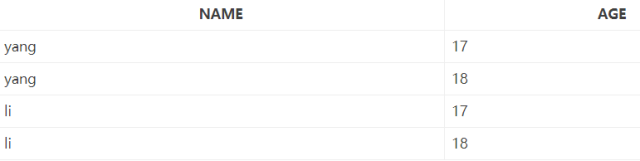
三:关系　　　　　

　　在笛卡尔积中取出一个子集，可以构成关系。关系中的每个元素是关系中的元组,关系是笛卡尔积的真子集。

　　在D1XD2中取出来一个关系如下图所示,关系才是有意义的。

四:键　　　　　　

　　1.候选键：某个能唯一标识一个元组的属性值或者域称为候选键。

　　2.主键：从候选键中选出一个键成为主键。

　　3.全键：所有的属性组或者域是这个元组的候选键，我们叫全键。

　　4.外键：Y是R关系中的属性组，但不是R关系中的主键，但是是S关系中的主键，此时Y就叫做R关系的外键。

五:三条完整性规则

　　1.实体完整性:若属性A是关系R的主属性，则A不能取空值。

　　2.参照完整性：回忆外键的定义，若F是关系R的外键，它与关系S主键相对应，对于R中的每个元组在F上的取值，要么等于S中的主键值，要么为空 。

　　3.用户定义的完整性:任何数据库都应该支持实体完整性和参照完整性，并且对于不同的应用我们应该加一些别的约束条件。

六:关系代数　　　

1.并，差，交 按照我们普通的集合运算的方式理解就好了。

2.笛卡尔积也是这样的一种操作，m元关系就是有m个域。m元关系和n元关系进行笛卡尔积得到(m+n)元关系。

3.选择：选出在关系R中满足给定条件的诸元组。

4.投影：选出列组成新的关系，会指定选择的列号和集合名称。

5.连接：从两个关系的笛卡尔积中选取属性间满足一定条件的元组。

　　自然连接:自然连接是特殊的等值连接，它会去掉相同的属性组。

　　等值连接:条件是从R和S的笛卡尔积中选取A，B属性值相等的元组。

　　外连接：把应该舍弃的全部保留下来，在其他对应属性上用null。

6.除：对于两个关系R(X,Y)和S(Y,Z)，R/S得到的。是R在X上满足下面条件的投影，条件是：元素在X分量上x的象集包括S在Y投影上的集合。

　　有关象集的定义在下面:

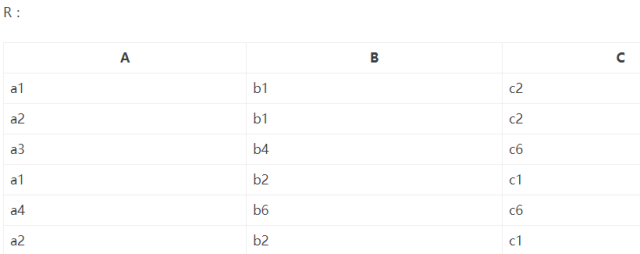
　　X的象集是针对R中x的每一个取值而言的：实际上就是对应Y关系上的取值，X关系是A,Y关系是B和C。

　　找到了X分量上x的象集，我们继续找S在Y投影上的集和，在S关系中，S在Y关系上（也就是B和C关系上）的投影为：

　　下面我们只用x的象集和S在Y关系上的投影（{（b1,c2）（b2,c1）}）进行对比就行了，发现只有a1和a2的象集包含这个投影，也就是R/S= {a1,a2}

　　现在我们会计算除法了，它到底有什么意义：除的意义在于查询全部，就像我们的a的象集中完全包括S在Y关系上的投影的a的值才能被选出来，它们是完全符合S元素的。