赛题 1：找出各项考试中的佼佼者

1. 解题思路

1. 先找出各科成绩排名第三的成绩
2. 查询各科成绩高于或等于第三的名单
3. 关联student，test表，获取学生姓名和科目的名称

2. sql语句如下：

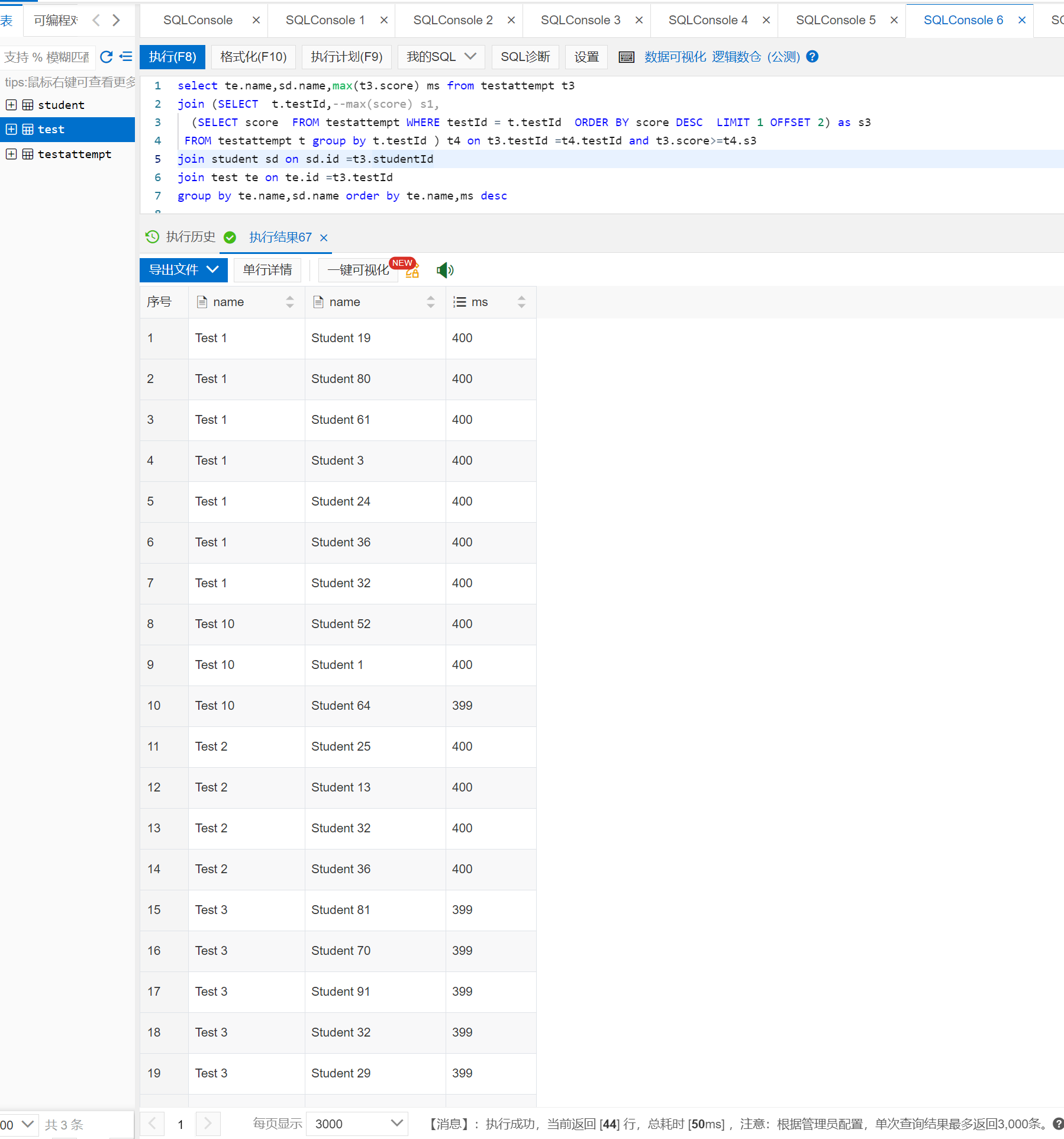
select te.name,sd.name,max(t3.score) ms from testattempt t3
join (SELECT  t.testId,--max(score) s1,
  (SELECT score  FROM testattempt WHERE testId = t.testId  ORDER BY score DESC  LIMIT 1 OFFSET 2) as s3
 FROM testattempt t group by t.testId ) t4 on t3.testId =t4.testId and t3.score>=t4.s3
join student sd on sd.id =t3.studentId
join test te on te.id =t3.testId
group by te.name,sd.name order by te.name,ms desc

3. 增加索引提速

create index idx_testattempt_test_s on testattempt(testId,scope);
create index idx_testattempt_st  on testattempt(studentId);

-- 这2个索引也可以不创建，有主键
create index idx_test_Id_s on test(id);
create index idx_student_id on student(id);

4. 优化表：成绩表导入大量数据

OPTIMIZE TABLE `testattempt`;

5. 执行结果和耗时如下（由于展示原因截图不全）

赛题 2：游戏游玩情况

编写一个 SQL 查询，报告在首次游玩后的一周内至少再有一次游玩的玩家的比例，也就是注册首周内至少有两次登录的玩家占总玩家的比例，四舍五入到小数点后两位

1. 解题思路

1. 获取玩家第一次和第二次登录时间
2. 比较第二次与第一次是时间是否为7天
3. 统计7天内登录的玩家占比

2. sql语句

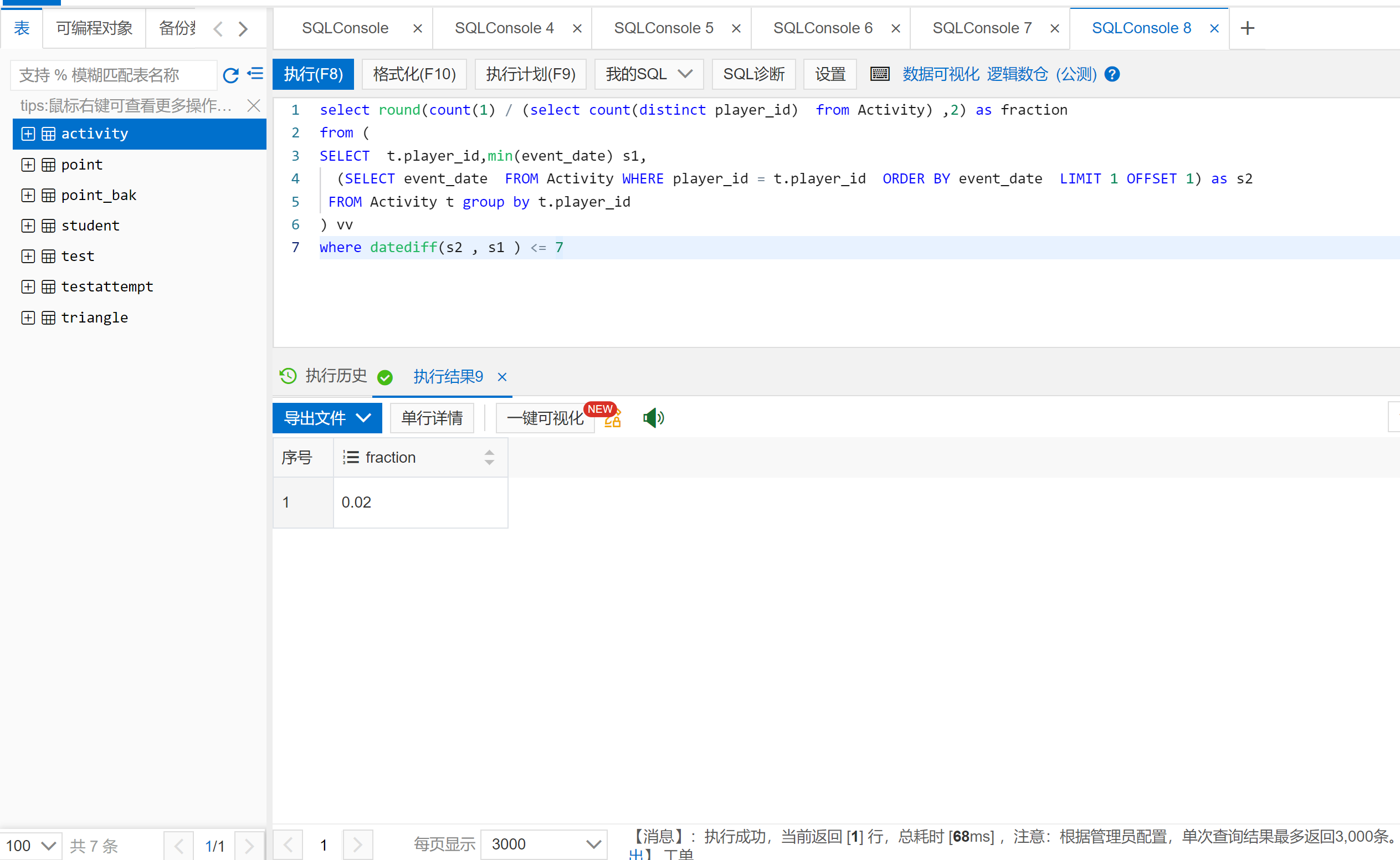
select round(count(1) / (select count(distinct player_id)  from Activity) ,2) as fraction
from (
SELECT  t.player_id,min(event_date) s1,
  (SELECT event_date  FROM Activity WHERE player_id = t.player_id  ORDER BY event_date  LIMIT 1 OFFSET 1) as s2
 FROM Activity t group by t.player_id 
) vv
where datediff(s2 , s1 ) <= 7

3. 增加索引

create index idx_activity_d on Activity(event_date);

4. 执行结果及耗时

赛题 3：计算三角形面积

要求：计算每个三角形的面积，保留两位小数

1. 解题思路

1. 根据向量积的模的几何意义，求三角形的面积
2. 首先计算出三角形相邻2条边的向量
3. 使用上述得到的2个向量，计算出向量积
4. 三角形的面积等于1/2 乘于向量积的模

2. 优化处理

1）. 增加索引

create index idx_triangle_pointId1 on Triangle(pointId1,pointId2,pointId3)

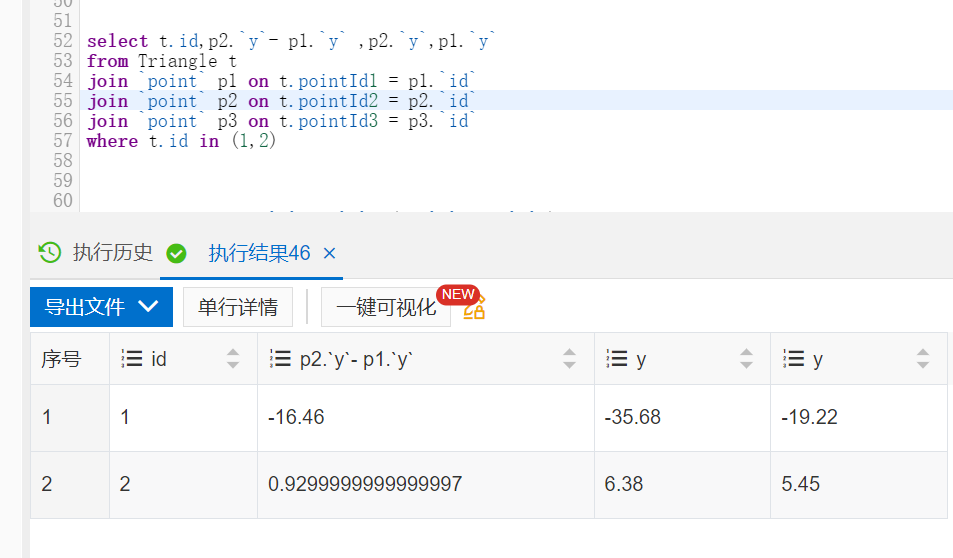
2）.鉴于DOUBLE类型计算结果不准确（如图），将point的字段更改为DECIMAL

-- 创建表
CREATE TABLE Point_new (
    id INT PRIMARY KEY,
    x DECIMAL(4,2) ,
    y DECIMAL(4,2),
    z DECIMAL(4,2)
);
-- 插入数据
insert into Point_new select * from Point

-- 新旧表替换
alter table  Point rename  Point_bak;
alter table  Point_new rename  Point;

3. 查询三角形面积的SQL（设定保留2位小数）

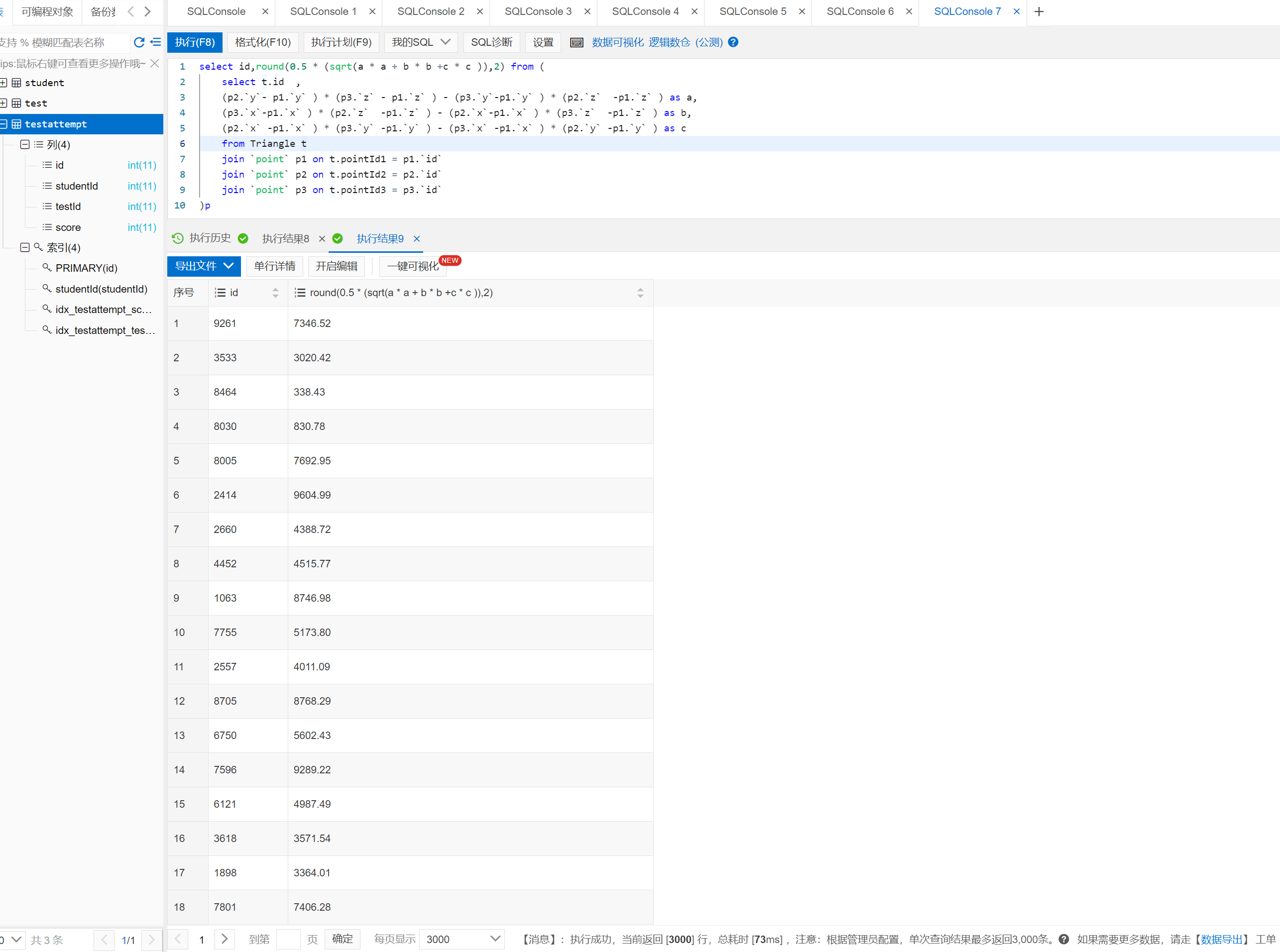
select id,round(0.5 * (sqrt(a * a + b * b +c * c )),2) from (
    select t.id  ,
    (p2.`y`- p1.`y` ) * (p3.`z` - p1.`z` ) - (p3.`y`-p1.`y` ) * (p2.`z`  -p1.`z` ) as a, 
    (p3.`x`-p1.`x` ) * (p2.`z`  -p1.`z` ) - (p2.`x`-p1.`x` ) * (p3.`z`  -p1.`z` ) as b,
    (p2.`x` -p1.`x` ) * (p3.`y` -p1.`y` ) - (p3.`x` -p1.`x` ) * (p2.`y` -p1.`y` ) as c
    from Triangle t
    join `point` p1 on t.pointId1 = p1.`id` 
    join `point` p2 on t.pointId2 = p2.`id`
    join `point` p3 on t.pointId3 = p3.`id`
)p

4. 执行结果及耗时

PS：配图纯数学，解题思路之一