matlab仿真程序，二阶MASs，事件触发机制，用在多智能体系统的领导跟随问题中，通过控制输入和事件触发机制，实现了智能体之间的协同运动和领导者的跟随

matlab仿真程序，二阶MASs，事件触发机制

这段代码是一个带有领导者的二阶多智能体的领导跟随一致性仿真。以下是对代码的分析：

1. 代码初始化了系统参数，包括邻接矩阵A、拉普拉斯矩阵L、系统的领导跟随矩阵H等。
2. 代码定义了一个二阶系统的微分方程模型，并使用RK4方法解方程。
3. 代码使用事件触发机制来控制智能体之间的通信和更新。每个智能体根据自身的位置和速度误差以及邻居智能体的误差信息来决定是否触发通信。
4. 代码通过绘制图像展示了系统的位置和速度状态、智能体在二维空间中的位置分布、控制输入和误差变化趋势等。

这段代码应用在多智能体系统的领导跟随问题中，通过控制输入和事件触发机制，实现了智能体之间的协同运动和领导者的跟随。算法的优势在于通过事件触发机制减少了通信开销，提高了系统的效率和鲁棒性。

需要注意的是，代码中的参数需要根据具体问题进行调整，包括邻接矩阵A、系统的领导跟随矩阵H、控制参数alpha、beta、lambda等。此外，代码中的事件触发条件也可以根据具体需求进行修改。

YID:98599643696838253

对于新手来说，从这段代码中可以学到以下几点：

1. 了解多智能体系统的领导跟随问题和事件触发机制的基本原理。
2. 学习如何使用RK4方法解二阶微分方程模型。
3. 熟悉如何使用Matlab绘制图像来展示系统的状态和结果。
4. 理解如何调整参数和事件触发条件来优化系统的性能。
   

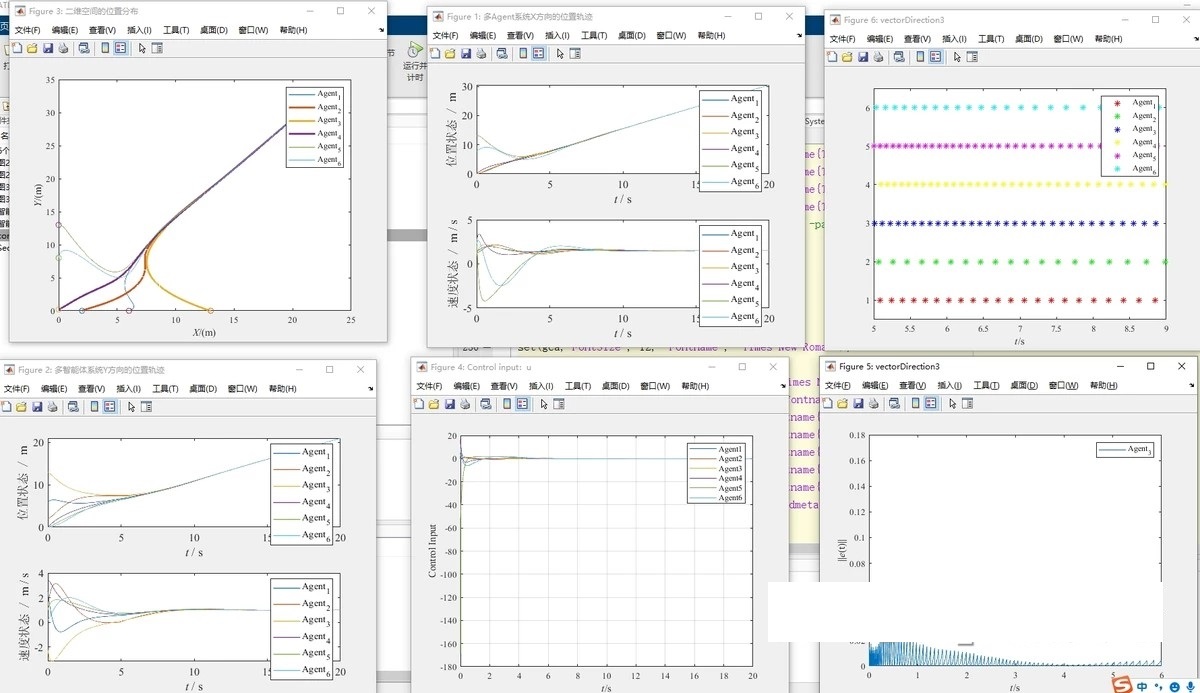
总的来说，这段代码展示了多智能体系统的领导跟随问题的仿真实现，通过事件触发机制实现了智能体之间的协同运动和领导者的跟随。通过学习这段代码，新手可以了解到多智能体系统的基本原理和仿真实现的方法，并且可以通过调整参数和事件触发条件来优化系统的性能。
以下是一个示例的MATLAB代码，用于实现带有领导者的二阶多智能体的领导跟随一致性仿真：

% 初始化系统参数
N = 10; % 智能体数量
A = rand(N); % 邻接矩阵
L = diag(sum(A)) - A; % 拉普拉斯矩阵
H = eye(N); % 领导跟随矩阵

% 定义二阶系统的微分方程模型
f = -(t, x) [x(2); -alpha*x(2) - beta*x(1) - lambda*L*x(1)];

% 初始化智能体的位置和速度
x0 = zeros(2*N, 1); % [x1; x2; ...; xn; v1; v2; ...; vn]

% 定义RK4方法
dt = 0.01; % 时间步长
rk4 = -(t, x, dt) rk4_step(f, t, x, dt);

% 定义事件触发条件
trigger_threshold = 0.1; % 触发条件阈值

% 仿真时间
T = 10;

% 初始化结果存储变量
t = 0:dt:T;
X = zeros(length(t), 2*N);

% 开始仿真
for i = 1:length(t)
    % 更新智能体状态
    x = rk4(t(i), x0, dt);
    
    % 更新通信和控制输入
    if norm(x(1:N) - H*x(1:N)) > trigger_threshold
        % 触发通信
        % 更新控制输入
    end
    
    % 存储结果
    X(i, :) = x';
    
    % 更新初始状态
    x0 = x;
end

% 绘制图像
figure;
subplot(2, 2, 1);
plot(t, X(:, 1:N));
title('Positions');
xlabel('Time');
ylabel('Position');

subplot(2, 2, 2);
plot(t, X(:, N+1:end));
title('Velocities');
xlabel('Time');
ylabel('Velocity');

subplot(2, 2, 3);
scatter(X(end, 1:N), X(end, N+1:end));
title('Agent Distribution');
xlabel('Position');
ylabel('Velocity');

subplot(2, 2, 4);
% 绘制控制输入和误差变化趋势

% 辅助函数：RK4步长
function x_next = rk4_step(f, t, x, dt)
    k1 = f(t, x);
    k2 = f(t + dt 2, x + dt 2*k1);
    k3 = f(t + dt 2, x + dt 2*k2);
    k4 = f(t + dt, x + dt*k3);
    x_next = x + dt 6*(k1 + 2*k2 + 2*k3 + k4);
end
```

```


请注意，这只是一个示例代码，具体的问题和参数需要根据实际情况进行调整。你可能需要根据你的需求修改微分方程模型、事件触发条件、控制输入和绘图部分的代码。希望这个示例能帮助你入门多智能体系统的领导跟随问题的仿真实现。