python之图像仿射变换实战-提取手写数字图片样本

做一个柔情的程序猿 2020-09-11

581

点击上方“蓝字”关注我，干货不断哦！

ython之图像仿射变换实战-提取手写数字图片样本

前言

这次梳理的篇幅主要是涉及图像仿射变换的一个实际应用，利用python编程实现提取手写数字图片样本，对巩固自己的python知识也是很有帮助的，进一步的对图像处理的内容也是帮助很大的。

但更多的是抛砖引玉，希望对你们有所帮助。

感谢各位鼓励与支持🌹🌹🌹，往期文章都在最后梳理出来了(●'◡'●)

接下来就以问题的形式展开梳理👇

连通域的外界矩形

在进行实战项目之前，我们先来学习一个知识点：连通域的外界矩形

寻找外接矩形有两种策略：最小外接

一种是寻找轮廓边缘的部分, 找到最外面的那个外接矩形, 为了区分, 我们称之为正外接矩形 boundingRect, 如下图绿色矩形部分.
另外一种策略是矩形可以旋转, 找到面积最小的矩形, 刚刚好可以把轮廓套在里面,我们称之为*最小外接矩形 * minAreaRect, 如下图蓝色矩形部分.

正外接矩形boudningRect

打印矩形区域信息

函数比较简单, 传入唯一的参数是轮廓点集(单个) Points
.👇

rect = cv2.boundingRect(cnt)
(x, y, w, h) = rect

返回值 rect
, 数据结构是tuple
, 分别为矩形左上角坐标(x, y)
, 与矩形的宽度w
高度h

我们依次打印矩形区域的信息.👇

for cidx,cnt in enumerate(contours):
    (x, y, w, h) = cv2.boundingRect(cnt)
    print('RECT: x={}, y={}, w={}, h={}'.format(x, y, w, h))

打印结果如下：👇

RECT: x=92, y=378, w=94, h=64
RECT: x=381, y=328, w=69, h=102
RECT: x=234, y=265, w=86, h=70
RECT: x=53, y=260, w=61, h=95
RECT: x=420, y=184, w=49, h=66
RECT: x=65, y=124, w=48, h=83
RECT: x=281, y=71, w=70, h=108

画布绘制具体代码

绘制在画布上比较直观，具体代码如下：👇

import numpy as np
import cv2

# 读入黑背景下的彩色手写数字
img = cv2.imread("color_number_handwriting.png")
# 转换为gray灰度图
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 寻找轮廓
contours, hier = cv2.findContours(gray, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

# 声明画布 拷贝自img
canvas = np.copy(img)

for cidx,cnt in enumerate(contours):
    (x, y, w, h) = cv2.boundingRect(cnt)
    print('RECT: x={}, y={}, w={}, h={}'.format(x, y, w, h))
    # 原图绘制圆形
    cv2.rectangle(canvas, pt1=(x, y), pt2=(x+w, y+h),color=(255, 255, 255), thickness=3)
    # 截取ROI图像
    cv2.imwrite("number_boudingrect_cidx_{}.png".format(cidx), img[y:y+h, x:x+w])

cv2.imwrite("number_boundingrect_canvas.png", canvas)

原始图像：👇

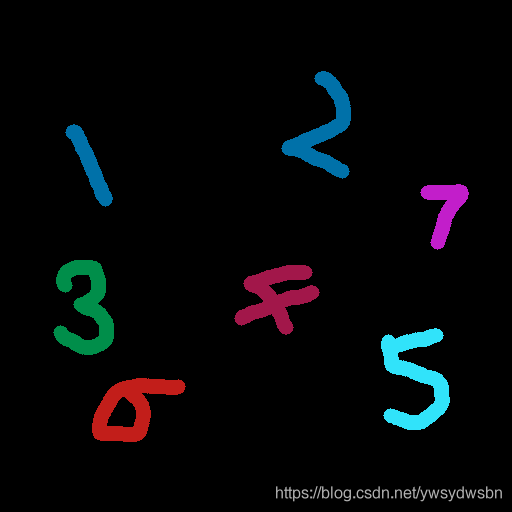
绘制结果如下：👇

截取ROI图片操作

截取ROI图片的操作比较简单img[y:y+h, x:x+w]
：👇

# 截取ROI图像
cv2.imwrite("number_boudingrect_cidx_{}.png".format(cidx), img[y:y+h, x:x+w])

这样我们就截取到了独立的单个数字的图片：👇

最小外接矩形minAreaRect

获取最小面积的矩形

minAreaRect
函数用于获取最小面积的矩形:👇

minAreaRect = cv2.minAreaRect(cnt)

我们打印一下minAreaRect
查看其返回的数据结构:

((133.10528564453125, 404.7727966308594), (100.10702514648438, 57.51853942871094), -49.184913635253906)

数据结构解析：

((cx, cy), (width, height), theta)

cx
矩形中心点x坐标 center x
cy
矩形中心点y坐标 center y
width
矩形宽度
height
矩形高度
theta
旋转角度，角度（不是弧度）

注意: 上述值均为小数, 不可以直接用于图片索引,或者矩形绘制.

详情见图：

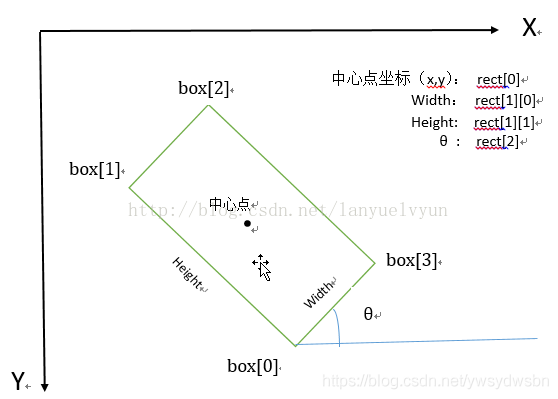
图片来源：python opencv minAreaRect 生成最小外接矩形
http://blog.csdn.net/lanyuelvyun/article/details/76614872

注意：旋转角度θ是水平轴（x轴）逆时针旋转，与碰到的矩形的第一条边的夹角。并且这个边的边长是width，另一条边边长是height。也就是说，在这里，width与height不是按照长短来定义的。
在opencv中，坐标系原点在左上角，相对于x轴，逆时针旋转角度为负，顺时针旋转角度为正。

完整演示代码

为了直观起见, 我们可以直接这样赋值：👇

((cx, cy), (width, height), theta) = cv2.minAreaRect(cnt)

演示样例循环:👇

for cidx,cnt in enumerate(contours):
    ((cx, cy), (width, height), theta) = cv2.minAreaRect(cnt)
    print('center: cx=%.3f, cy=%.3f, width=%.3f, height=%.3f, roate_angle=%.3f'%(cx, cy, width, height, theta))

完整代码如下：👇

import numpy as np
import cv2

# 读入黑背景下的彩色手写数字
img = cv2.imread("color_number_handwriting.png")
# 转换为gray灰度图
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 寻找轮廓
contours, hier = cv2.findContours(gray, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

# 声明画布 拷贝自img
canvas = np.copy(img)

for cidx,cnt in enumerate(contours):
    minAreaRect = cv2.minAreaRect(cnt)
    # 转换为整数点集坐标
    rectCnt = np.int64(cv2.boxPoints(minAreaRect))
    # 绘制多边形
    cv2.polylines(img=canvas, pts=[rectCnt], isClosed=True, color=(0,0,255), thickness=3)

cv2.imwrite("number_minarearect_canvas.png", canvas)

运行效果

运行代码，在后台显示结果如下：

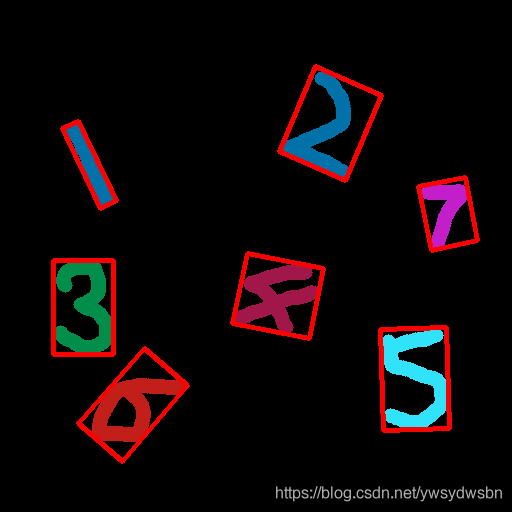
输出结果：

center: cx=133.105, cy=404.773, width=100.107, height=57.519, roate_angle=-49.185 
center: cx=415.190, cy=378.853, width=66.508, height=100.537, roate_angle=-1.710  
center: cx=278.323, cy=296.089, width=71.608, height=78.065, roate_angle=-78.440  
center: cx=83.000, cy=307.000, width=60.000, height=94.000, roate_angle=0.000     
center: cx=448.346, cy=213.731, width=47.068, height=64.718, roate_angle=-11.310  
center: cx=89.642, cy=164.695, width=17.204, height=88.566, roate_angle=-25.427   
center: cx=330.578, cy=123.387, width=92.325, height=72.089, roate_angle=-66.666

提取最小外接矩形区域

我们可以根据minAreaRect
函数返回的数据结构，以矩形中心(cx, cy)
作为对原来图像旋转的中心点，旋转角度设定为theta ：minAreaRect
函数用于获取最小面积的矩形:👇

# 声明旋转矩阵
rotateMatrix = cv2.getRotationMatrix2D((cx, cy), theta, 1.0)
# 获取旋转后的图像
rotatedImg = cv2.warpAffine(img, rotateMatrix, (img.shape[1], img.shape[0]))

具体代码如下：👇

'''
    利用minAreaRect绘制最小面积矩形并绘制
'''
import numpy as np
import cv2

# 读入黑背景下的彩色手写数字
img = cv2.imread("color_number_handwriting.png")
# 转换为gray灰度图
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 寻找轮廓
contours, hier = cv2.findContours(gray, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

for cidx,cnt in enumerate(contours):
    minAreaRect = cv2.minAreaRect(cnt)
    # 转换为整数点集坐标
    # rectCnt = np.int64(cv2.boxPoints(minAreaRect))
    ((cx, cy), (w, h), theta) = minAreaRect

    cx = int(cx)
    cy = int(cy)
    w = int(w)
    h = int(h)
    # 获取旋转矩阵
    rotateMatrix = cv2.getRotationMatrix2D((cx, cy), theta, 1.0)
    rotatedImg = cv2.warpAffine(img, rotateMatrix, (img.shape[1], img.shape[0]))
    pt1 = (int(cx - w/2), int(cy - h/2))
    pt2 = (int(cx + w/2), int(cy + h/2))
    # 原图绘制矩形区域
    cv2.rectangle(rotatedImg, pt1=pt1, pt2=pt2,color=(255, 255, 255), thickness=3)
    # 绘制中心点
    cv2.circle(rotatedImg, (cx, cy), 5, color=(255, 0, 0), thickness=-1)
    cv2.imwrite("minarearect_cidx_{}.png".format(cidx), rotatedImg)

运行效果如下：👇

数字样本图像转换为统一尺寸

我们截取了包含数字的外接矩形，他们形状各异。(可能需要手动旋转)👇

如果是制作神经网络所需要的样本图片的话，我们就需要将其放缩到统一大小。

接下来我们将图片统一变换到15*25
并转换为二值化图像。👇

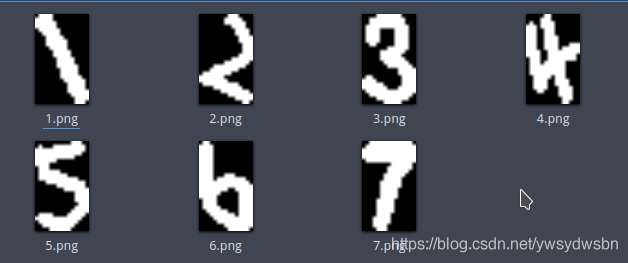
具体代码如下：👇

import numpy as np
import cv2
from glob import glob

img_paths = glob('./数字图像处理/*.png')

# 新的维度为10×20
new_dimension = (15, 25)

for img_path in img_paths:
    # 读入灰度图
    img = cv2.imread(img_path,cv2.IMREAD_GRAYSCALE)
    img_name = img_path.split('/')[-1]
    # 缩放
    resized = cv2.resize(img, new_dimension)
    # 二值化图片
    ret,thresh = cv2.threshold(resized,10,255,0)

    cv2.imwrite('./number/'+img_name,thresh)

「❤️ 感谢大家」

如果你觉得这篇内容对你挺有有帮助的话：

点赞支持下吧，让更多的人也能看到这篇内容（收藏不点赞，都是耍流氓 -_-）
欢迎在留言区与我分享你的想法，也欢迎你在留言区记录你的思考过程。
觉得不错的话，也可以阅读近期梳理的文章（感谢各位的鼓励与支持🌹🌹🌹）：

python开发之HighGUI上位机开发（一）(100+👍)
python开发之HighGUI上位机开发（二）：键盘事件监听、窗口销毁、窗口显示图像、滑动条组件、按键组件以及鼠标事件监听(120+👍)
python开发之HighGUI上位机开发（三）——项目实战：可变色画布和自制绘图板(120+👍)
基于混沌Logistic加密算法的图片加密与还原(160+👍)
一文带你彻底掌握数字化图像数据(210+👍)
先收藏！29个学术网站，比赛论文不再困难(230+👍)
【2020秋招面试】ML/DL/NLP/算法基础面试必看300问及答案（文末有下载方法）(220+👍)
Python 简单操作 Excel(230+👍)
Python 简单操作 Word (230+👍)
Python 简单操作 CSV (230+👍)
python之仿射变换分析：图像旋转及数学原理推导（210+👍）
python之图像仿射变换分析：原理+图像平移（220+👍）
python之图像仿射变换分析：图像翻转（110+👍）
python之图像仿射变换分析：图像旋转+图像缩放（120+👍）

「❤️ 资源传送门」

1. 扫码关注【做一个柔情的程序猿】公众号

2. 在【做一个柔情的程序猿】后台回复【python资料】【2020秋招】获取相应资料

👆长按上方二维码 2 秒
回复「python资料」即可获取python学习资料
回复「2020秋招」即可获取2020秋招面试题及答案

python

文章转载自做一个柔情的程序猿，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。