



1、问题定义
· Personalized PageRank:从源点s出发进行随机游走,每一步有α概率停止,有(1-α)/d_𝑜𝑢𝑡的概率沿任何一个出边继续走,又叫做PageRank with Restart。从s出发的随机游走,停在t点的概率就是s到t的PPR值,记做π(s,t).
· Single-source PPR query(单源PPR查询):固定源点s,对于图中所有点v得到ppr向量π(s,v),其中
· Single-target PPR query(单宿PPR查询):固定终止点t,对于图中所有点u有ppr向量π(u,t)
2.整体思路
对于每次增删边的动态图G,利用forward-push和backward-push技术(分别用来计算单源ppr和单宿ppr查询),通过更新残差r的值,再进行push,从而避免进行重新计算整个图的ppr。


伪码如下图所示:

初始情况下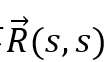 为1,从点v向外push的过程中,当前点的P(s,v)增加R(s,v)*α,将剩余的R(s,v)*(1-α)等分给出边的点,并把R(s,v)置0。选择
为1,从点v向外push的过程中,当前点的P(s,v)增加R(s,v)*α,将剩余的R(s,v)*(1-α)等分给出边的点,并把R(s,v)置0。选择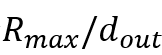 的好处是可以bound住push的时间复杂度为O(1/ε)。即对每个点v向外push的过程中总的残差R会减少至少
的好处是可以bound住push的时间复杂度为O(1/ε)。即对每个点v向外push的过程中总的残差R会减少至少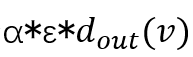 ,而对v点进行push的这一过程需要
,而对v点进行push的这一过程需要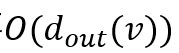 的时间。
的时间。
(2)Backward Push

类似地有伪码如下所示:

优势在于进行push之后可以直接用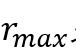 来bound任意点对的ppr误差,注意到push的过程是与forward-push不同的,R在分配出去的时候除以的是v点的出度,因为模拟的是每个点到达t的概率。
来bound任意点对的ppr误差,注意到push的过程是与forward-push不同的,R在分配出去的时候除以的是v点的出度,因为模拟的是每个点到达t的概率。
(3)Update Backward push
这部分是将原先的算法拓展到动态图上进行研究:

再写成局部性质,取向量的某一维得到下式

因此可以得到整体的伪代码:

(4)Update Forward Push
完全类似地,可以将Forward push算法进行推广

伪代码如下所示:

4.实验结果
主要与KDD15中的Tracking PPR算法进行了比较,在相近的精确度下用时有着较明显的缩短。


5.小结
· 算法本身的思路比较好理解,就是维护估计值(P)和残差(R),再通过push操作进行更新。
· 算法的复杂度限定大多是在无向图上完成,在有向图上没有那么好的性质,同时每次限定了只有一条边的增删,且不会出现新的点。且在forward-push中,无法做到对误差的较好估计。



1.问题定义
针对动态图上的单源PPR进行计算
2.整体思路
在第一篇论文的基础上,将push操作与Power-method算法相结合,利用矩阵运算优化,本质上是将forward-push的阈值设置为所有点的残差值之和,每一轮对所有残差点进行push。
3.算法介绍
(1)Cumulative Power Iteration
其中q为初始的偏好向量,即第s维为1的单位向量

本质上的矩阵运算与push一致:

对于图结构的更新,具体推导如下:

其中q为残差,r为最后的ppr估计值,A为原始的行归一化的邻接矩阵,B为增边之后行归一化的邻接矩阵,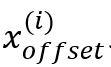 表示第i轮push的残差
表示第i轮push的残差
(2)OSP算法
算法的伪代码如下:

其中总的时间复杂度为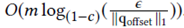 ,因为每一次矩阵运算,相当于把当前所有有残差的点push一次,剩余的残差减少到原来的(1-ε)
,因为每一次矩阵运算,相当于把当前所有有残差的点push一次,剩余的残差减少到原来的(1-ε)
4.实验结果
选取数据集,随机生成图流,分成两部分,前一半作为初始值,后一半分成了10个snapshot,每次给出一个snapshot来计算,与Lazy Forward Push,TrackingPPR进行了比较,用时和准确度都有一定的提升。

5.小结
利用矩阵运算来对于所有有残差值的点进行push操作,其优点在于,对于forward-push有了精确度保证,同时可以不需要像KDD16那样每次限定只能增删一条边就进行更新。



1.问题定义
针对动态图上SimRank的single-pair query问题进行解答
其中SimRank的内核为:如果两个点有相似的入邻边结构,那么这两个点也相似。递归定义如下:

基于随机游走的SimRank查询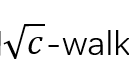 :给定图G中的一个顶点u,一个从u点出发的-
:给定图G中的一个顶点u,一个从u点出发的-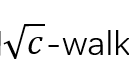 是满足以下条件的随机游走,即每一步有1-
是满足以下条件的随机游走,即每一步有1-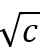 的概率停止,有的概率从当前节点的入边中等概率随机选择一条继续下去。那么u,v之间的SimRank值s(u,v) = Pr[w(u)和W(v)]相遇
的概率停止,有的概率从当前节点的入边中等概率随机选择一条继续下去。那么u,v之间的SimRank值s(u,v) = Pr[w(u)和W(v)]相遇
2.核心思路
将图G上的SimRank计算转化为笛卡尔积图G*G上的PPR计算,利用前后向随机游走相结合的方法进行研究。利用类似于KDD16的办法进行动态化更新。
文中定义了SimRank图和独立点(Singleton node)的概念



从而顺利将原图上两条随机游走的相遇问题转化为SimRank图上的PPR问题。并相应地提出了(1+c)-walk。其本质上就是在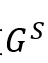 图上的随机游走,图实际上就是为了简化随机游走取样的过程,相当于直接从两个点同时出发,而且保证了相遇一定是第一次相遇
图上的随机游走,图实际上就是为了简化随机游走取样的过程,相当于直接从两个点同时出发,而且保证了相遇一定是第一次相遇

3.算法简介
(1)BLPMC算法=BLP+MC
BLP算法实际上就是前面提到的Forward-push算法的延伸,这一部分与介绍的第一和第二篇论文都有一定的相似性,

对于固定的一个点对(a,b)进行沿入边的push操作,开始时点对a,b的residue为1,之后每次push,总的residue(即为||h1||)都在减少,减少的量是在这一点停下的概率(第11行所示)。H表示残差向量。第6行本质上就是从a,b出发的随机游走在u’点相遇了,而s值增加的Δ就是从a,b出发的随机游走在这一点相遇的概率。
在BLP算法的基础上,作者与MC算法相结合,这一思路与FORA算法很相似,即从所有带有残差的点按照残差的大小来等比例引出随机游走。

(2)FLPMC=FLP(offline index) + MC(inline query)
类似地,FLP算法与之前提到的Backward-push算法很相似,伪码如下:

实际上是相当于从相遇点开始的反向随机游走,在途中经过的所有点对(即有相遇可能的点对)加上相应的残差数值.其中Offline 时间复杂度
类似地将FLP与MC相结合得到FLPMC算法:

这里的MC是从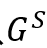 图中的(a,b)点开始随机游走,记录下来停止的点,再加上对应位置的residue。其中注意第7行的参数,因为随机游走模拟的是停在这个结点对的概率,而实际上应该为走到这个点且继续走下去的概率,所以为c/(1-c)
图中的(a,b)点开始随机游走,记录下来停止的点,再加上对应位置的residue。其中注意第7行的参数,因为随机游走模拟的是停在这个结点对的概率,而实际上应该为走到这个点且继续走下去的概率,所以为c/(1-c)
将FLP算法应用于动态图上,与第一篇论文十分相似,本质都是从局部更新残差,之后有选择地进行push操作。

其中对于残差更新的推导也很相近,(21)(22)分别表示了增删一条边(u,v)的情况, 每次增删一条边u,v需要对所有的点a进行下述更新,


(3)FBLPMC=FLP+BLP+MC
作者将上述三种算法都进行了结合,用于解决single-pair的查询

其中算法的空间复杂度为 ,
时间复杂度为
其中d为平均出度,S为BLP的push序列,nnz(R)指R矩阵中非零元数目
4.实验结果



可以看到在查询时间上:FBLPMC < FLPMC< BLPMC
在查询空间上:FBLPMC > FLPMC> BLPMC
动态更新代价:BLPMC < FLPMC =FBLPMC
精确度上也有比较不错的表现
5.小结
本文将SimRank计算转化为新图上的PPR计算,利用forward-push和backward-push和MC等多项技术的结合,并且动态地进行了index的更新。
这三篇论文本质上有一定的相似点,都是将Local-push(包括Forward-push和Backward-push)应用到动态图上,通过对残差进行更新,来实现快速计算新图上的相似度,取得了较好的效果。对于后续动态图上相似度的研究以及其他方向可能的应用有着较强的参考意义和启发价值。

 相 关 链 接
相 关 链 接







