局部回归,顾名思义就是在局部拟合回归模型。那也就是说,我们平时用到的回归分析,应该是全局回归(Global regression)。
古人云:“不谋全局者,不足以谋一域”。当我们考虑局部回归的时候,这说明局部发生了一些和全局不一样的事情。例如,全局可能是个线性模型,但是在局部出现了非线性。或者总的来说股市是上涨的,但是总有个别几天股市下跌。再或者,总的来说疫情是好转了,但是不排除在某一个时间,某一个地方疫情出现反弹。这些都说明局部可能和全局的情况不同,那么我们应该怎么刻画局部呢?
其实,我们之前介绍的多项式回归,基函数以及光滑样条都是可以用来解决局部和全局不同的问题。但是,办法总比问题多,我们来简单介绍一下局部回归。
局部回归是另一种拟合灵活非线性模型的方法。简答地说,局部回归利用目标点x_0附近的数据,拟合曲线。
当X=x_0时,局部回归的算法为:
1. 定义跨度s=k/n,获取x_0附近的点x_i;
2. 给这个区域内每个点分配权重K_i0=K(x_i,x_0)。越靠近x_0,权重越高。越远离x_0,权重越低。最远的点权重为0。
3. 利用加权x_i的数据,使用加权最小二乘法拟合y_i。寻找能使得
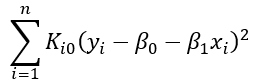
(1)
最小的beta_hat_0和beta_hat_1使得
4. 通过下式拟合x_0:

需要指出,对于不同的目标点x_0,权重K_i0也不同。那就是说,如果要估算一个新的目标点,就需要重新利用(1)式,拟合回归模型。所以,局部回归是一个基于记忆(memory-based)的过程。
为了使用局部回归,我们需要做一些准备。例如,如何定义权重函数K,在第3步里是否要拟合线性、多项式回归。
但是最重要的是如何选择第1步中定义的跨度s。它的作用和我们之前讲到的光滑样条中的参数lambda类似,都可以用来控制非线性拟合中的灵活性。跨度越小,那么局部回归的次数就更多,拟合出来的曲线就越弯曲。相反,如果跨度越大,那么局部回归的次数就越少,拟合出来的曲线就越平滑。在极端情况下,当跨度足够大,那么局部回归就会使用到全部训练数据拟合曲线。这就又回到了全局回归。
图1中展示了两个不同的局部回归,它们的跨度s分别为0.2和0.5。从图中可以看出,当s=0.5时,拟合出来的曲线更加光滑。
图1

那么如何选择s呢?我们可以根据经验自己设定,也可以使用交叉验证的办法选择s。而且,在实际工作中,我们经常会使用不均匀的跨度。
具体有关跨度选择,对称误差以及多元局部回归的问题比较复杂。有兴趣的朋友可以留言探讨。






