
LeetCode 200题,链接:https://leetcode-cn.com/problems/number-of-islands
除了解决该题目,阅读本文,可以 get 到以下点:
染色法 并查集的灵活应用
一、题目要求
给定一个由 '1'(陆地)和 '0'(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
大白话就是:计算二维网格中有几堆 1,上下或者左右相邻的 1 被认为是同一堆。如下图所示,左图中有 3 堆1,右图中 1 全是相邻的,所以认为是一堆 1。

解题思路主要是两种:染色法和并查集。下面分别讲述两种方法的思路和代码实现。不了解并查集的同学可以参考我的上一篇文章:《一文搞懂并查集》 。
二、染色法
解题思路
遍历过程中,将遍历完的 1 进行染色,染色就是将 1 改为 2,或者改为 0。不同数值表示不同的颜色。遍历过程中,一旦发现元素 1,意味着肯定发现了一个岛,那么岛数量 +1,同时把当前元素递归染色,将所有递归到的元素 1 全部改成 2。改为 2 表示当前岛已经遍历过了,以后再遍历到该岛时岛的数量不应该 +1。注意,这里一定是递归染色,而不是仅仅把相邻的元素 1 改成 2。
如下图所示,是染色的正确姿势,遍历到左上角第一个元素 1 时,意味着肯定发现了一个岛。此时将岛的数量 +1,并将该岛的所有元素 1 都染色变成 2,表示当前岛已经遍历完成,下次遇到该岛上的元素时,岛数量不能 +1。
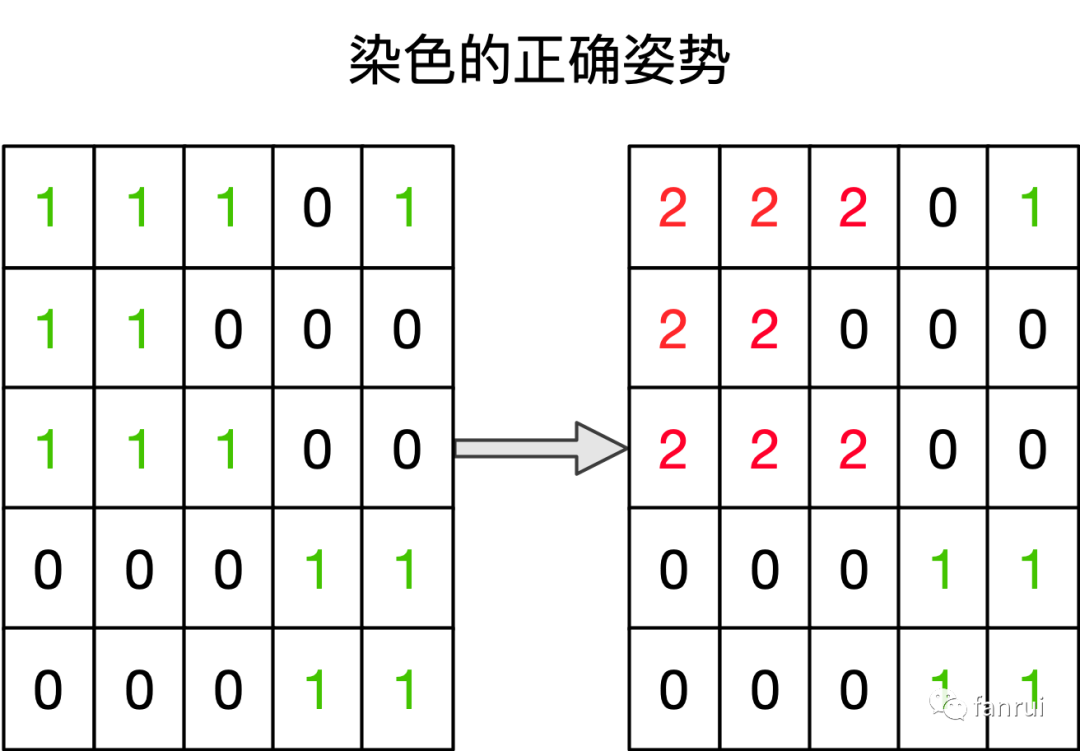
如下图所示,是染色的错误示范,遍历到左上角第一个元素 1 时,岛数量 +1,只将自己以及上下左右相邻的元素染色。当遍历到第一行第三个元素 1 时,又将岛数量 +1,但是这都属于同一个岛,并不应该 +1。看到这里相信读者已经清晰地明白染色规则了。
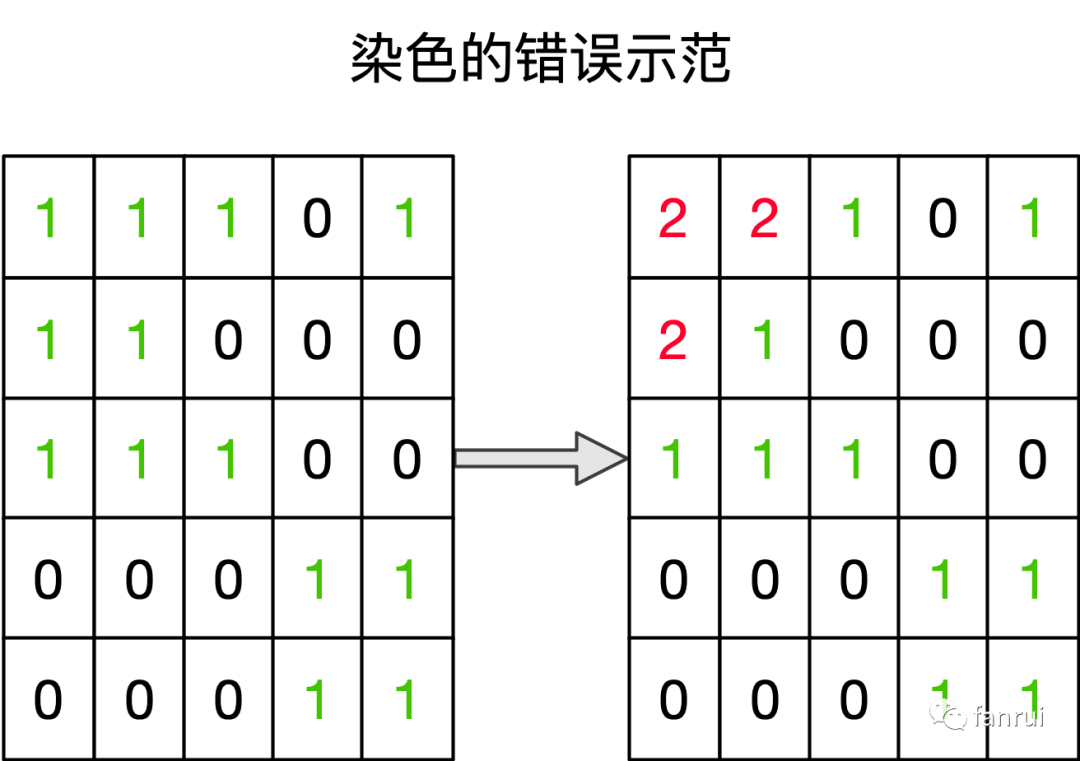
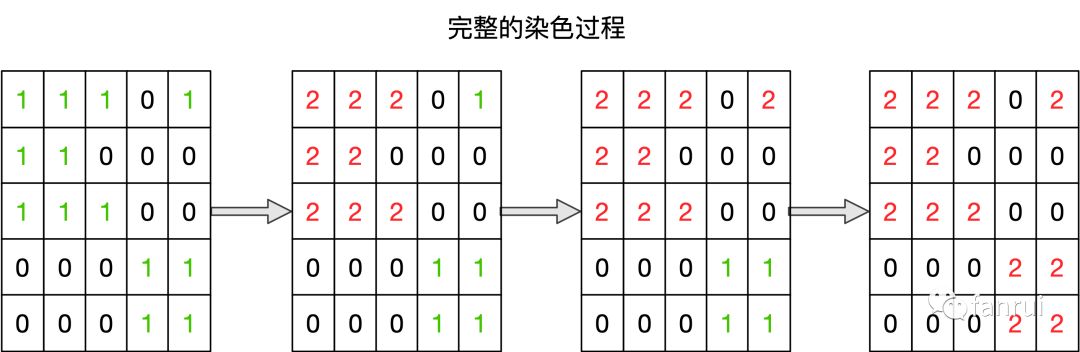
完整的染色过程如下图所示,总共染色三波,每一波岛数量 +1,所以岛的数量为 3。统计结束!!!
代码实现
染色的过程就是挨个遍历所有元素的过程。按照二维数组,一行一行依次遍历,当发现元素值为 1 时,岛数量 +1,并将当前岛上所有元素染色成 2。当前岛上所有元素已经变成了 2,因此后续的遍历过程中,该岛肯定不会重复计算。遍历代码如下所示,拿到二维数组的行数和列数,两层 for 循环依次遍历所有元素,如果元素为 1,则岛数量 +1,并执行染色操作:
public static int numIslands(char[][] grid) {
if (grid == null || grid.length == 0 ) {
return 0;
}
// 二维数组的行数
int R = grid.length;
// 二维数组的列数
int C = grid[0].length;
int res = 0;
// 遍历所有元素
for (int r = 0; r < R; r++) {
for (int c = 0; c < C; c++) {
// 发现元素是 1
if (grid[r][c] == 1) {
// 岛数量 +1
res++;
// 染色
infect(grid, r, c, R, C);
}
}
}
return res;
}
染色函数要实现什么样的功能呢?就是传进来一个坐标,要把这个坐标所在岛的元素全部染色。代码如下所示,首先使用 m[i][j] = 2;
将自己染色成 2,然后递归上下左右四个方向即可。递归肯定有终止条件,如果当前元素是数组第一列元素,再往左递归,必然会数组越界。同理第一行元素往上递归也会数组越界。最后一列、最后一行也是同理。因此出现 i < 0 || i >= N || j < 0 || j >= M
时直接 return 即可,不染色。还有一个限制条件,只有元素为 1,才进行染色,所以递归过程中,出现了 m[i][j] != 1
也要 return,结束递归。
// 四个方向都需要染色
private static void infect(char[][] m, int i, int j, int N, int M) {
if (i < 0 || i >= N || j < 0 || j >= M || m[i][j] != 1) {
return;
}
// 将自己所在节点染色
m[i][j] = 2;
// 递归遍历上下左右四个方向进行染色
infect(m, i + 1, j, N, M);
infect(m, i - 1, j, N, M);
infect(m, i, j + 1, N, M);
infect(m, i, j - 1, N, M);
}
算法思想和算法都比较容易实现,完整代码如下所示,笔者使用的整数 1,LeetCode 200题使用的是字符 1,即 '1',这些细节也需要注意:
public static int numIslands(char[][] grid) {
if (grid == null || grid.length == 0 ) {
return 0;
}
// 二维数组的行数
int R = grid.length;
// 二维数组的列数
int C = grid[0].length;
int res = 0;
// 遍历所有元素
for (int r = 0; r < R; r++) {
for (int c = 0; c < C; c++) {
// 发现元素是 1
if (grid[r][c] == 1) {
// 岛数量 +1
res++;
// 染色
infect(grid, r, c, R, C);
}
}
}
return res;
}
// 四个方向都需要染色
private static void infect(char[][] m, int i, int j, int N, int M) {
if (i < 0 || i >= N || j < 0 || j >= M || m[i][j] != 1) {
return;
}
// 将自己所在节点染色
m[i][j] = 2;
// 递归遍历上下左右四个方向进行染色
infect(m, i + 1, j, N, M);
infect(m, i - 1, j, N, M);
infect(m, i, j + 1, N, M);
infect(m, i, j - 1, N, M);
}
上述染色过程使用的是深度遍历,当然也可以使用广度遍历来实现染色。广度遍历类似于树的按层次遍历,都需要借助队列来实现,有兴趣的同学可以自己实现。感觉有难度的同学可以参考 LeetCode 200 题的题解区域。
三、并查集
并查集(union & find)是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。对并查集不了解的同学再次推荐一下我写的上一篇文章 《一文搞懂并查集》,如果不了解并查集下面的讲述肯定看不懂的。
解题思路
使用并查集解决这道题,主要思路是:初始状态时将每一个值为 1 的元素看做一个单独的集合,然后将将上下左右相邻的集合进行合并,最后剩余几个集合就是几个岛。换言之,可以将一个岛理解为一个帮派,每个岛上只有一个老大(代表节点),其余的都是小弟。初始化时,所有的元素都是单独的集合,且是集合的老大。遍历过程中,将上下左右相邻的帮派进行合并。合并之后,每个岛只有一个老大,集合的数量就是岛的数量。
遍历完之后,如何获取集合的数量呢?并不好获取,除非把所有元素遍历一遍,parent 指向自己的元素就是老大,老大的数量就是岛的数量。这样做可以,但是效率可能较低,合并结束后还需要将所有元素遍历一遍。于是,想了一个更好的方案来计算岛的数量。初始化时,认为每个元素是一个岛,所以初始化后,岛的数量就是数组中元素 1 的个数。当两个集合进行合并操作时,就是将两个集合合并为一个集合,所以集合数量 -1。到最后遍历完就可以直接获取到集合的个数。
上述就是并查集求解岛问题的思路,下面开始分析代码实现。
代码实现
首先要构建一个并查集,构建的并查集 UnionFind 与普通并查集没有什么区别,主要是一个 parent 数组和一个 rank 数组。增加了一个 count 字段,用来表示岛的数量,最后可以直接返回统计结果。初始化后,count 为元素 1 的个数。每次 union 操作,将 count 值 -1。
在该题目中,并查集构建的过程可能有点区别,区别主要在于输入的是一个二维数组,而我们的并查集中 parent 和 rank 都是一维数组。如何解决这个问题呢?直接将二维数组拍平,就可以放到一维数组中。说白了,把二维数组第二行跟在了第一行的后面,第三行跟在第二行后面,依次类推,将二维数组拍平。具体如何实现呢?
使用 r*C + c
将二维数组映射到一维数组,C 表示二维数组的列数,r 表示当前处于第几行,c 表示当前处于第几列。假设输入的 grid 是一个 4 行 5 列的二维数组,那么 index = r*C + c= r*5+c
是这么存储的:
第 0 行,r = 0, index = 0*5+c = c
第 1 行,r = 1, index = 1*5+c = 5+c
第 2 行,r = 2, index = 2*5+c = 10+c
第 3 行,r = 3, index = 3*5+c = 15+c
并查集的 find 和 union 方法,与上一篇文章普通并查集的方法一模一样,没有任何修改。并查集代码如下所示,可以结合注释过一遍。
class UnionFind{
// count 表示岛的数量
int count;
/**
* 使用一个数组 parent,第 i 位上的元素存储着 j,表示 i 的 parent 是 j
* 初始化时,每一位都存储自己的下标,即:第 i 位上的元素存储着 i,第 j 位上的元素存储着 j,
* 来表示每一位都指向自己。
*/
int[] parent;
/**
* rank 数组用来保存集合的高度,第 i 位上元素存储着 j,
* 表示以 i 为代表节点的集合高度为 j
*/
int[] rank;
/**
* 将二维数组 grid 初始化成 并查集。
* parent 是一维数组,怎么保存二维数组 grid 中的数据呢?
* 说白了,把二维数组第二行跟在了第一行的后面,第三行跟在第二行后面,依次类推,将二维数组拍平
* 使用 r*C + c 将二维数组映射到一维数组,
* C 表示二维数组的列数,r 表示当前处于第几行,c 表示当前处于第几列
* 假设 grid 是一个 4 行 5 列的二维数组,那么 index = r*C + c= r*5+c 是这么存储的:
* 第 0 行,r = 0, index = 0*5+c = c
* 第 1 行,r = 1, index = 1*5+c = 5+c
* 第 2 行,r = 2, index = 2*5+c = 10+c
* 第 3 行,r = 3, index = 3*5+c = 15+c
* @param grid
*/
UnionFind(char[][] grid) {
int R = grid.length;
int C = grid[0].length;
parent = new int[C*R];
rank = new int[C*R];
int res = 0;
// 遍历所有元素
for (int r = 0; r < R; r++) {
for (int c = 0; c < C; c++) {
// 初始化 parent、rank 数组, count 存储 1 的个数
if (grid[r][c] == 1) {
parent[r*C + c] = r*C + c;
rank[r*C + c] = 0;
// 初始化后,count 为元素 1 的个数
count ++;
}
}
}
}
// 递归查找代表节点,顺便压缩路径
public int findHead(int i){
if(i != parent[i]){
parent[i] = findHead(parent[i]);
}
return parent[i];
}
/**
* 合并集合 i 、j
* @param i
* @param j
*/
public void union(int i, int j) {
int iHead = findHead(i);
int jHead = findHead(j);
// 两个元素是一个集合,直接返回
if(iHead == jHead){
return;
}
// 元素数量少的集合 指向元素数量大的集合,并更新 rank
if(rank[iHead] < rank[jHead]){
parent[iHead] = jHead;
} else if (rank[iHead] > rank[jHead]){
parent[jHead] = iHead;
} else {
parent[iHead] = jHead;
rank[jHead] += 1;
}
// 每合并一次,岛的数量 -1
count--;
}
public int getCount() {
return count;
}
}
并查集设计好了,接下来就是主方法了,主方法的工作是:
构建并查集 count 为元素 1 的个数 遍历所有元素为 1 的元素,执行相应的合并操作 合并操作是将同一个岛上的集合合并,若合并成功,则 count 值减 1 最后直接返回 count 值即可
具体代码如下所示:
public int numIslands(char[][] grid) {
if(grid==null || grid.length == 0){
return 0;
}
UnionFind unionFind = new UnionFind(grid);
int R = grid.length;
int C = grid[0].length;
for (int r = 0; r < R; r++) {
for (int c = 0; c < C; c++) {
// 遍历所有值为 1 的元素
if (grid[r][c] == 1) {
// 左边如果为 1,与左节点 union
if(c > 0 && grid[r][c-1] == 1) {
unionFind.union(r*C + c -1,r*C + c);
}
// 上边如果为 1,与上节点 union
if(r > 0 && grid[r-1][c] == 1){
unionFind.union((r-1)*C + c,r*C + c);
}
}
}
}
return unionFind.getCount();
}
有没有发现一个细节,这里的合并操作,只与左边节点和上边节点做了合并,并没有与右边节点和下边节点合并。会不会导致同一个岛上一些元素没有被合并呢?举一个左右的例子,上下的场景类似:
A、B、C 位置上三个元素都是 1 要进行合并,A 在 B 的左边,B 在 C 左边。假如我们只合并左元素,会不会漏掉呢?首先遍历 A,A 左边没有元素,所以不合并;然后遍历 B,B 左边是 A 元素,所以 B 和 A 会合并成一个集合;最后遍历 C,C 左边是 B 元素,所以 C 和 B 会合并成一个集合;所以 A、B、C 可以保证合并到一个集合中。为什么可以,是因为 B 处于 C 左侧,B 不与 C 合并,C 必然要与 B 合并。所以不会漏掉。
染色法能不能只朝两个方向染色?
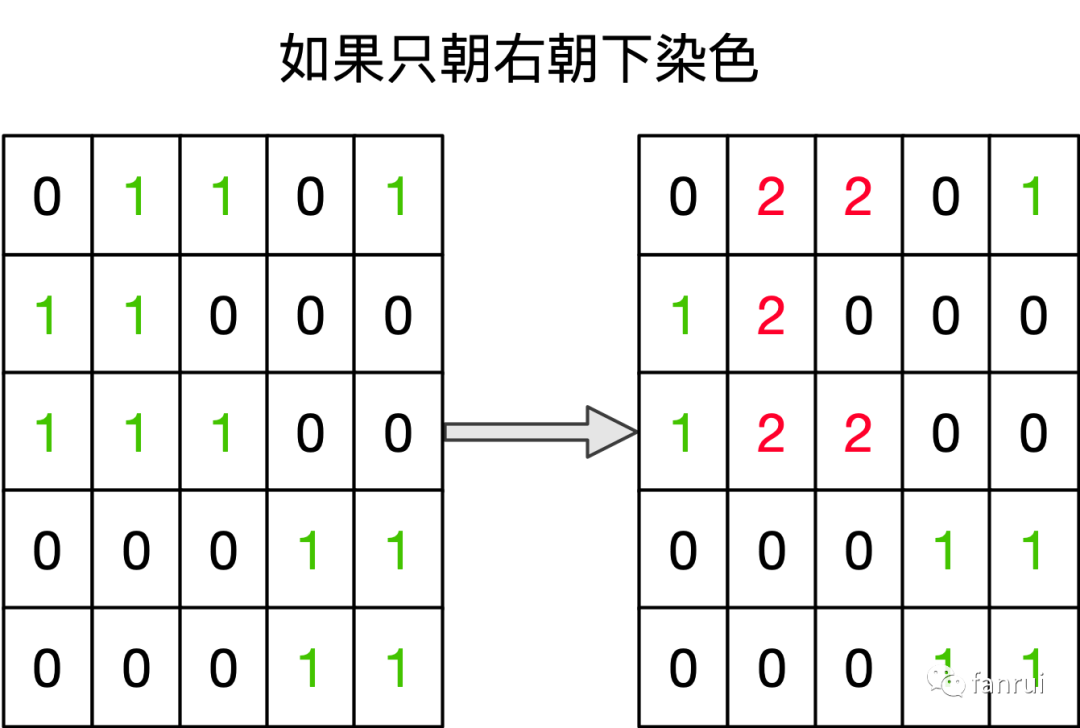
但是之前的染色法,我们就是朝四个方向去染色,那种场景,能不能改成两个方向去染色呢?答:不可以。染色法求岛的数量,依据的是只要碰到一个 1,就要该岛所有元素染色,保证每个岛只会计数一次,下次遍历到岛上其他节点不会再被计数。既然要把当前岛上所有元素找到,就不能只朝两个方向去找。下面给一个案例:
数组从左向右遍历,因此染色时朝右朝下递归染色。遍历过程中,第一次会碰到第 0 行第 1 列的元素 1,然后将岛数量 +1,开始染色,由于只朝两个方向染色,因此第一个岛上漏掉了两个元素没有染色成功。所以染色法必须朝四个方向去染色。
四、小结
详细分析了两种方法去求岛的个数,读者一定要把两种思路都掌握。相信大家把这篇文章和上一篇 《一文搞懂并查集》 搞懂,一定可以灵活解决并查集相关的算法问题。在解决并查集问题时,要学会灵活的将数据转换成并查集的结构,例如本文的二维数组转一维数组。遇到查找、合并集合,最后查集合数量的场景,一定要想到使用并查集来解决。当然染色法也是一种好思路,但遇到新的题目可能染色法不能解决,但是并查集可以解决。
本文的相关代码及并查集的相关代码请参考下面的链接:https://github.com/1996fanrui/fanrui-learning/tree/master/module-algo/src/main/java/com/dream/tree/unionfind







