python实现之导数

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'（x0）或df（x0）/dx。

不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。然而，可导的函数一定连续；不连续的函数一定不可导。

切线指的是一条刚好触碰到曲线上某一点的直线。更准确地说，当切线经过曲线上的某点（即切点）时，切线的方向与曲线上该点的方向是相同的。平面几何中，将和圆只有一个公共交点的直线叫做圆的切线。

法线（normal line），是指始终垂直于某平面的直线。在几何学中，法线指平面上垂直于曲线在某点的切线的一条线。法线也应用于光学的平面镜反射上。

#!/usr/bin/env python# -*- coding: UTF-8 -*-#                     _ooOoo_#                   o8888888o#                    88" . "88#                 ( | -  _  - | )#                     O\ = O#                 ____/`---'\____#                  .' \\| |// `.#                  \\|||:|||// \#                _|||||-:- |||||- \#                | | \\\ -  | |#              | \_| ''\---/'' | _/ |#               \ .-\__ `-` ___/-. #            ___`. .' --.--\ `. . __#         ."" '< `.___\_<|>_/___.' >'"".#       | | : `- \`.;`\  _ `;.`/ - ` : | |#          \ \ `-. \_ __\ __ _/ .-`  #      ==`-.____`-.___\_____/___.-`____.-'==#                     `=---=''''@Project ：pythonalgorithms @File ：derivatives.py@Author ：不胜人生一场醉@Date ：2021/8/1 0:17 '''import matplotlib.pyplot as pltimport numpy as npimport mathimport sympyimport mpl_toolkits.axisartist as axisartist  # 导入坐标轴加工模块if __name__ == '__main__':    quadraticderivativeplot()    exponentialderivativeplot()    arccscderivativeplot()

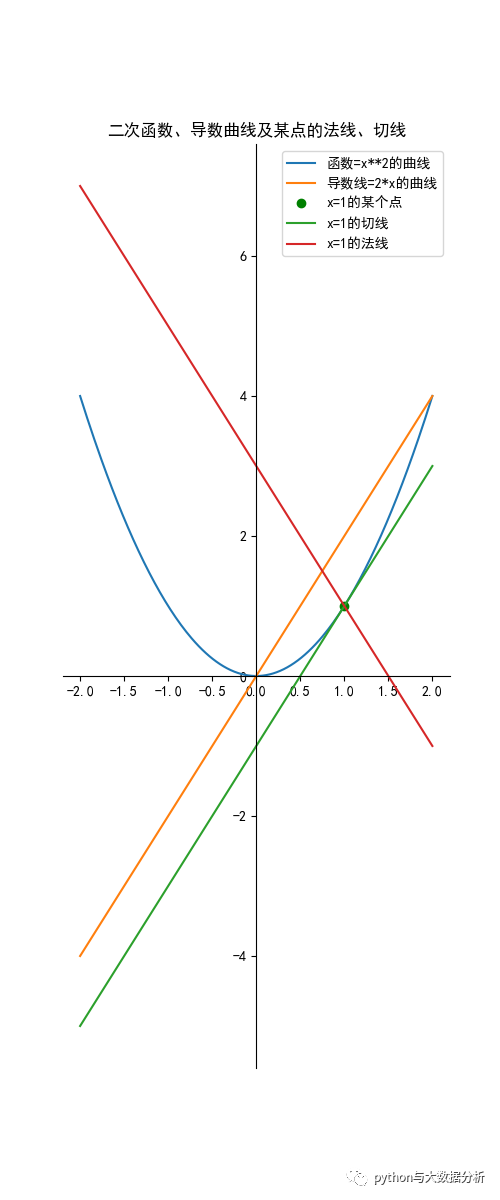
# 导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。# 当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'（x0）或df（x0）/dx。# 不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。# 若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。然而，可导的函数一定连续；不连续的函数一定不可导。def quadraticderivativeplot():    plt.figure(figsize=(5, 12))    ax = plt.gca()  # 通过gca:get current axis得到当前轴    plt.rcParams['font.sans-serif'] = ['SimHei']  # 绘图中文    plt.rcParams['axes.unicode_minus'] = False  # 绘图负号    x = np.linspace(-2, 2, 200)    y = x ** 2    label = '函数=x**2的曲线'    plt.plot(x, y, label=label)    yd = 2 * x    label = '导数线=2*x的曲线'    plt.plot(x, yd, label=label)    a = 1    ad = a ** 2    plt.plot(a, ad, 'og', label='x=1的某个点')    # y=ax+b,已知a=2,x=1,y=1，求b    b = ad - 2 * a    # 准备画切线的数据    al = np.linspace(-2, 2, 200)    yl = 2 * al + b    label = 'x=1的切线'    plt.plot(al, yl, label=label)    # 准备画法线的数据，切线斜率=法线斜率的负数    b = ad + 2 * a    al = np.linspace(-2, 2, 200)    yl = -2 * al + b    label = 'x=1的法线'    plt.plot(al, yl, label=label)    # 求导函数    x = sympy.Symbol('x')    f1 = x ** 2    # 参数是函数与变量    f1_ = sympy.diff(f1, x)    print(f1_)    # 设置图片的右边框和上边框为不显示    ax.spines['right'].set_color('none')    ax.spines['top'].set_color('none')    # 挪动x，y轴的位置，也就是图片下边框和左边框的位置    # data表示通过值来设置x轴的位置，将x轴绑定在y=0的位置    ax.spines['bottom'].set_position(('data', 0))    # axes表示以百分比的形式设置轴的位置，即将y轴绑定在x轴50%的位置    # ax.spines['left'].set_position(('axes', 0.5))    ax.spines['left'].set_position(('data', 0))    plt.title("二次函数、导数曲线及某点的法线、切线")    plt.legend(loc='upper right')    plt.show()

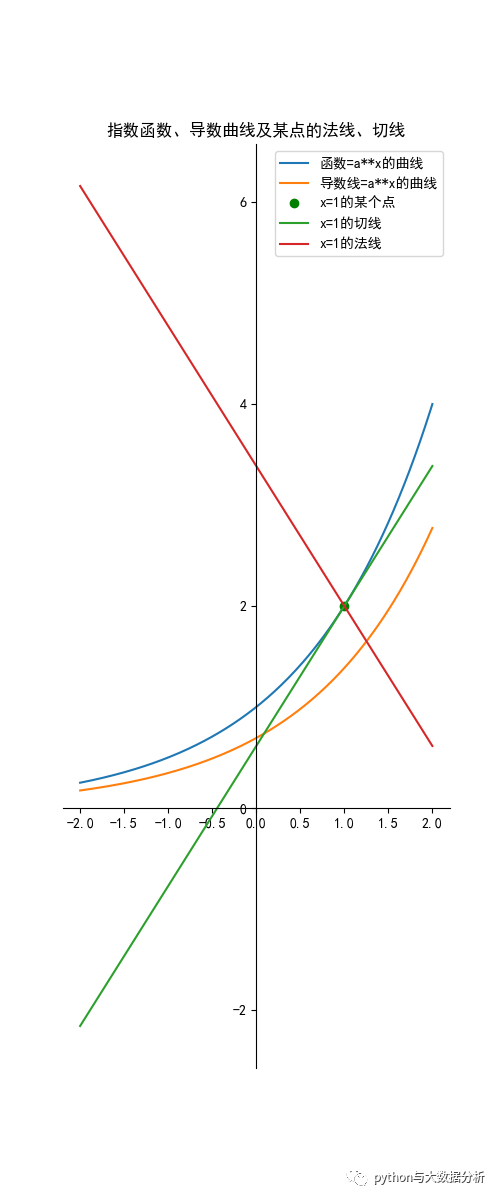
# 指数函数的导数# 指数函数 y=a**x# 指数函数的导数为 y=a**x*ln(a)def exponentialderivativeplot():    plt.figure(figsize=(5, 12))    ax = plt.gca()  # 通过gca:get current axis得到当前轴    plt.rcParams['font.sans-serif'] = ['SimHei']  # 绘图中文    plt.rcParams['axes.unicode_minus'] = False  # 绘图负号    a = 2    x = np.linspace(-2, 2, 200)    y = np.power(a, x)    yd = np.power(a, x) * np.log(a)    label = '函数=a**x的曲线'    plt.plot(x, y, label=label)    label = '导数线=a**x的曲线'    plt.plot(x, yd, label=label)    xpoint = 1    ypoint = np.power(a, xpoint)    plt.plot(xpoint, ypoint, 'og', label='x=1的某个点')    # 斜率slope=导数，求截距intercept    slope = math.pow(a, xpoint) * math.log(a, np.e)    # y=ax+b,已知a,x,y，求b    intercept = ypoint - slope * xpoint    # 准备画切线的数据    yl = x * slope + intercept    # print(slope,intercept,yl)    label = 'x=1的切线'    plt.plot(x, yl, label=label)    # 准备画法线的数据，切线斜率=法线斜率的负数    # y=ax+b,已知x,y,-a,求b    intercept = ypoint + slope * xpoint    yl = -x * slope + intercept    label = 'x=1的法线'    plt.plot(x, yl, label=label)    # # 求导函数    # x = sympy.Symbol('x')    # f1 = x**2    # # 参数是函数与变量    # f1_ = sympy.diff(f1, x)    # print(f1_)    # 设置图片的右边框和上边框为不显示    ax.spines['right'].set_color('none')    ax.spines['top'].set_color('none')    # 挪动x，y轴的位置，也就是图片下边框和左边框的位置    # data表示通过值来设置x轴的位置，将x轴绑定在y=0的位置    ax.spines['bottom'].set_position(('data', 0))    # axes表示以百分比的形式设置轴的位置，即将y轴绑定在x轴50%的位置    # ax.spines['left'].set_position(('axes', 0.5))    ax.spines['left'].set_position(('data', 0))    plt.title("指数函数、导数曲线及某点的法线、切线")    plt.legend(loc='upper right')    plt.show()

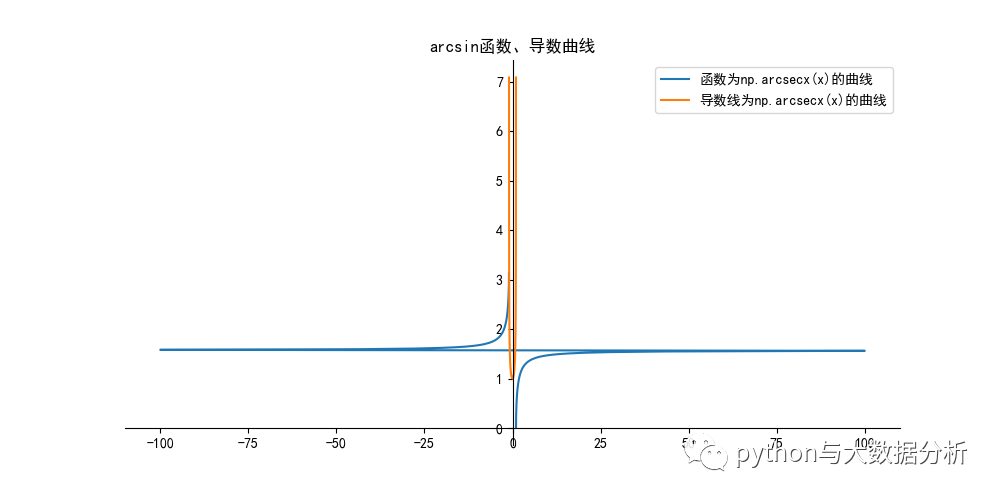
# 常用导数公式表如下：## c'=0(c为常数）# (x^a)'=ax^(a-1),a为常数且a≠0# (a^x)'=a^xlna# (e^x)'=e^x## (logax)'=1/(xlna),a>0且 a≠1# (lnx)'=1/x# (sinx)'=cosx# (cosx)'=-sinx# (tanx)'=(secx)^2# (secx)'=secxtanx# (cotx)'=-(cscx)^2# (cscx)'=-csxcotx# (arcsinx)'=1/√(1-x^2)# (arccosx)'=-1/√(1-x^2)# (arctanx)'=1/(1+x^2)# (arccotx)'=-1/(1+x^2)# arcsinx函数的导数# arcsinx函数# arcsinx函数的导数为 1/√(1-x^2)def arccscderivativeplot():    plt.figure(figsize=(10, 5))    ax = plt.gca()  # 通过gca:get current axis得到当前轴    plt.rcParams['font.sans-serif'] = ['SimHei']  # 绘图中文    plt.rcParams['axes.unicode_minus'] = False  # 绘图负号    x = np.append(np.linspace(0.01, np.pi  2 - 0.01, 120),                  np.linspace(np.pi  2 + 0.01, np.pi - 0.01, 120))    y = 1 / np.cos(x)    # 正割函数 sec(x)=1/cos(x)    # 反正割函数 颠倒x,y值即可    label = '函数为np.arcsecx(x)的曲线'    plt.plot(y, x, label=label)    x = np.linspace(-0.99, 0.99, 120)    yd = 1 / np.sqrt(1 - np.power(x, 2))    label = '导数线为np.arcsecx(x)的曲线'    plt.plot(x, yd, label=label)    # 设置图片的右边框和上边框为不显示    ax.spines['right'].set_color('none')    ax.spines['top'].set_color('none')
    # 挪动x，y轴的位置，也就是图片下边框和左边框的位置
    # data表示通过值来设置x轴的位置，将x轴绑定在y=0的位置
    ax.spines['bottom'].set_position(('data', 0))
    # axes表示以百分比的形式设置轴的位置，即将y轴绑定在x轴50%的位置
    # ax.spines['left'].set_position(('axes', 0.5))
    ax.spines['left'].set_position(('data', 0))
    plt.title("arcsin函数、导数曲线")
    plt.legend(loc='upper right')
    plt.show()