PostgreSQL 生成任意基数数独 - 1

作者

digoal

日期

2018-03-19

标签

PostgreSQL , 数独

背景

不知道什么时候开始数独游戏风靡起来了，数独游戏由一个N*N的矩阵组成，N必须是一个可以被开根的数值，例如4,9,16,25等。

任意一个像素，必须在三个方向上保证值唯一。这三个方向分别是X,Y,BOX。XY很好理解就是纵横的一条线（X,Y的像素个数就是N）。BOX指这个像素所在的BOX（BOX是由 (N的平方根)*(N的平方根) 个像素组成的矩阵）。

如图，一个9*9个像素的数独。（我把基数称为3）

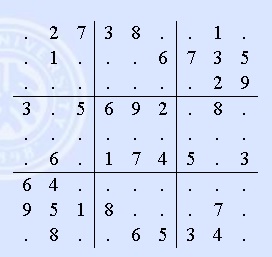
16*16的数独，16行，16列。同时分成4*4个BOX。（我把基数称为4）

那么如何生成一个有解的数独呢？

这个方法可行吗？

以下方法是按从左到右，从上到下的顺序来生成随机数的，看起来可行，实际上大多数情况下都无法生成有解数独，因为前面还比较容易满足条件，后面基本上就无法满足条件了。

```
create or replace function gen_sudoku(
dim int -- 基数
) returns int[] as $$
declare
res int[];
vloops int := 2 * (dim^5);
vloop int :=0;
ovloops int := 2 * (dim^5);
ovloop int :=0;
rand int;
begin
-- 初始化矩阵
select array( select (select array_agg(0) from generate_series(1,(dim^2)::int)) from generate_series(1,(dim^2)::int)) into res;

loop
-- 无法生成并返回
if ovloop >= ovloops then
raise notice '已循环%次，可能无法生成数独。', ovloop;
return res;
end if;
ovloop := ovloop+1;

<>
for x in 1..dim^2 loop
raise notice 'start again %', ovloop;
for y in 1..dim^2 loop
vloop := 0;
loop
-- 生成随机值
rand := 1+(random()*((dim^2)-1))::int;

    -- 这轮循环无法生成并返回  
if vloop >= vloops then  
  -- raise notice '1  %此数已循环%次，可能无法生成数独。', rand, vloop;  
  -- return res;  
  exit outer;  
end if;  
vloop := vloop+1;

    -- 横向验证  
    perform 1 where array(select res[x][generate_series(1,(dim^2)::int)]) && array[rand];  
if found then  
  --raise notice '2  %此数已循环%次，可能无法生成数独。%', rand, vloop, array(select res[x][generate_series(1,(dim^2)::int)]) ;  
  continue;  
end if;

-- 纵向验证  
    perform 1 where array(select res[generate_series(1,(dim^2)::int)][y]) && array[rand];  
if found then  
  --raise notice '3  %此数已循环%次，可能无法生成数独。%', rand, vloop, array(select res[generate_series(1,(dim^2)::int)][y]);  
  continue;  
end if;

-- BOX验证  
    perform 1 where array(select res[xx][yy] from (select generate_series(((((x-1)/dim)::int)*dim)+1, ((((x-1)/dim)::int)*dim)+dim) xx) t1, (select generate_series(((((y-1)/dim)::int)*dim)+1, ((((y-1)/dim)::int)*dim)+dim) yy) t2) && array[rand];  
if found then  
  --raise notice '4  %此数已循环%次，可能无法生成数独。%', rand, vloop, array(select res[xx][yy] from (select generate_series(((((x-1)/dim)::int)*dim)+1, ((((x-1)/dim)::int)*dim)+dim) xx) t1, (select generate_series(((((y-1)/dim)::int)*dim)+1, ((((y-1)/dim)::int)*dim)+dim) yy) t2);  
  continue;  
end if;

-- 通过验证  
res[x][y] := rand;  
raise notice 'res[%][%] %', x, y, rand;  
-- 跳出循环  
exit;  
  end loop;  
end loop;

end loop;
end loop;
return res;
end;
$$ language plpgsql strict;
```

以上方法最大的问题是，因为是左右，前后顺序在生成数独，实际上越到后面，会导致可以填充的满足XYB约束值越少，甚至没有。

为了尽可能的每次填充的值都有较大概率，可以在生成顺序上进行调整，不使用从左到右，从上到下的方法。

而是每一步都选择在XYB方向上还有最大概率（即最多没有填充的值）的像素。（我不清楚下围棋先占4个角，是不是也是同样的道理？）

如何找到每个像素在XYB维度上还有多少个未填充的值？

输入一个矩阵，得到另一个矩阵，表示当前位置在XYB轴的未填充值的个数。（非空值的xyb返回x,y,0,0,0）因为非空值不需要再填充它，所以无所谓。

1、首先要创建一个类型，包括数独矩阵的 X,Y坐标。以及这个坐标的横、竖、BOX三个方向上的剩余未填充值的个数。

create type xyb as ( ax int, -- 横坐标 ay int, -- 纵坐标 x int, -- 横向还有多少未填充像素 y int, -- 竖向还有多少未填充像素 b int -- BOX内还有多少未填充像素 );

2、编写一个函数，用来计算一个为完成数独矩阵，其每一个像素的XYB值。

```
create or replace function comp_xyb(
int[], -- 包含一些值的数独二维矩阵，当像素值为0时，表示这个值没有填充
int -- 数独的基数（比如2,3，。。。），3就是常见的99数独，4就是1616数独。
)
returns xyb[] -- 返回一个复合类型的数组矩阵，矩阵像素和输入矩阵一样，每个像素表示这个像素在XYB轴上还有多少个没有填充的值（没有填充的值用0表示）
as $$
declare
dims int := ($2)^2; -- 基数的平方，表示行、列、BOX的像素个数。也是每个方向上的矩阵标记上限
res xyb[]; -- 结果

vx int; -- 横向还有多少未填充像素
vy int; -- 竖向还有多少未填充像素
vb int; -- BOX内还有多少未填充像素

lx int; -- box的X方向矩阵下标
ux int; -- box的X方向矩阵上标
ly int; -- box的Y方向矩阵下标
uy int; -- box的Y方向矩阵上标
begin
-- 初始化矩阵
select array (
select array( select format('(%s,%s,0,0,0)', x, y) from generate_series(1,dims) t(y))
from (select generate_series(1, dims) x) t
)
into res;

-- X坐标
for x in 1..dims loop
-- Y坐标
for y in 1..dims loop

  -- 如果这个像素的值不等于0，说明已经是一个已经填充过的像素，返回0,0,0  
  if ($1)[x][y] <> 0 then  
    -- 不计算已填充了非0值的像素  
continue;  
  else  
    -- x，计算X方向有多少个未填充的像素  
select sum(case arr when 0 then 1 else 0 end) from   
  (select ($1)[x][generate_series(1, dims)] as arr) t   
into vx;

-- y，计算Y方向有多少个未填充的像素  
select sum(case arr when 0 then 1 else 0 end) from   
  (select ($1)[generate_series(1, dims)][y] as arr) t   
into vy;

-- b，计算BOX内有多少个未填充的像素  
-- x下限  
  lx := ((x-1)/$2)::int * $2 + 1;  
-- x上限  
  ux := ((x-1)/$2)::int * $2 + $2;  
-- y下限  
  ly := ((y-1)/$2)::int * $2 + 1;  
-- y上限  
  uy := ((y-1)/$2)::int * $2 + $2;  
    -- 计算BOX内有多少个未填充的像素  
select sum(case arr when 0 then 1 else 0 end) from   
  (select ($1)[xx][yy] as arr from   
    (select generate_series(lx,ux) xx) t1, (select generate_series(ly,uy) yy) t2  
  ) t into vb;

-- 将XYB的值，写入结果变量的对应像素中  
res[x][y] := format('(%s,%s,%s,%s,%s)',x,y,vx,vy,vb)::xyb;  
  end if;  
end loop;

end loop;
return res;
end;
$$ language plpgsql strict immutable;
```

3、用法举例

计算以下2为基数，4*4的矩阵的xyb值

{1,2,3,4}, {0,1,1,0}, {0,1,1,0}, {0,1,1,0}

```
postgres=# select array(select (comp_xyb('{{1,2,3,4},{0,1,1,0},{0,1,1,0},{0,1,1,0}}', 2))[x][generate_series(1,4)]) from generate_series(1,4) t(x);
array

{"(1,1,0,0,0)","(1,2,0,0,0)","(1,3,0,0,0)","(1,4,0,0,0)"}
{"(2,1,2,3,1)","(2,2,0,0,0)","(2,3,0,0,0)","(2,4,2,3,1)"}
{"(3,1,2,3,2)","(3,2,0,0,0)","(3,3,0,0,0)","(3,4,2,3,2)"}
{"(4,1,2,3,2)","(4,2,0,0,0)","(4,3,0,0,0)","(4,4,2,3,2)"}
(4 rows)
```

使用unnest可以解开，按XYB三个方向总大小排序，再按某个方向最大排序，从而做到逐级收敛，真正每一次填充的像素，都是具备最大概率的像素。

```
postgres=# select * from unnest( comp_xyb('{{1,2,3,4},{0,1,1,0},{0,1,1,0},{0,1,1,0}}', 2) ) t where t.x+t.y+t.b <> 0 order by (t.x+t.y+t.b) desc, greatest(t.x,t.y,t.b) desc;

ax | ay | x | y | b ----+----+---+---+--- 3 | 1 | 2 | 3 | 2 3 | 4 | 2 | 3 | 2 4 | 1 | 2 | 3 | 2 4 | 4 | 2 | 3 | 2 2 | 1 | 2 | 3 | 1 2 | 4 | 2 | 3 | 1 (6 rows) ```

通过这个SQL得到了某个像素，这个像素的XYB方向上，还有最多的像素没有被填充。

因此这个像素如果生成一个随机值的话，违反数独的约束（或者叫冲突）的概率是最小的。

```
postgres=# select * from unnest( comp_xyb('{{1,2,3,4},{0,1,1,0},{0,1,1,0},{0,1,1,0}}', 2) ) t where t.x+t.y+t.b <> 0 order by (t.x+t.y+t.b) desc, greatest(t.x,t.y,t.b) desc limit 1;

ax | ay | x | y | b ----+----+---+---+--- 3 | 1 | 2 | 3 | 2 (1 row) ```

用AX,ZY坐标值，往矩阵的这个像素填充符合数独条件的随机值，可以大幅提高构造可解数独的概率。

小结

本文先介绍如何得到这样的一个像素，填充一个值进行，这个值的取值区间应该是最大的（最不会与数独的游戏规则违背），从而更大可能的生成一个完整可解的数独。

下面一篇文章再介绍如何生成一个N*N的数独。

参考

http://poj.org/problem?id=3074

NP完全问题近似求解。

《PostgreSQL 生成任意基数数独 - 1》

《PostgreSQL 生成任意基数数独 - 2》

《PostgreSQL 生成任意基数数独 - 3》

PostgreSQL 许愿链接

您的愿望将传达给PG kernel hacker、数据库厂商等, 帮助提高数据库产品质量和功能, 说不定下一个PG版本就有您提出的功能点. 针对非常好的提议，奖励限量版PG文化衫、纪念品、贴纸、PG热门书籍等，奖品丰富，快来许愿。开不开森.

9.9元购买3个月阿里云RDS PostgreSQL实例

PostgreSQL 解决方案集合

德哥 / digoal's github - 公益是一辈子的事.