大家都在用的多重填补，有哪些不为人知的小细节

朋友们好，又是周五啦。我们今天的推文填一下上周挖的坑，聊聊多重填补相关的内容。

其实，推文写到现在，NHANES只是内容的大边界，很多下面的子话题如权重，删除的影响，变量分组都是一些小的系列文章。之后我也会在保留NHNAES大标签的同时，把这些小的系列文章打上自己的标签，感兴趣的朋友点开标签就能找到相关的文章，应该也会方便一些。

那我们话不多说，先梳理一下本篇推送的内容架构：知识补充（缺失模式相关知识）→多重填补的步骤→多重填补需满足的假设→NHANES实际应用（简单版）→缺失比例对方法选择的影响。

01 基于缺失模式的缺失分类

我之前以为这种分类不重要，就没和大家提。但在多重填补中，缺失模式是一个非常重要的考量指标（具体模式和方法的对应关系我们之后做推送介绍）。

数据缺失按照缺失模式可以分为单调缺失模式、任意缺失模式。可参照下图加以理解。

↑

两种数据缺失模式图解

单调缺失模式：对数据集进行适当的行列变换后，矩阵呈层级缺失的模式。矩阵中的元素Yj缺失时，则对任意的p≥j，元素Yp也是缺失的。

任意缺失模式：数据缺失具有随意性，即使通过行列变换也无法看出任何规律。在实际研究中也更为常见。

02 多重填补的步骤

一般来说，多重填补会分为以下三步：

↑

多重填补步骤

1.为每个缺失值产生一套可能的填补值，这些值反映了无响应模型的不确定性；每一个值都被用来填补数据集中的缺失值，产生若干个完整数据集；

2.每一个填补数据集都用针对完整数据集的统计方法进行统计分析；

3.对来自于各个填补数据集的结果进行综合，产生最终的统计推断，这一推断考虑到了由于数据填补而产生的不确定性。

03 多重填补需满足的假设

在多篇参考资料中都有提到的一个假设是随机缺失假设。需要说明的是，这里所提到的随机缺失假设只是证明分析合理的假设，并不是数据的属性。

也就是说，如果填补模型中包含可预测相关协变量中缺失数据的变量，则随机缺失假设可能是合理的，但如果该变量从模型中省略，则不合理。

所以，为了满足这一假设，在插补模型中包含最后实质性分析中的所有变量（而不是只放入缺失的变量）是更为明智的。在计算可行的情况下，即便有些变量不出现在实质性分析中，如果能预测相关协变量缺失，还是可以加入模型中。

04 NHANES实际应用（基于单调缺失模式）

我是在一本SAS相关的多重填补书（获取方式见文末）上找到的例子。例子本身并不复杂，但却给NHANES中多重填补提供了极好的参考。

因为对例子有一些改编，我们介绍一下我们所用到数据集和最终目的。以我们之前教程常用的Analysis_data数据集为例，计算多重填补后不同性别1999-2002年家庭收入贫困比的均值。

在例子中，作者假设复杂抽样研究设计可以预测相关协变量的缺失，从而通过固定效应的方式将分层聚类的组合变量以及权重加入填补模型。

以上都是例子相关的一些背景知识。接下来我们按照是否在填补模型中加入分层聚类组合变量和权重分别给出相应的SAS代码和最后的结果比较。

首先是在填补模型中加入分层聚类组合变量和权重的SAS代码。代码中有相应注释，可帮助理解哦。

/*在填补模型中加入descode，权重*/
data Analysis_data_1;
  set Analysis_data;
  descode = sdmvstra*10 + sdmvpsu; /*构建分层聚类组合变量*/
run;


proc mi data = Analysis_data_1 nimpute=0;  /*查看缺失模式*/
var RIAGENDR RIDAGEYR RIDRETH1 descode WTINT4YR INDFMPIR;
run;


proc mi data = Analysis_data_1 nimpute = 5 seed = 41
out = imputation;  /*将组合变量和权重加入填补模型，以及可能影响INDFMPIR缺失的一些协变量，如年龄、性别、种族*/
class RIAGENDR RIDRETH1 descode;
monotone regression (INDFMPIR);
var RIAGENDR RIDRETH1 RIDAGEYR descode WTINT4YR
INDFMPIR;
run;


proc surveymeans data = imputation; /*均值计算*/
strata sdmvstra; cluster sdmvpsu; weight WTINT4YR;
by _imputation_;
domain RIAGENDR;
var INDFMPIR;
ods output domain = imputation_gender;
run;


proc sort data = imputation_gender;
by RIAGENDR _imputation_;
run;


proc mianalyze data = imputation_gender edf = 29; /*将5个数据集的结果进行汇总，自由度通过聚类数目-分层数目加以计算*/
by RIAGENDR; modeleffects mean; stderr stderr;
run;

↑

从图中可以看出缺失模式为单调缺失模式

然后是在填补模型中不加入分层聚类组合变量和权重的SAS代码。除未加入相应变量外，代码基本一致，大家参照上面的注释就好。

/*在填补模型中未加入descode，权重*/
proc mi data = Analysis_data_1 nimpute = 5 seed = 41
out = imputation;
class RIAGENDR RIDRETH1;
monotone regression (INDFMPIR);
var RIAGENDR RIDRETH1 RIDAGEYR INDFMPIR;
run;


proc surveymeans data = imputation;
strata sdmvstra; cluster sdmvpsu; weight WTINT4YR;
by _imputation_;
domain RIAGENDR;
var INDFMPIR;
ods output domain = imputation_gender;
run;


proc sort data = imputation_gender;
by varname RIAGENDR _imputation_;
run;


proc mianalyze data = imputation_gender edf = 29;
by varname RIAGENDR;
modeleffects mean;
stderr stderr;
run;

最后是两种方式的结果比较。

↑

结果汇总比较

其实从图片可以看出，加入复杂抽样设计相关变量并没有使点估计和置信区间产生显著改变，但是通过这一点去推断复杂抽样设计相关变量对相关协变量缺失毫无影响也是不合理的。

05 缺失比例对方法选择的影响

文献中也没有真正统一的截断值为方法选择提供参考。

Scheffer的观点是建议如果缺失比例不超过6%（也有不少文章建议是5%），可对有完整数据的受访者进行分析；缺失比例不超过10%，可采用单一填补；缺失比例在10%-25%，可采用更复杂的方法如多重填补。

随机对照临床试验也有学者提出标准，我截图供大家参考。

↑

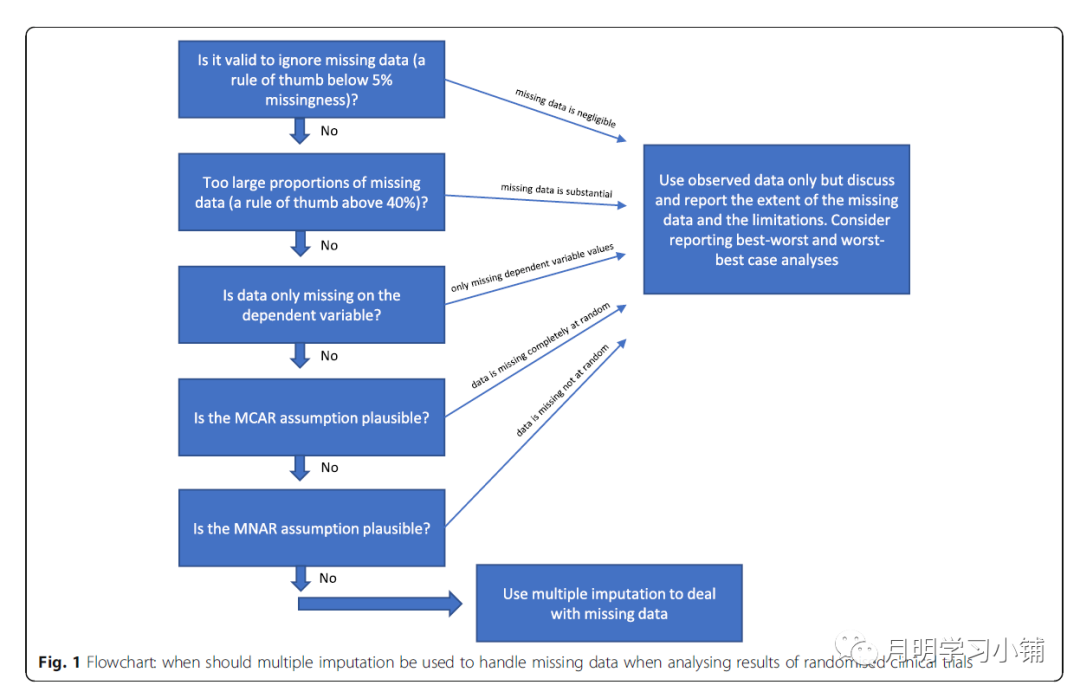
随机对照临床试验方法选择参考流程图

值得注意的是，有学者指出，除了缺失比例，缺失机制和缺失模式也是方法选择的重要参考。

06 一点总结

其实整篇推送我觉得最核心的内容是两个点，随机缺失假设和将复杂抽样设计相关变量加入填补模型。

这两个点并不是孤立的，而是相互佐证的。正是因为要尽可能满足随机缺失假设，本书的作者才会把复杂抽样设计相关变量加入填补模型；也正是因为加入了相关变量，才使得假设更为合理，之后分析造成的偏倚也更小。

没有人知道复杂抽样设计相关变量对相应协变量的缺失有多大影响。但其实我们心里都清楚，或多或少总有那么一点。

我觉得书里一句话真的将这一点解释的非常好，我也放在下面。

↑

大佬的对上述问题的解释

推文并不短，但相信看完的你一定会有些许收获。因为我在准备这篇推送的时候也受益匪浅。我对例子的内容有些许删减，有时间的话可以去看看我之前提到的那本SAS相关的多重填补书，后台回复imputation即可获取电子版，仅供学习交流使用哈~

记得点赞在看转发哦。祝好，科研顺利，周末愉快。炎热的夏天也不要忘记好好照顾自己。下下周五见~（我们下一期的内容应该会是复杂抽样中的中位数和秩和检验，有朋友问到，加上之前搞到一些资料，所以我们把这一期的内容往前调）

06 参考内容（部分）

Multiple Imputation of Missing Data Using SAS（文中提到书的书名）

[1]张桥,李宁,张秋菊,刘美娜.任意缺失模式缺失数据不同填补方法效果比较[J].中国卫生统计,2013,30(05):690-692.

Sterne JA, White IR, Carlin JB, et al. Multiple imputation for missing data in epidemiological and clinical research: potential and pitfalls. BMJ. 2009;338:b2393.

akobsen JC, Gluud C, Wetterslev J, Winkel P. When and how should multiple imputation be used for handling missing data in randomised clinical trials - a practical guide with flowcharts. BMC Med Res Methodol. 2017;17(1):162.