为什么Python 3.x里的round(2.5)等于2

众所周知，Python2.x和Python3.x版本在很多地方存在差异，不过有一处可能并没有受到太多人的关注：round()函数的行为。

在Python 2.x中，round()函数的机制是四舍五入，也符合大多数人的认知。

然而在Python 3.x版本中， round()函数的行为就会变得有些神奇。

Python 3.x中round(2.5) == 2
,而round(3.5) == 4
, 并没有遵从四舍五入的规则。事实上Python 3.x的文档是这样描述的：

For the built-in types supporting round(), values are rounded to the closest multiple of 10 to the power minus ndigits; if two multiples are equally close, rounding is done toward the even choice (so, for example, both round(0.5) and round(-0.5) are 0, and round(1.5) is 2). Any integer value is valid for ndigits (positive, zero, or negative). The return value is an integer if ndigits is omitted or None. Otherwise the return value has the same type as number.

可以看到，Python 3.x在处理类似round(2.5)的情况时，2.5与2和3的差值相等，都是0.5,此时会返回偶数，也就是2。对于round(3.5), 3.5与3和4的差值相等，返回偶数4。

虽然这种“四舍六入五成双”的规则比较奇怪，但Python 3.x的设计者的并不是脑洞大开才选择这样的实现方式，事实上这种舍入规则，也被称作高斯舍入(Gaussian rounding)和银行家舍入(bankers' rounding),是IEEE 754中的五种标准舍入规则之一。

银行舍入算法比起传统的四舍五入的优势在于更加均衡。举个例子，对于0.1
到0.9
九个数字，四舍五入保留整数的话0.1, 0.2, 0.3, 0.4
四个数字会舍为0
，而0.5, 0.6, 0.7, 0.8, 0.9
五个数字会入为1
，这其实是不平均的。

让我们考虑更多数字进来。

import math
floor = 0
ceil = 0
same = 0
for x in range(0,100):
    r = round(x/10.0)
if r == x/ 10.0:
   same += 1
if r == math.floor(x  10.0):
floor += 1
if r == math.ceil(x  10.0):
ceil += 1
print(same, floor, ceil)

这段代码统计了0.0
到9.9
共一百个数字round后舍(floor)，入(ceil)和保持不变(same)的数目。

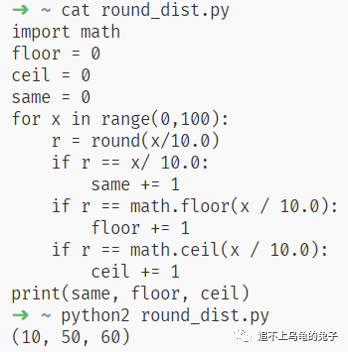
在Python 2.x中，因为逢五就入，所以ceil比floor大10, 在样本数量更大的情况下，这种不均衡也会被放大。

在Python 3.x中，ceil和floor大小就相同，即使在海量数据下，也不会产生不均衡的情况。鉴于Python在数据处理和分析领域的应用很广泛，选择更为均衡的round()函数实现也是应该的。

值得一提的是，很多编程语言都有内置的银行舍入算法的实现，在Java中就可以通过指定RoundingMode
选择不同的实现，其中HALF_EVEN
就是银行舍入算法。

BigDecimal bd = BigDecimal.valueOf(2.5d);
bd = bd.setScale(0, RoundingMode.HALF_EVEN); // bd == 2.0

以上就是Python 3.x版本round()函数与Python 2.x版本的不同，以及选用银行舍入算法背后的原因。