浅析 SQL 数据分析题目——统计连续完成数量

SQL干货分享 2021-08-13

1064

（CSDN博主：写代码也要符合基本法）

各位看官老爷大家早上好，我是你们的老伙计小刘，最近我其实工作挺忙的，但还是坚持看到了一道很有意思的分析题目，特此前来水一波

如上表所示的数据中，每个工人在某个时间序列中最多可能完成一件工作，要求我们把每个工人连续完成的工作件数计算累计数，逢 0 件重新计算，逢时序中断重新计算，期待的结果如下

从上面的结果我们可以看到，比如 SCOTT 的数据中，时序 1、5 和 6 分别完成了 0 件，所以累计计算在经过这些点后重新计算了

再如 YUSUF 的数据中，由于缺少时序 4，所以前后两个时序虽然完成件数都是 1，但是分别计算了累计件数

这道题目拿来一看，想必开窗函数（分析函数）是较优的选择，对于连续出现的 1 来说，累计前序行的数字即计算累计数量。而对于 0 件的记录来说，无论是单个出现的，还是连续出现的，反正累加起来还是 0，同样实现了“逢 0 件重新计算”的要求

所以说初步可以得出的思路是，不管是 0 是 1，分别累加即可

那么我们进一步要分析的就是，窗口的分组依据：首先“姓名”无疑是第一分组条件，第二点则是时序连续的记录分为一组，第三点则是在前两点基础上，再将连续出现的 0 或 1 分为一组（单独出现的自成一组）

从上面的分析中，我们最面熟的就是连续的时序数字分组这一条，因为之前分享的题目中有专门讨论过这种经典话题，详情回顾→传送门

接下来我们则暂时在时间序列连续的前提下讨论如何将连续出现的 0 或者 1 分为一组，这里我们单拿出 SCOTT 的数据加以讨论

将连续出现的、重复的数字分为一组，我想这应该也算得上是一个很具广泛意义的议题，解决方法应该有很多种，在这里小刘简单写一下我的思路

我们现有的数据是具有一列自己的序号的，那就是“时序”，那么当我们以时序排列数据后，“完成件数”这一列就变得“杂乱”：0 和 1 到处都是，自立山头

所以我们转换一下思路，站在“完成件数”的角度上观察：如果我们先把 0 和 1 的数据集合到各自的“阵营”，每个阵营中再按它们自带的时序来排列，那么在一个阵营中，时序连续的每组数据再追溯回原来不分阵营的情况中，自然还是连在一起的

至此，我们便实现了把未知问题转换成已知问题来处理（所以还不了解“连续数字分组”话题的小伙伴请一定先阅读之前的分享→传送门）

SQL> WITH sbq AS
  2   (SELECT time_seq
  3          ,complete_qty
  4          ,row_number() over(ORDER BY complete_qty, time_seq) rn
  5      FROM demo_completion
  6     WHERE ename = 'SCOTT')
  7  SELECT time_seq, complete_qty, time_seq - rn p FROM sbq ORDER BY time_seq;


  TIME_SEQ COMPLETE_QTY          P
---------- ------------ ----------
         1            0          0
         2            1         -2
         3            1         -2
         4            1         -2
         5            0          3
         6            0          3
         7            1          0
         8            1          0

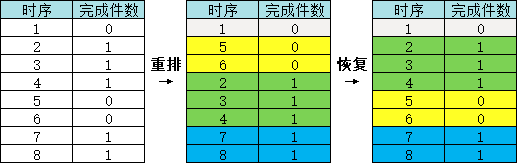
观察 P 列结果，我们发现：时序 2、3、4 的记录和 5、6 的记录已经被成功分离，但是 1 和 7、8 虽然完成件数不同，仍然 P 值相同，所以我们最终分组的依据还不能仅用 P 值，需要结合完成件数和 P 值来分组

SQL> WITH sbq AS
  2   (SELECT time_seq
  3          ,complete_qty
  4          ,time_seq - row_number() over(ORDER BY complete_qty, time_seq) p
  5      FROM demo_completion
  6     WHERE ename = 'SCOTT')
  7  SELECT time_seq
  8        ,complete_qty
  9        ,p
 10        ,SUM(complete_qty) over(PARTITION BY complete_qty, p ORDER BY time_seq) msum_cq
 11    FROM sbq
 12   ORDER BY time_seq;


  TIME_SEQ COMPLETE_QTY          P    MSUM_CQ
---------- ------------ ---------- ----------
         1            0          0          0
         2            1         -2          1
         3            1         -2          2
         4            1         -2          3
         5            0          3          0
         6            0          3          0
         7            1          0          1
         8            1          0          2

看到这里就有机谨的小伙伴要问了：难道能保证不会出现跨越分布的同值的“完成件数”小组对应一致的 P 值吗？出现这种情况不就将跨越分布的小组合到一起计算累计值了吗？

答案当然是肯定的，我在这里简单解释一下：假设出现在较前位置的完成 1 件的某行时序为 t1，对应 P 值为 p1，那么这一行在 1 阵营中的排序就是 (t1 - p1)

再设出现在较后位置的完成 1 件时序为 t2，对应 P 值为 p2，阵营内排序则为 (t2 - p2)

如果我们令 p1 = p2 = p，易得 t2 - t1 = (t2 - p) - (t1 - p)，即时序的距离等于阵营内排序的距离，也就是说按时序排列后，这两行之间不能出现其它阵营的记录

再说白一点：这两行必然位于同一个连续小组内

解决完这个小问题，我们再回到前面被我们跳过的关于时序数字判断连续的问题，不难发现我们已经在完成件数这个更细粒度的范围内判断过时序数字的连续了，那么“小连续”必定符合“大连续”，从而单纯判断时序连续的问题不需要考虑了

故此我们放眼到全表，则再加以姓名列分组即可

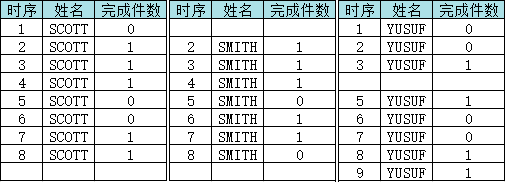
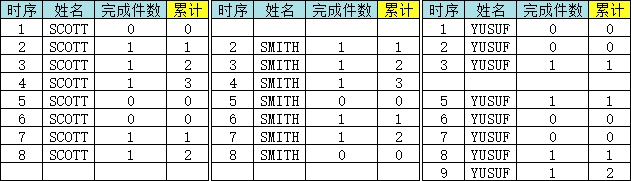
SQL> WITH sbq AS
  2   (SELECT time_seq
  3          ,ename
  4          ,complete_qty
  5          ,time_seq - row_number() over(PARTITION BY ename ORDER BY complete_qty, time_seq) p
  6      FROM demo_completion)
  7  SELECT time_seq
  8        ,ename
  9        ,complete_qty
 10        ,SUM(complete_qty) over(PARTITION BY ename, complete_qty, p ORDER BY time_seq) msum_cq
 11    FROM sbq
 12   ORDER BY ename, time_seq;


  TIME_SEQ ENAME COMPLETE_QTY    MSUM_CQ
---------- ----- ------------ ----------
         1 SCOTT            0          0
         2 SCOTT            1          1
         3 SCOTT            1          2
         4 SCOTT            1          3
         5 SCOTT            0          0
         6 SCOTT            0          0
         7 SCOTT            1          1
         8 SCOTT            1          2
         2 SMITH            1          1
         3 SMITH            1          2
         4 SMITH            1          3
         5 SMITH            0          0
         6 SMITH            1          1
         7 SMITH            1          2
         8 SMITH            0          0
         1 YUSUF            0          0
         2 YUSUF            0          0
         3 YUSUF            1          1
         5 YUSUF            1          1
         6 YUSUF            0          0
         7 YUSUF            0          0
         8 YUSUF            1          1
         9 YUSUF            1          2

数据库

文章转载自SQL干货分享，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

浅析 SQL 数据分析题目——统计连续完成数量

评论