如何理解分治算法
什么是分治算法?简单来说就是“分而治之”,也就是将原问题划分成n个规模较小的,并且结构与原问题相似的子问题,然后去递归地解决这些子问题,最后再合并其结果,就得到原问题的解。
对于分治算法来说,一般适合用递归来实现。分治算法的递归实现中,每一次递归都会涉及如下三个操作。
分解:将原问题分解成一系列子问题。
解决:递归地求解各个子问题。
合并:将子问题的结果合并成原问题。
分治算法的问题模型
对于可以采用分治算法来解决的问题,一般都需要满足以下几个条件:
原问题与分解成的子问题具有相同的模式。
原问题分解成的子问题可以独立求解,子问题之间没有相关性。
具有分解终止条件,也就是说,当问题足够小时,可以直接求解。
可以将子问题合并成原问题,而这个合并操作的复杂度不能太高,否则就起不到减小算法总体复杂度的效果了。
下面我们来结合一个例子来看一下分治算法的应用。我们来思考这么一个问题,在给定一组在二维空间中的n个点,如何快速找出距离最近的两点呢?
最直观的想法就是通过遍历所有的点,然后求出所有点之间的距离,最后选出这些距离中的最小值对应的点,但是这种算法的时间复杂度是O(n*n),那有没有更快的方法呢?那就是分治算法。
为了方便起见,我们把N设置为2的k次幂,即N=2^k,k为正整数。下面我们来看一下这个问题是否满足分治算法的问题模型。
我们可以把问题N拆分成两个子问题,每个子问题等于原问题的一半。我们在二维平面中画一条垂线e,正好把N个点按照x轴位置拆分成2半(这个过程需要按照x轴排序,取中间的点),使得e的左右两边都有n/2个点。假设我们对e的左半边部分递归的求出的最近点对的距离为ld,e的右半边部分递归的求出的最近点对的距离为rd,接下来我们取出这两个距离中的最小值d=min(ld,rd),并且在e-d和e+d的位置上画两条垂线。这样一来,我们把二维空间划分成了3部分。如下图所示:
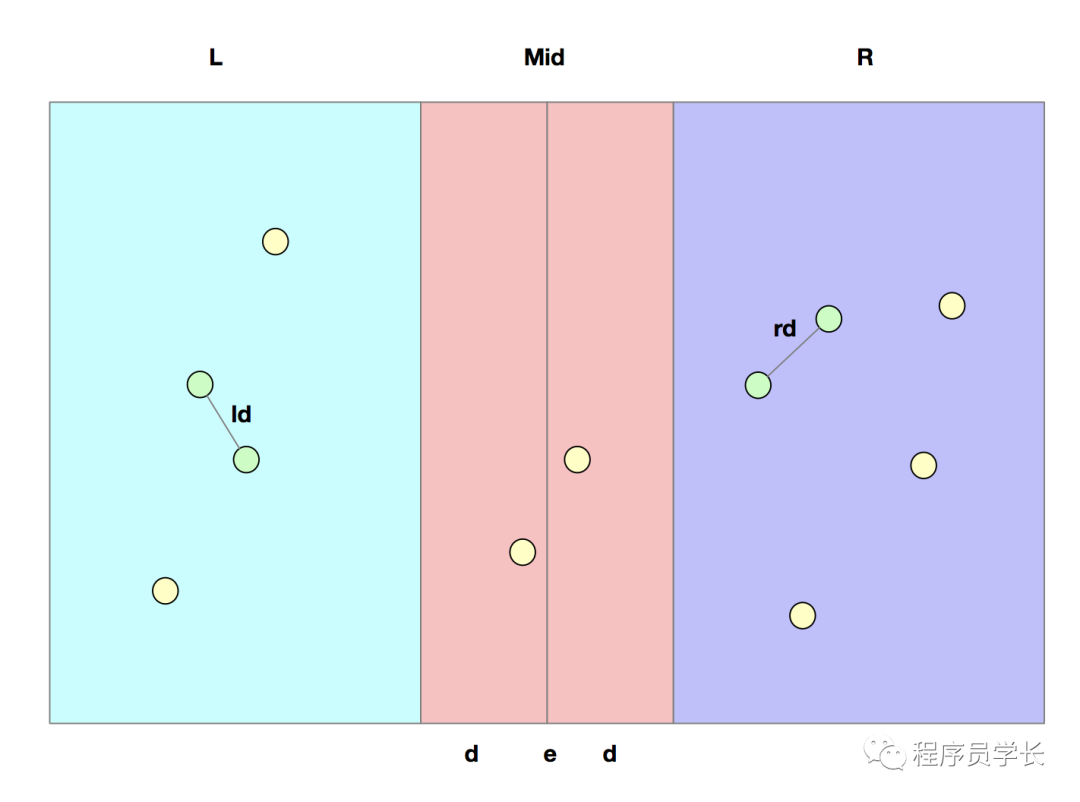
这样划分后,最近点对的出现位置只能有以下三种可能。
两个节点都在左边区域。
一个节点在左,一个节点在右。
两个节点都在右边。
其中,1和3我们已经在求解子问题的时候已经解决了,现在我们只需要求解第2个问题就好了,即在mid区域进行搜索。我们下面来看如何在mid区域进行搜索,我们需要把这个带状区域内的所有节点按照Y轴递增排序(我们可以在初始化的时候就缓存起来,后面直接使用就好),从Y排序最小的节点开始,我们连续检查带状区域内的每个点,计算所有比它的Y轴更大的点之间的距离,尝试找出距离比d更小的点对。
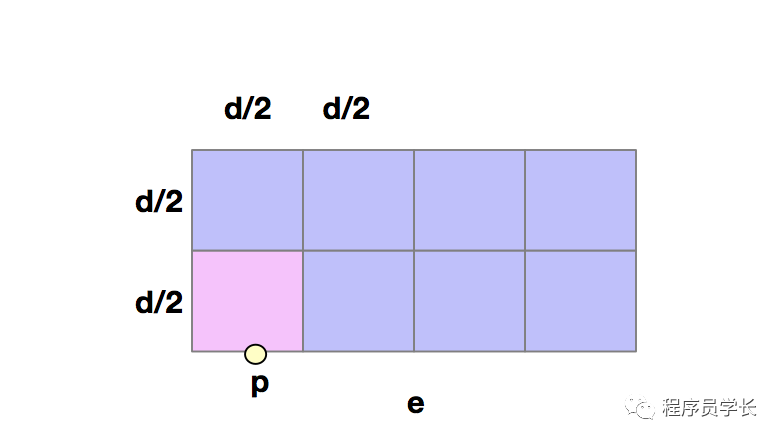
假设我们需要对节点p进行比较,我们考虑这样的一个空间,他是通过8个正方形(d/2*d/2)组成的一个长方形,p节点位于这个长方形的底边上,
我们只需要判断这个区域内的所有节点即可,因为一旦Y轴差距超过了d,就算x轴之差为0也会大于我们之前的距离d,所以不可能找出比 d 距离更小的点对。并且我们针对一个点,事实上只需要最多对比 7 次就能找出所有可能小于 d 的点对,因为每个小格子内部只可能出现1个节点,因为小格子内部的极限距离为 d sqrt(2),也就是正方形的对角线,但是这个距离显然小于 d,如果这个正方形内部存在这样一个节点。那么之前对于 d 是左右区域内最小的点对距离的定义就被破坏了。所以不可能存在。
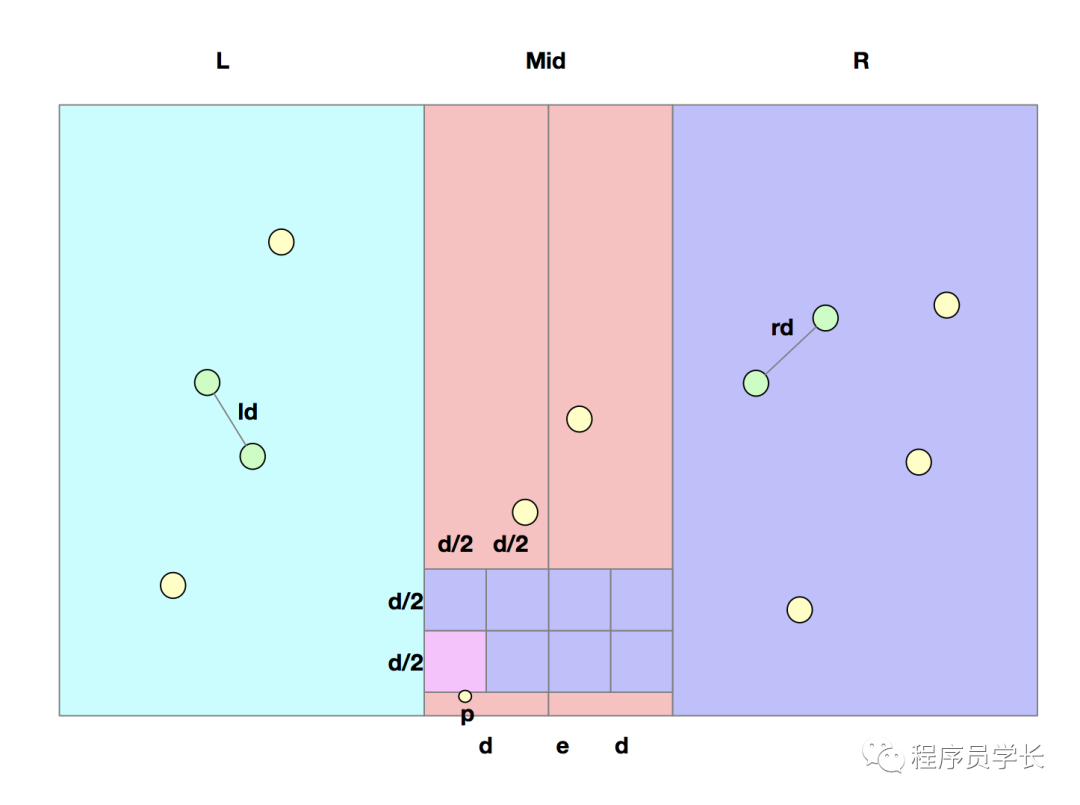
综上所述:这个问题是符合分治算法的问题模型的。下面我们来看一下代码实现。
import mathclass Point:def __init__(self,x,y):self.x=xself.y=ydef __str__(self):return 'x='+str(self.x)+',y='+str(self.y)class RecentPoint:sortByXPoints = []sortByYPoints = []# p1=None# p2=Nonedef getDistance(self, p1, p2):xDis = (p1.x - p2.x) ** 2yDis = (p1.y - p2.y) ** 2return math.sqrt(xDis + yDis)def findRecentPoint(self,data):#可以采用快速排序算法,时间复杂度为O(nlogn)self.sortByXPoints=sorted(data,key=lambda point:point.x)self.sortByYPoints=sorted(data,key=lambda point:point.y)return self._findRecentPoint(0, len(data)-1)def _findRecentPoint(self, p, q):#区域内只有两对节点if (q-p)<=1:return self.getDistance(self.sortByXPoints[p], self.sortByXPoints[q])middle=math.floor((p+q)/2)ld=self._findRecentPoint(p, middle)rd=self._findRecentPoint(middle+1, q)# if(ld<rd):# d=ld# self.p1 = self.sortByXPoints[p]# self.p2 = self.sortByYPoints[middle]# else:# d = rd# self.p1 = self.sortByXPoints[middle+1]# self.p2 = self.sortByYPoints[q]d=min(ld,rd)#中心点e=self.sortByXPoints[middle].x + (self.sortByXPoints[middle+1].x - self.sortByXPoints[middle].x) 2LeftEdge = e - dRightEdge = e + d#接下来我们检查已 X 轴坐标 e 为中心点 从 e - d 开始 e + d 结束的带状区域内去检测最近点#我们从中筛选所有带状区域内的点,并按照 Y坐标 的递增排序进行排序insidePoint=[]for point in self.sortByYPoints:if(point.x>LeftEdge and point.x<RightEdge):insidePoint.append(point)#开始对比节点,寻找是否比d更短for i in range(len(insidePoint)):for j in range(1,8):if(i+j>=len(insidePoint)):break;dis=self.getDistance(insidePoint[i],insidePoint[i+j])if(dis<d):d=dis# self.p1=insidePoint[i]# self.p2=insidePoint[i+j]return ddata=[Point(1,6),Point(3, 4),Point(2, 5),Point(4, 8)]s=RecentPoint()print(s.findRecentPoint(data))# print(s.p1)# print(s.p2)#通过分析代码f(n)=f(n/2)+7n,所以时间复杂度是O(nlogn)
更多有趣知识,请关注公众号。
觉得不错,点个“在看”吧,谢谢
新规则,及时看推文要给公号“星标”,
不然就错过了~






