ICDE2023_Robust Attributed Graph Alignment via Joint Structure Learning and Optimal Transport_腾讯云数据库.pdf

tinge

100

14页

3次

2023-08-29

免费下载

Robust Attributed Graph Alignment via Joint

Structure Learning and Optimal Transport

Jianheng Tang

2†

, Weiqi Zhang

, Jiajin Li

, Kangfei Zhao

, Fugee Tsung

1,2

, Jia Li

1,2∗

Hong Kong University of Science and Technology (Guangzhou),

Hong Kong University of Science and Technology,

Stanford University,

Tencent AI Lab

{jtangbf,wzhangcd}@connect.ust.hk, jiajinli@stanford.edu, zkf1105@gmail.com, {season,jialee}@ust.hk

Abstract—Graph alignment, which aims at identifying cor-

responding entities across multiple networks, has been widely

applied in various domains. As the graphs to be aligned are usu-

ally constructed from different sources, the inconsistency issues

of structures and features between two graphs are ubiquitous

in real-world applications. Most existing methods follow the

“embed-then-cross-compare” paradigm, which computes node

embeddings in each graph and then processes node correspon-

dences based on cross-graph embedding comparison. However,

we ﬁnd these methods are unstable and sub-optimal when

structure or feature inconsistency appears. To this end, we

propose SLOTAlign, an unsupervised graph alignment frame-

work that jointly performs Structure Learning and Optimal

Transport Alignment. We convert graph alignment to an optimal

transport problem between two intra-graph matrices without the

requirement of cross-graph comparison. We further incorporate

multi-view structure learning to enhance graph representation

power and reduce the effect of structure and feature inconsistency

inherited across graphs. Moreover, an alternating scheme based

algorithm has been developed to address the joint optimization

problem in SLOTAlign, and the provable convergence result is

also established. Finally, we conduct extensive experiments on

six unsupervised graph alignment datasets and the DBP15K

knowledge graph (KG) alignment benchmark dataset. The pro-

posed SLOTAlign shows superior performance and strongest

robustness over seven unsupervised graph alignment methods

and ﬁve specialized KG alignment methods.

Index Terms—Graph alignment, Unsupervised learning, Struc-

ture learning, Optimal transport

I. INTRODUCTION

Graph alignment refers to the problem of identifying the

node correspondences (i.e., anchor links) across different

graphs. With graph data becoming ubiquitous in the Web

era, graph alignment establishes connections between multiple

networks and integrates them into a world-view network for

subsequent analysis and downstream applications. Thus, graph

alignment provides a comprehensive perspective for structured

data compared with mining each individual network. As a

well-established problem, graph alignment has received much

attention due to its vast applicable tasks, e.g., linking accounts

in different social network platforms [25], [26], [40], matching

entities across different knowledge graphs [34], [45], [63],

∗

Corresponding author.

†

Work done during an internship at Tencent AI Lab.

Code and data are released at https://github.com/squareRoot3/SLOTAlign

[69], integrating protein-protein interactions of different species

[21], [35], merging scholar proﬁles of academic collaboration

networks [47], [67].

Graph alignment is usually treated as a supervised problem

[33], [36], [67], [68], in which a set of ground-truth node

correspondences is given. However, these correspondences

are usually unavailable and further suffer from the labor

expensiveness issue in real-world applications. Thus, unsu-

pervised graph alignment methods have attracted increasing

attention [4], [9], [14], [17], [19], [31], [72]. Also, graph

nodes are often associated with wealthy side information,

such as the user information of social network accounts

or the embedding of knowledge graph entities. These high-

dimensional node features/attributes can serve as an additional

source of knowledge in graph alignment, especially under the

unsupervised setting.

Most existing graph alignment methods rely on high-quality

and well-measured graph structures. They require that the

structure of the overlapped parts between two graphs is similar,

which is named structure consistency thereafter. However, real-

world graphs are often coupled with outliers [46] or with

missing/irrelevant edges [28], [54], [61], leading to structure

inconsistency across graphs. It is often observed that the same

entities in different networks have quite different neighbors

due to the structural noise [4], [72]. Figure 1 demonstrates an

example of graph alignment on two social network platforms.

Black dashed lines are anchor links that connect the same copies

of users across two networks. As can be seen, two circled nodes

are connected on Platform A, but their corresponding nodes

on Platform B are not connected.

Besides structure inconsistency, another largely overlooked

issue is that node features in different graphs are usually

unaligned and inconsistent. Due to various functionalities of

different networks (e.g., LinkedIn for job seeking and Twitter

for opinion sharing), the same user in different networks

commonly does not share the same features. Taking Figure 1

as an example, user information in Platform A includes the real

name, gender, and education experiences, while Platform B

contains the anonymized username, locations, posts, etc. Under

this situation, corresponding nodes across two networks are

not similar to each other and are incomparable. Likewise, in

cross-lingual knowledge graph alignment, entities in different

arXiv:2301.12721v2 [cs.DB] 20 Apr 2023

Platform A

Structure

Inconsistency

Username

Locations

Posts

…

Platform B

Name

Gender

Education

…

Corresponding

Nodes

Feature

Inconsistency

Fig. 1. An example of graph alignment with structure and feature inconsistency.

languages are usually embedded into individual feature spaces.

Using machine translation [37], [44] can alleviate this issue,

but may bring additional noise and cost.

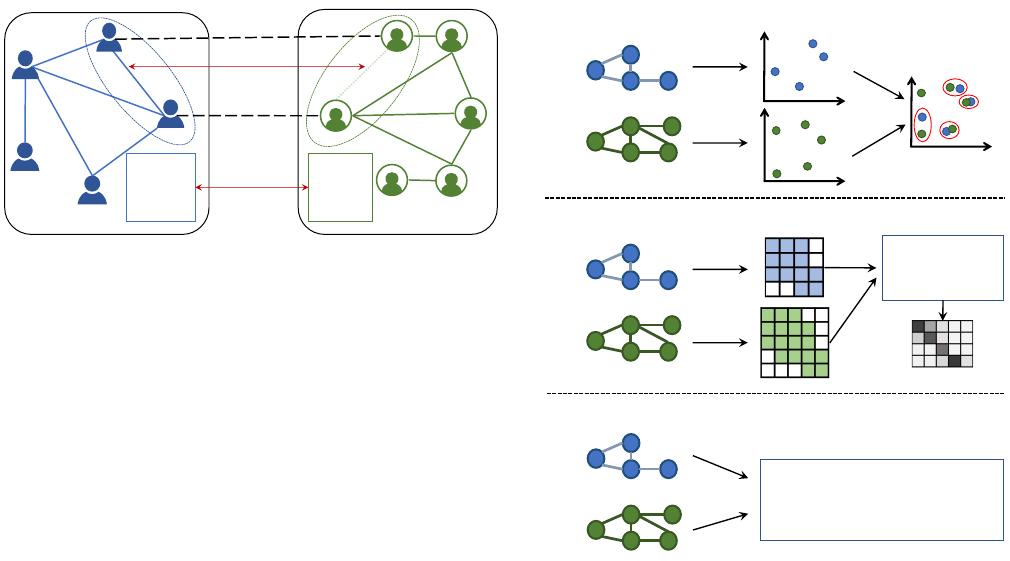
In previous works, a popular paradigm for unsupervised

graph alignment is the “embed-then-cross-compare” procedure

[4], [9], [14], [17], [23], [31], as shown in Figure 2(a).

As the name suggests, it ﬁrst embeds nodes in each graph

into a common feature space (e.g., using a graph neural

network), and then compares embeddings across two graphs

to obtain node correspondences. Nonetheless, we ﬁnd this

paradigm has the following limitations to deal with structure

and feature inconsistency. First, as the node embeddings are

calculated by aggregating information from the neighbors, it

may amplify noise when structure inconsistency exists. Second,

if features in two graphs are inconsistent, the corresponding

node embeddings are also typically inconsistent and can not

be compared directly [5], [14]. In knowledge graph alignment,

margin-based ranking losses [44], [45] and contrastive learning

[63] are frequently used to integrate embedding spaces across

graphs. However, without the supervision of ground-truth node

pairs, the process of embedding space integration is unstable

and unreliable.

Besides the “embed-then-cross-compare” paradigm, another

line of research is to reformulate the graph alignment problem

as ﬁnding the optimal probabilistic correspondence between

two probability measures on graphs. Speciﬁcally, Gromov-

Wasserstein (GW) distance serves as an effective tool in

modeling the correspondence problems between two graphs on

unaligned metric spaces [30], [43]. We show the procedure of

the resulting optimal transport based alignment in Figure 2(b). It

ﬁrst constructs two cost matrices

and

within each graph.

Then, it applies an optimal transport solver to ﬁnd the best

transportation plan

with minimal cost according to

and

. The transportation plan

reveals node correspondences

across graphs.

However, previous optimal transport based methods mainly

consider the alignment between plain graphs without attributes

and rely on manually designed cost matrices (e.g., the original

graph adjacency matrix [30], [58], [60] or the heat kernel of

graph Laplacian matrix [1], [6], [27]). Thus, these methods

are potentially fragile to structure inconsistency. Moreover,

how to ﬁnd optimal cost matrices in attributed graphs for the

optimal transport based alignment has not been well explored

by existing methods. In summary, there is no satisfactory

𝓖

𝑡

𝓖

𝑠

Embed

Cross-Compare

𝓖

𝑡

𝓖

𝑠

Cost Matrix

OT Solver

𝑫

𝑠

𝑫

𝒕

min 𝑓(𝜋, 𝑫

𝑠

, 𝑫

𝒕

)

𝜋

𝓖

𝑡

𝓖

𝑠

Joint Optimization Scheme

min 𝑓(𝜋, 𝑫

𝑠

, 𝑫

𝒕

)

𝜋, 𝑫

𝑠

, 𝑫

𝒕

(a) The “Embed-Then-Cross-Compare” Alignment Paradigm

(b) Optimal Transport Based Alignment

𝜋

Fig. 2. Comparison between the existing graph alignment methods (top and

middle) and our proposed SLOTAlign framework (bottom).

solution for enhancing the robustness of graph alignment

against structure and feature inconsistency.

To address above issues, we propose a novel framework

for joint Structure Learning and Optimal Transport Alignment

(SLOTAlign). As shown in Figure 2(c), SLOTAlign simul-

taneously optimizes the intra-graph structure representation

(

, D

) and cross-graph transportation plan

in a uniﬁed

manner, which can get rid of choosing cost matrices manually.

SLOTAlign models the multi-view structure representation

within each graph, which integrates the node-view, edge-view,

and subgraph-view to reduce the effect of noise and incon-

sistency in original graph structures. Moreover, SLOTAlign

is more robust to feature inconsistency as it only utilizes

intra-graph node relation and does not depend on cross-

graph node embedding comparison. Additionally, we show

that SLOTAlign is invariant to graph feature permutation,

which cannot be achieved by the “embed-then-cross-compare”

methods. Theoretically, we provide an alternating scheme

based algorithm to address the optimization problem arisen

from SLOTAlign, and establish the convergence result of the

proposed algorithm.

To sum up, our contributions are three-fold:

●

We point out and analyze that existing attributed graph

alignment methods are susceptible to both structure and

feature inconsistency, and thus perform unstably in noisy

real-world graphs.

●

A novel framework — SLOTAlign has been proposed for

joint structure learning and optimal transport alignment.

We prove the robustness guarantee of SLOTAlign against

of 14

免费下载

关注

评论