SCALEFORMER ITERATIVE MULTI-SCALE REFINING.pdf

smith0907

555

23页

0次

2023-10-24

50墨值下载

Published as a conference paper at ICLR 2023

SCALEFORMER: ITERATIVE MULTI-SCALE REFINING

TRANSFORMERS FOR TIME SERIES FORECASTING

Mohammad Amin Shabani,

Simon Fraser University, Canada

& Borealis AI, Canada

mshabani@sfu.ca

Amir Abdi, Lili Meng, Tristan Sylvain

Borealis AI, Canada

{firstname.lastname}@borealisai.com

ABSTRACT

The performance of time series forecasting has recently been greatly improved by

the introduction of transformers. In this paper, we propose a general multi-scale

framework that can be applied to the state-of-the-art transformer-based time series

forecasting models (FEDformer, Autoformer, etc.). By iteratively reﬁning a fore-

casted time series at multiple scales with shared weights, introducing architecture

adaptations, and a specially-designed normalization scheme, we are able to achieve

signiﬁcant performance improvements, from

5.5%

38.5%

across datasets and

transformer architectures, with minimal additional computational overhead. Via

detailed ablation studies, we demonstrate the effectiveness of each of our contri-

butions across the architecture and methodology. Furthermore, our experiments

on various public datasets demonstrate that the proposed improvements outper-

form their corresponding baseline counterparts. Our code is publicly available in

https://github.com/BorealisAI/scaleformer.

1 INTRODUCTION

Coarse ForecastingFine Forecasting

Time

Value

GroundTruth

Prediction

GroundTruth

Prediction

GroundTruth

Prediction

GroundTruth

Prediction

100 150 200

100

0 10 20 30

40 50

0 5 10 15 20 25

0.5

0.0

-0.5

-1.0

-1.5

0.5

0.0

-0.5

-1.0

-1.5

0.5

0.0

-0.5

-1.0

-1.5

0.0

-0.2

-0.5

-0.6

-0.8

-1.0

-1.2

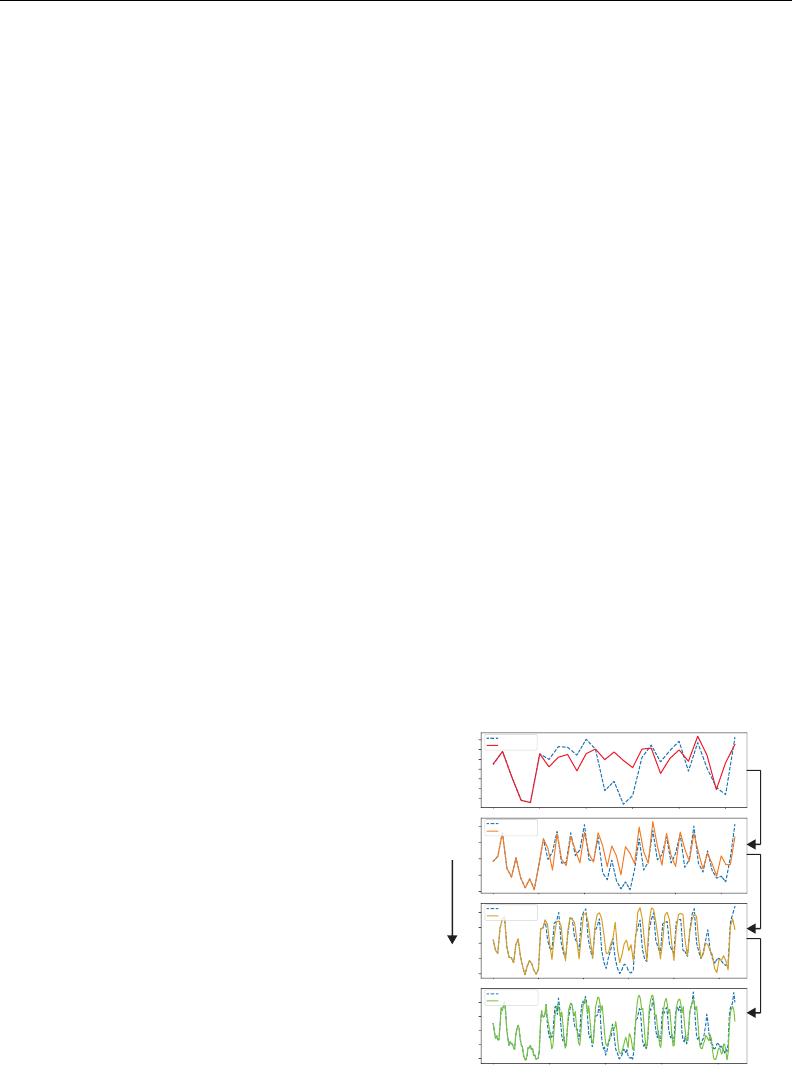
Figure 1: Intermediate forecasts by our model

at different time scales. Iterative reﬁnement

of a time series forecast is a strong structural

prior that beneﬁts time series forecasting.

Integrating information at different time scales is es-

sential to accurately model and forecast time series

(Mozer, 1991; Ferreira et al., 2006). From weather

patterns that ﬂuctuate both locally and globally, as

well as throughout the day and across seasons and

years, to radio carrier waves which contain relevant

signals at different frequencies, time series forecast-

ing models need to encourage scale awareness in

learnt representations. While transformer-based ar-

chitectures have become the mainstream and state-

of-the-art for time series forecasting in recent years,

advances have focused mainly on mitigating the stan-

dard quadratic complexity in time and space, e.g.,

attention (Li et al., 2019; Zhou et al., 2021) or struc-

tural changes (Xu et al., 2021; Zhou et al., 2022b),

rather than explicit scale-awareness. The essential

cross-scale feature relationships are often learnt im-

plicitly, and are not encouraged by architectural priors

of any kind beyond the stacked attention blocks that

characterize the transformer models. Autoformer (Xu

et al., 2021) and Fedformer (Zhou et al., 2022b) introduced some emphasis on scale-awareness by

enforcing different computational paths for the trend and seasonal components of the input time

series; however, this structural prior only focused on two scales: low- and high-frequency components.

Given their importance to forecasting, can we make transformers more scale-aware?

We enable this scale-awareness with Scaleformer. In our proposed approach, showcased in Figure 1,

time series forecasts are iteratively reﬁned at successive time-steps, allowing the model to better

capture the inter-dependencies and speciﬁcities of each scale. However, scale itself is not sufﬁcient.

Iterative reﬁnement at different scales can cause signiﬁcant distribution shifts between intermediate

arXiv:2206.04038v4 [cs.LG] 7 Feb 2023

Published as a conference paper at ICLR 2023

forecasts which can lead to runaway error propagation. To mitigate this issue, we introduce cross-scale

normalization at each step.

Our approach re-orders model capacity to shift the focus on scale awareness, but does not fundamen-

tally alter the attention-driven paradigm of transformers. As a result, it can be readily adapted to

work jointly with multiple recent time series transformer architectures, acting broadly orthogonally

to their own contributions. Leveraging this, we chose to operate with various transformer-based

backbones (e.g. Fedformer, Autoformer, Informer, Reformer, Performer) to further probe the effect

of our multi-scale method on a variety of experimental setups.

Our contributions are as follows: (1) we introduce a novel iterative scale-reﬁnement paradigm that

can be readily adapted to a variety of transformer-based time series forecasting architectures. (2) To

minimize distribution shifts between scales and windows, we introduce cross-scale normalization on

outputs of the Transformer. (3) Using Informer and AutoFormer, two state-of-the-art architectures, as

backbones, we demonstrate empirically the effectiveness of our approach on a variety of datasets.

Depending on the choice of transformer architecture, our mutli-scale framework results in mean

squared error reductions ranging from

5.5%

38.5%

. (4) Via a detailed ablation study of our

ﬁndings, we demonstrate the validity of our architectural and methodological choices.

2 RELATED WORKS

Time-series forecasting

: Time-series forecasting plays an important role in many domains, including:

weather forecasting (Murphy, 1993), inventory planning (Syntetos et al., 2009), astronomy (Scargle,

1981), economic and ﬁnancial forecasting (Krollner et al., 2010). One of the speciﬁcities of time

series data is the need to capture seasonal trends (Brockwell & Davis, 2009). There exits a vast variety

of time-series forecasting models (Box & Jenkins, 1968; Hyndman et al., 2008; Salinas et al., 2020;

Rangapuram et al., 2018; Bai et al., 2018; Wu et al., 2020). Early approaches such as ARIMA (Box

& Jenkins, 1968) and exponential smoothing models (Hyndman et al., 2008) were followed by the

introduction of neural network based approaches involving either Recurrent Neural Netowkrs (RNNs)

and their variants (Salinas et al., 2020; Rangapuram et al., 2018; Salinas et al., 2020) or Temporal

Convolutional Networks (TCNs) (Bai et al., 2018).

More recently, time-series Transformers (Wu et al., 2020; Zerveas et al., 2021; Tang & Matteson,

2021) were introduced for the forecasting task by leveraging self-attention mechanisms to learn

complex patterns and dynamics from time series data. Informer (Zhou et al., 2021) reduced quadratic

complexity in time and memory to

O(L log L)

by enforcing sparsity in the attention mechanism

with the ProbSparse attention. Yformer (Madhusudhanan et al., 2021) proposed a Y-shaped encoder-

decoder architecture to take advantage of the multi-resolution embeddings. Autoformer (Xu et al.,

2021) used a cross-correlation-based attention mechanism to operate at the level of subsequences.

FEDformer (Zhou et al., 2022b) employs frequency transform to decompose the sequence into

multiple frequency domain modes to extract the feature, further improving the performance of

Autoformer.

Multi-scale neural architectures

: Multi-scale and hierarchical processing is useful in many domains,

such as computer vision (Fan et al., 2021; Zhang et al., 2021; Liu et al., 2018), natural language

processing (Nawrot et al., 2021; Subramanian et al., 2020; Zhao et al., 2021) and time series

forecasting (Chen et al., 2022; Ding et al., 2020). Multiscale Vision Transformers (Fan et al., 2021)

is proposed for video and image recognition, by connecting the seminal idea of multiscale feature

hierarchies with transformer models, however, it focuses on the spatial domain, specially designed

for computer vision tasks. Cui et al. (2016) proposed to use different transformations of a time series

such as downsampling and smoothing in parallel to the original signal to better capture temporal

patterns and reduce the effect of random noise. Many different architectures have been proposed

recently (Chung et al., 2016; Che et al., 2018; Shen et al., 2020; Chen et al., 2021) to improve RNNs

in tasks such as language processing, computer vision, time-series analysis, and speech recognition.

However, these methods are mainly focused on proposing a new RNN-based module which is not

applicable to transformers directly. The same direction has been also investigated in Transformers,

TCN, and MLP models. Recent work Du et al. (2022) proposed multi-scale segment-wise correlations

as a multi-scale version of the self-attention mechanism. Our work is orthogonal to the above methods

of 23

50墨值下载

关注

评论