




使用衍射深度神经网络的全光机器学习.pdf
免费下载

OPTICAL COMPUTING
All-optical machine learning using
diffractive deep neural networks
Xing Lin
1,2,3
*, Yair Rivenson
1,2,3
*, Nezih T. Yardimci
1,3
, Muhammed Veli
1,2,3
,
Yi Luo
1,2,3
, Mona Jarrahi
1,3
, Aydogan Ozcan
1,2,3,4
†
Deep learning has been transforming our ability to execute advanced inference tasks using
computers. Here we introduce a physical mechanism to perform machine learning by
demonstrating an all-optical diffractive deep neural network (D
2
NN) architecture that can
implement various functions following the deep learning–based design of passive
diffractive layers that work collectively. We created 3D-printed D
2
NNs that implement
classification of images of handwritten digits and fashion products, as well as the function
of an imaging lens at a terahertz spectrum. Our all-optical deep learning framework can
perform, at the speed of light, various complex functions that computer-based neural
networks can execute; will find applications in all-optical image analysis, feature detection,
and object classification; and will also enable new camera designs and optical components
that perform distinctive tasks using D
2
NNs.
D
eep learning is one of the fastest-growing
machine learning methods (1). This ap-
proach uses multilayered artificial neural
networks implemented in a computer to
digitally learn data representation and ab-
straction and to perform advanced tasks in a
manner comparable or even superior to the per-
formance of human experts. Recent examples in
which deep learning has made major advances in
machine learning include medical image analysis
(2), speech recognition (3), language transla-
tion (4), and image classification (5), among others
(1, 6). Beyond some of these mainstream appli-
cations, deep learning methods are also being
used to solve inverse imaging problem s (7–13).
Here we introduce an all-optical deep learning
framework in which the neural network is phys-
ically formed by multiple layers of diffractive
surfaces that work in collaboration to optically
perform an arbitrary function that the network
can statistically learn. Whereas the inference and
prediction mechanism of the physical network
is all optical, the learning part that leads to its
design is done through a computer. We term this
framework a diffractive deep neural network
(D
2
NN) and demonstrate its inference capabil-
ities through both simulations and experiments.
Our D
2
NN can be physically created by using
several transmissive and/or reflective layers (14),
where each point on a given layer either trans-
mits or reflects the incoming wave, representing
an artificial neuron that is connected to other
neurons of the following layers through optical
diffraction(Fig.1A).Inaccordancewiththe
Huygens-Fresnel principle, our terminolog y is
based on each point on a given layer acting as a
secondary source of a wave, the amplitude and
phase of which are determined by the product
of the input wave and the complex-valued trans-
mission or reflection coefficient at that point [see
(14) for an analysis of the waves within a D
2
NN].
Therefore, an artificial neuron in a D
2
NN is con-
nected to other neurons of the following layer
through a secondary wave modulated in ampli-
tude and phase by both the input interference
pattern created by the earlier layers and the local
transmission or reflection coefficient at that point.
As an analogy to standard deep neural networks
(Fig. 1D), one can consider the transmission or
reflection coefficient of each point or neuron as
amultiplicative“bias” term, which is a learnable
network parameter that is iteratively adjusted
during the training process of the diffractive net-
work, using an error back-propagation method.
After this num erical training phase, th e D
2
NN
design is fixed and the transmission or reflec-
tion coefficients of the neurons of all layers are
determined. This D
2
NN design—once physically
fabricated using techniques such as 3D-printing
or lithography—can then perform, at the speed
of light, the specific task for which it is trained,
using only optical diffraction and passive optical
components or layers that do not need po wer,
thereby creating an efficient and fast way of
implementing machine learning tasks.
In general, the ph ase and amplitude of ea ch
neuron can be learnable parameters, providing
a complex-valued modulation at each layer,
which improves the inference performance of
the diffractive network (fig. S1) (14). For coher-
ent transmissive networks with phase-only mod-
ulation, each layer can be approximated as a thin
optical element (Fig. 1). Through deep learning,
the phase values of the neurons of each layer of
the diffractive network are iteratively adjusted
(trained) to perform a specific function by feed-
ing training data at t he input layer and then
computing the network’s output through optical
diffraction. On the basis of the calculated error
with respect to the target output, determined by
the desired function, the network structure and
its neuron phase values are optimized via an error
back-propagation algorithm, which is based on
the stochastic gradient descent approach used
in conventional deep learning (14 ).
To demonstrate the performance of the D
2
NN
framework, we first trained it as a digit classifier
to perform automated classification of hand-
written digits, from 0 to 9 (Figs. 1B and 2A). For
this task, phase-only transmission masks were
designed by training a five-layer D
2
NN with
55,000 images (5000 validation images) from the
MNIST (Modified National Institute of Stan-
dards and Technology) handwritten digit data-
base (15). Input digits were encoded into the
amplitude of the i nput field to the D
2
NN, and
the diffractive network was trained to map input
digits into 10 detector regions, one for each digit.
The classification criterion was to find the de-
tector with the maximum optical signal, and this
was also used as a loss function during the net-
work training (14).
After training, the design of the D
2
NN digit
classifier was numer ically tested using 10,000
images from the MNIST test dataset (which were
not used as part of the training or validation
image sets) and achieved a classification accu-
racy of 91.75% (Fig. 3C and fig. S1). In addition to
the classification performance of the diffractive
network, we also analyzed the energy distribu-
tion observed at the network output plane for the
same 10,000 test digits (Fig. 3C), the results of
which clearly demonstrate that the diffractive
network learned to focus the input energy of
each handwritten digit into the correct (i.e., the
target) detector region, in accord with its train-
ing. With the use of complex-valued modulation
and increasing numbers of layers, neurons, and
connections in the diffractive network, our classi-
fication accuracy can be further improved (figs.
S1 and S2). For example, fig. S2 demonstrates a
Lego-like physical transfer learning behavior for
D
2
NN framework, where the inference perform-
ance of an already existing D
2
NN can be further
improved by adding new diffractive layers—or, in
some cases, by peeling off (i.e., discarding) some
of the existing layers—where the new layers to
be added are trained for improved inference
(coming from the entire diffractive network: old
and new layers). By using a patch of two layers
added to an existing and fixed D
2
NN design (N =
5 layers), we improved our MNIST classification
accuracy to 93.39% (fig. S2) (14); the state-of-the-
art convolutional neural network performance
has been reported as 99.60 to 99.77% (16–18).
More discussion on reconfiguring D
2
NN designs
is provided in the supplementary materials (14).
Following these numerical results, we 3D-
printed our five- layer D
2
NN design (Fig. 2A),
with each layer having an area of 8 cm by 8 cm,
followed by 10 detector regions defined at the
output plane of the diffractive network (Figs. 1B
and 3A). We then used continuous-wave illumi-
nation at 0.4 THz to test the network’sinference
performance (Figs. 2, C and D). Phase values of
RESEARCH
Lin et al., Science 361, 1004–1008 (2018) 7 September 2018 1of5
1
Department of Electrical and Computer Engineering, University
of California, Los Angeles, CA 90095, USA.
2
Department
of Bioengineering, University of California, Los Angeles, CA
90095, USA.
3
California NanoSystems Institute (CNSI),
University of California, Los Angeles, CA 90095, USA.
4
Department of Surg ery, David Geffen School of
Medicine, University of California, Los Angeles, CA 90095, USA.
*These authors contributed equally to this work.
†Corresponding author. Email: ozcan@ucla.edu
Downloaded from https://www.science.org on August 29, 2024
each layer’s neurons were physically encoded
using the relative thickness of each 3D-printed
neuron. Numerical testing of this five-layer D
2
NN
design achieved a classification accuracy of 91.75%
over ~10,000 test images (Fig. 3C). To quantify the
match between these numerical testing results
and our experiments, we 3D-printed 50 hand-
written digits (five different inputs per digit),
selected among the same 91.75% of the test images
for which numerical testing was successful. For
each input object that is uniformly illuminated
with the terahertz source, we imaged the output
plane of the D
2
NN to map the intensity distri-
bution for each detector region that is assigned
to a digit. The results (Fig. 3B) demonstrate the
success of the 3D-printed diffractive neural net-
work and its inference capability: The average
intensity distribution at the output plane of the
network for each input digit clearly reveals that
the 3D-printed D
2
NN was able to focus the input
energy of the beam and achieve a maximum sig-
nal at the corresponding detector region assigned
for that digit. Despite 3D-printing errors, possible
alignment issues, and other experimental error
sources in our setup (14), the match between the
experimental and numerical testing of our five-
layer D
2
NN design was found to be 88% (Fig. 3B).
This relatively small reduction in the perform-
ance of the experimental network compared to
our numerical testing is especially pronounced
for the digit 0 because it is challenging to 3D-
print the large void region at t he center of the
digit. Similar printing challenges were also ob-
served for other digits that have void regions;
e.g.,6,8,and9(Fig.3B).
Next, we tested the classification performance
of D
2
NN framework with a more complicated
image dataset—i.e., the Fashion-MNIST dataset
(19), which includes 10 classes, each representing
a fashion product (t-shirts, trousers, pullovers,
dresses, coats, sandals, shirts, sneakers, bags, and
ankle boots; see fig. S3 for sample images). In gen-
eral, for a coherently illuminated D
2
NN, we can use
the amplitude and/or phase channels of the input
plane to represent data to be classified or processed.
In our digit classification results reported earlier,
input objects were encoded by using the ampli-
tude channel, and to demonstrate the utility of
the phase channel of the network input, we en-
coded each input image corresponding to a fash-
ion product as a phase-only object modulation
(14). Our D
2
NN inference results (as a function of
the number of layers, neurons, and connections)
for classification of fashion products are sum-
marizedinfigs.S4andS5.Toprovideanexample
of our performance, a phase-only and a complex-
valued modulation D
2
NN with N = 5 diffractive
layers (sharing the same physical network dimen-
sions as the digit classification D
2
NN shown
in Fig. 2A) reached an accuracy of 81.13 and
86.33%, respectively (fig. S4). By increasing the
number of diffractive lay ers to N = 1 0 and the
total number of neurons to 0.4 million, our
classification accuracy increased to 86.60% (fig.
S5). For convolutional neural net–based standard
deep learning, the state-of-the-art performance
for Fashion-MNIST classification accuracy has
been reported as 96.7%, using ~8.9 million learn-
able parameters and ~2.5 million neurons (20).
To experimentally demonstrate the perform-
ance of fashion product classification using a
physical D
2
NN, we 3D-printed our phase-only
five-layer design and 50 fashion products used
as test objects (five per class) on the basis of the
same procedures employed for the digit classi-
fication dif fractive network (Fig s. 2A and 3),
except that each input object information was
encoded in the phase channel. Our results are
summarized in Fig . 4, revealing a 90% match
between the experimental and numerical testing
of our five-layer D
2
NN design, with five errors
out of 50 fashion products. Compared with digit
classification (six errors out of 50 digits; Fig. 3),
this experiment yielded a slightly better match
Lin et al., Science 361, 1004–1008 (2018) 7 September 2018 2of5
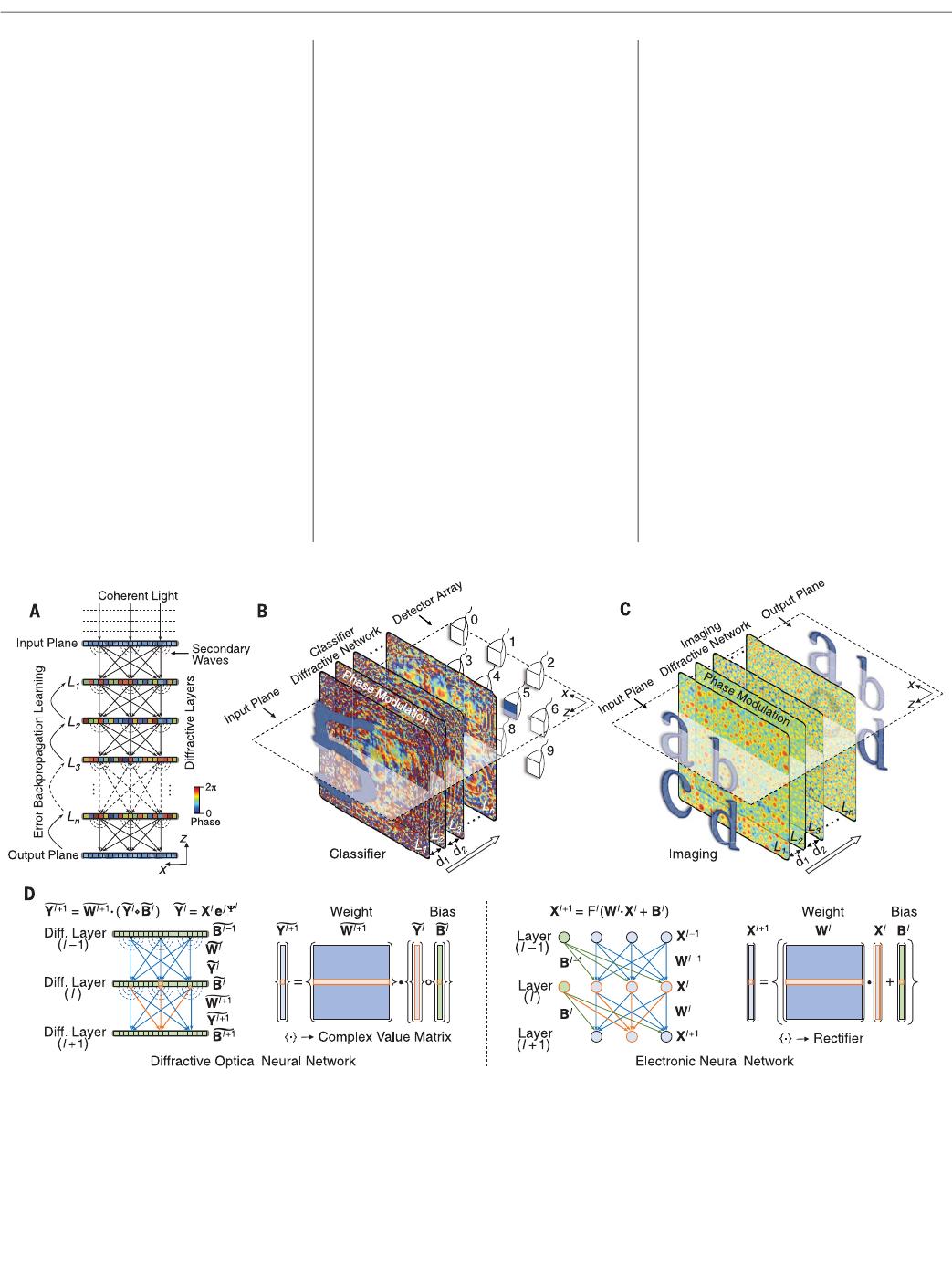
Fig. 1. Diffractive deep neural networks (D
2
NNs). (A)AD
2
NN comprises
multiple transmissiv e (or reflectiv e) layer s, where each point on a given layer acts
as a neuron, with a complex -valu ed transmission (or reflection) coefficient. The
transmis sion or reflection coefficients of each layer can be traine d by using deep
learning to perform a function between the input and output planes of the
network. After this learning phase, the D
2
NN design is fixed; once fabricated or
3D-printed, it performs the learned function at the speed of light. L, layer. (B and
C) We trained and experimen tally implemented different types of D
2
NNs:
(B) classifier (for handwritten digits and fashion pro ducts) and (C) imager .
d,distance.(D) Comparison between a D
2
NN and a convention al neural network
(14). Based on coherent waves, the D
2
NN operates on complex -valued inputs,
with multiplicative bias terms. Wei ghts in a D
2
NN are based on free-space
diffraction and determine the interference of the secondary waves that ar e phase-
and/or amplitude-modulated by the previous layers. “o” denotes a Hadamard
product operation. “Ele ctroni c neural network” ref ers to the convention al neural
netwo rk virtually implemented in a computer. Y, optical field at a given layer;
Y, phase of the optical field; X, amplitude of the optical field; F, nonlinear rectifier
function [see (14) for a discussion of optical nonlinearit y in D
2
NN].
RESEARCH | REPORT
Downloaded from https://www.science.org on August 29, 2024
of 5
免费下载
【版权声明】本文为墨天轮用户原创内容,转载时必须标注文档的来源(墨天轮),文档链接,文档作者等基本信息,否则作者和墨天轮有权追究责任。如果您发现墨天轮中有涉嫌抄袭或者侵权的内容,欢迎发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。
下载排行榜


文档被以下合辑收录
评论