VLDB 2024_LM-SRPQ Efficiently Answering Regular Path Query in Streaming Graphs_gStore.pdf

墨天轮福利君

525

13页

4次

2024-09-05

免费下载

LM-SRPQ: Eiciently Answering Regular Path ery in

Streaming Graphs

Xiangyang Gou

The Chinese University of

Hong Kong

xygou@se.cuhk.edu.hk

Xinyi Ye

Peking University

yexinyi@pku.edu.cn

Lei Zou

Peking University

zoulei@pku.edu.cn

Jerey Xu Yu

The Chinese University of

Hong Kong

yu@se.cuhk.edu.hk

ABSTRACT

Regular path query (RPQ) is a basic operation for graph data anal-

ysis, and persistent RPQ in streaming graphs is a new-emerging

research topic. In this paper, we propose a novel algorithm for

persistent RPQ in streaming graphs, named LM-SRPQ. It solves

persistent RPQ with a combination of intermediate result mate-

rialization and real-time graph traversal. Compared to prior art,

it merges redundant storage and computation, achieving higher

memory and time eciency. We carry out extensive experiments

with both real-world and synthetic streaming graphs to evaluate its

performance. Experiment results conrm its superiority compared

to prior art in both memory and time eciency.

PVLDB Reference Format:

Xiangyang Gou, Xinyi Ye, Lei Zou, and Jerey Xu Yu. LM-SRPQ: Eciently

Answering Regular Path Query in Streaming Graphs. PVLDB, 17(5): 1047 -

1059, 2024.

doi:10.14778/3641204.3641214

PVLDB Artifact Availability:

The source code, data, and/or other artifacts have been made available at

https://github.com/StreamingTriangle/LM-SRPQ.

1 INTRODUCTION

Graph is an omnipresent data form for representation of large-

scale entities and their relationships. It is used in various elds

like biochemistry, social networks and knowledge graphs. Many

graph-based applications require continuous updates and deal with

streaming graphs. A streaming graph is an unbounded sequence

of data items received from data sources. Each data item represents

an edge between two vertices. Together these data items form a

dynamic graph. For example, in Twitter, user communication can

be organized as a streaming graph, where each data item represents

an interaction (edge) between two users (vertex). Up to 12

𝑘

new

edges need to be processed per second in this streaming graph [

Due to the unboundedness of streaming graphs, the entire graph

is not available to analysis algorithms. Additionally, many stream-

ing graph applications focus on real-time analysis, and therefore

focus on more recent data. These issues are usually addressed with

the sliding window model [

]. A sliding window maintains data

∗ Corresponding author is Lei Zou.

This work is licensed under the Creative Commons BY-NC-ND 4.0 International

License. Visit https://creativecommons.org/licenses/by-nc-nd/4.0/ to view a copy of

this license. For any use beyond those covered by this license, obtain permission by

emailing info@vldb.org. Copyright is held by the owner/author(s). Publication rights

licensed to the VLDB Endowment.

Proceedings of the VLDB Endowment, Vol. 17, No. 5 ISSN 2150-8097.

doi:10.14778/3641204.3641214

items in a recent time period, like 12 hours. When the window

moves, older data that falls outside this interval is discarded and

new data replaces it. The sliding window model is widely used in

both research [14, 22, 25] and industrial applications [29].

In streaming graph applications, systems generally deal with

persistent queries that are previously registered and continuously

monitored. The answer set of a persistent query is continuously

maintained and updated in real time as the streaming graph changes.

For example, fraud detection can be specied as a persistent query

continuously monitored for the emergence of certain graph patterns.

Persistent versions of many common graph queries have been

studied, such as subgraph matching [

], cycle detection[

path navigation [25, 26] and triangle counting [14, 31].

In this paper, we focus on persistent Regular Path Query (RPQ

for short) in streaming graphs with a sliding window model. A

regular path query nds vertex pairs connected by a path satisfy-

ing a regular expression in a directed, edge-labeled multi-graph.

RPQ is an important path navigation operation in elds like social

graphs and Semantic Web. It is also supported by many graph query

languages such as SPARQL and Cypher.

RPQ in static graphs has been studied for decades [

However, RPQ research in streaming graphs is in its infancy. Pacaci

et.al. [

] are the rst to dene persistent RPQ over streaming

graphs, and they propose a novel algorithm called RAPQ to solve

this problem. RAPQ transforms RPQ problem into a reachability

problem in a product graph, which is a cartesian product of the

streaming graph and a query graph generated from the regular

expression. Persistent RPQ can be answered by incrementally nd-

ing new paths in this product graph. However, it will be time-

consuming to search new paths from scratch upon each streaming

graph update. RAPQ materializes existing paths to all the succes-

sors of a qualied product graph node with a tree called

tree

. Then it updates

trees and extends existing paths to nd new

paths when the streaming graph is updated. In [

], they further

combine persistent RPQ with persistent graph pattern matching

and propose an algebra for complex queries in streaming graphs.

RAPQ algorithm is also extended in [

], and the new algorithm is

called S-PATH. Timestamps of regular paths are maintained in S-

PATH to enable further analysis. An example of

trees in S-PATH

is shown in Figure 2, which we will discuss in detail in Section 2.2.

S-PATH can eciently process updates in the streaming graph

but at the cost of high memory consumption. According to [

69% of organic RPQs (RPQs issued by browsers) in Wikidata query

In the following sections, we call vertex in the product graph as “node”, in order to

distinguish them from “vertex” in the streaming graph. Besides, the trees built in [

]

are originally called spanning trees, we change their name to avoid confusion with

the spanning tree in graph theory.

1047

log are recursive, namely containing Kleene stars. For these re-

cursive queries,

trees built in S-PATH have no depth constraint

and can be very large. For example, according to our experiments

with StackOverow, a real-world social network dataset, when an-

swering RPQ

𝑎

∗

𝑏

∗

in a sliding window with 180

𝑘

edges and 59

𝑘

vertices, there are 3

𝑘 Δ

trees with size above 21

𝑘

in S-PATH. The

total number of tree nodes is 96

𝑀

, and the memory cost of S-PATH

is more than 600 times larger than the original streaming graph.

In real-world applications, we usually need to monitor multiple

persistent queries at the same time, and the total memory cost will

be multiple times higher. Such high memory consumption limits

the scalability of the algorithm, especially when the application

runs in embedded devices like hubs and routers.

In this paper, we propose landmark-based streaming RPQ (LM-

SRPQ) to decrease the size of the

tree forests while keeping a high

update speed. We notice that there are common subtrees with the

same root in dierent

trees, resulting in redundant storage. The

subtree with root

𝑣

𝑖

in a

tree

𝑇

stores paths from

𝑣

𝑖

to a subset of

its successors, which are fragments of paths from the root of

𝑇

these successors. Common subtrees in dierent

trees are induced

by common path fragments. Therefore, we can decrease memory

usage by merging these common path fragments, which leads to

the merging of common subtrees. We propose to select a group of

nodes as landmarks. Each path in the product graph can be split into

a sequence of local paths, which are path fragments containing

no landmarks. We build a

tree for each landmark

𝑣

𝑖

to maintain

local paths starting from

𝑣

𝑖

. Such a

tree is called a landmark tree,

or LM tree for short. We also build

trees for the original tree roots

in S-PATH, and they maintain local paths starting from these tree

roots. Then we compute paths in the product graph and answer

persistent RPQ by continuously computing concatenations of local

paths. Each local path from a landmark

𝑣

𝑖

to its successor

𝑣

𝑗

may

participate in the computation of multiple product graph paths,

corresponding to common fragments in these paths. In prior art,

this local path will be stored multiple times in the common subtrees

𝑣

𝑖

. But in our method, we only need to store it once in the LM

tree of 𝑣

𝑖

. Therefore, redundant storage is eliminated.

However, there are two major challenges in LM-SRPQ:

First, computing local path concatenations raises a performance

issue. In LM-SRPQ, we build a dependency graph

𝐺

𝑑

to aid us in

the local path concatenation. Each node in

𝐺

𝑑

represents a

tree

and each edge represents the local path connecting the roots of

two

trees. Concatenated local path sequences can be represented

as paths in

𝐺

𝑑

. When a new tuple arrives in the streaming graph,

we rst update the Δ trees, producing new local paths and adding

new edges in

𝐺

𝑑

. Then we need to traverse in

𝐺

𝑑

to nd new

paths containing the new edge, which represents new local path

sequences. The cost of such traversal is high and may slow down

the entire algorithm. We need additional acceleration techniques.

Second, how to select a proper landmark set raises another chal-

lenge. Dierent landmark sets result in dierent

tree forest sizes.

Moreover, as discussed above, the dependency graph traversal is the

bottleneck of the algorithm, and the landmark number inuences

the number of LM trees, as well as the dependency graph size. We

need to bound the landmark number to control the dependency

graph traversal cost. Therefore, we hope to select a landmark set

with a bounded size and try to minimize the

tree forest size. The

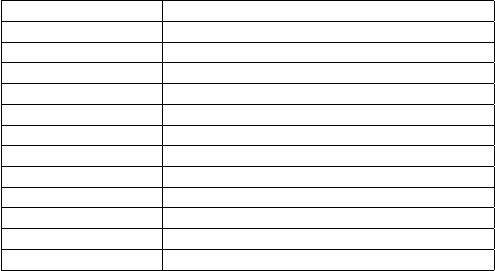
Table 1: Notation Table

Notation Meaning

𝑊 Sliding window

𝛽 Sliding interval

𝐺

𝜏

Snapshot graph at time 𝜏

𝑒.𝑡𝑠 / 𝑝.𝑡𝑠 Timestamp of edge 𝑒 / path 𝑝

𝜙 (𝑒 ) / 𝜙 (𝑝 ) Label of edge 𝑒 / path 𝑝

𝐴

𝑅

DFA built for regular expression 𝑅

𝐴

𝑅

.𝐹 Final state set in 𝐴

𝑅

𝑠

/ 𝑠

𝑓

Initial state / nal state in DFA

𝑃 (𝐺, 𝐴) Product graph of graph 𝐺 and DFA 𝐴

⟨𝑣

𝑖

, 𝑠

𝑖

⟩ Product graph node with vertex 𝑣

𝑖

and state 𝑠

𝑖

𝑇

𝑣

𝑖

,𝑠

𝑖

Δ tree with root node ⟨𝑣

𝑖

, 𝑠

𝑖

⟩.

𝑇

𝑣

𝑖

,𝑠

𝑖

.⟨𝑣

𝑗

, 𝑠

𝑗

⟩.𝑡𝑠 Timestamp of node ⟨𝑣

𝑗

, 𝑠

𝑗

⟩ in tree 𝑇

𝑣

𝑖

,𝑠

𝑖

search space of such landmark selection is exponential, making it

computationally impossible to nd an optimal solution. We have

to resort to a greedy algorithm. Besides, we need to continuously

update the landmark set to keep up with the streaming graph.

In LM-SRPQ, we use a greedy algorithm in landmark selection,

which tries to minimize the size of the

tree forest while bounding

the number of

trees. Besides, we also continuously maintain an

additional index called TI-map in each LM tree, which records the

timestamps of paths starting from the tree root. Based on these

timestamps we propose a set of rules for pruning in dependency

graph traversal. We carry out extensive experiments in two real-

world datasets and one synthetic dataset to evaluate the perfor-

mance of our algorithm. The result shows that LM-SRPQ reduces

the memory usage of prior art S-PATH by at most 30 times. More-

over, as common subtree merging reduces the

tree update cost

and ecient pruning reduces the dependency graph traversal cost,

LM-SRPQ is at most 4.5 times faster than S-PATH.

In summary, we made the following contributions in this paper:

(1)

We propose a novel algorithm for persistent RPQ in stream-

ing graphs, named LM-SRPQ. It decreases the memory cost

as well as the update cost of the prior art by eliminating

redundant storage and computation.

(2)

To balance the time and memory cost of our algorithm, we

propose a greedy landmark selection algorithm to balance

the number of

trees and the size of the

tree forest, as

well as an additional index that helps to prune the recursive

traversal in the dependency graph.

(3)

We carry out extensive experiments to evaluate our algo-

rithm, which conrms its superiority against prior art.

2 PRELIMINARIES

We formally dene our problem in Section 2.1 and list frequently-

used notations in Table 1. To better understand the motivation of

our method, we briey introduce S-PATH [

] in Section 2.2, which

is the prior art for RPQ over streaming graphs in the literature.

2.1 Problem Denition

Definition 2.1. Graph. A directed, edge-labeled graph is dened

𝐺 = (𝑉, 𝐸, Σ, 𝜙)

, where

𝑉

is a vertex set,

𝐸 ⊂ 𝑉 × 𝑉

is an edge set,

Σ is a set of labels, and 𝜙 : 𝐸 → Σ is an edge labeling function.

1048

of 13

免费下载

文档被以下合辑收录

VLDB2024 数据库顶会论文（共31篇）

本合辑收录了VLDB2024 数据库顶会论文。

关注

文档被以下合辑收录

评论