REGER: Reordering Time Series Data for Regression Encoding.pdf

Apache IoTDB

158

13页

0次

2024-09-24

100墨值下载

REGER: Reordering Time Series Data for

Regression Encoding

Jinzhao Xiao

Tsinghua University

xjc22@mails.tsinghua.edu.cn

Wendi He

Tsinghua University

he-wd21@mails.tsinghua.edu.cn

Shaoxu Song

∗

BNRist, Tsinghua University

sxsong@tsinghua.edu.cn

Xiangdong Huang

Timecho Ltd

hxd@timecho.com

Chen Wang

Timecho Ltd

wangchen@timecho.com

Jianmin Wang

Tsinghua University

jimwang@tsinghua.edu.cn

Abstract—Regression models are employed in lossless compres-

sion of time series data, by storing the residual of each point,

known as regression encoding. Owing to value ﬂuctuation, the

regression residuals could be large and thus occupy huge space.

It is worth noting that compared to the ﬂuctuating values, time

intervals are often regular and easy to compress, especially in

the IoT scenarios where sensor data are collected in a preset

frequency. In this sense, there is a trade-off between storing

the regular timestamps and ﬂuctuating values. Intuitively, rather

than in time order, we may exchange the data points in the

series such that the nearby ones have both smoother timestamps

and values, leading to lower residuals. In this paper, we propose

to reorder the time series data for better regression encoding.

Rather than recomputing from scratch, efﬁcient updates of

residuals after moving some points are devised. The experimental

comparison over various real-world datasets, either public or

collected by our industrial partners, illus trates the superiority of

the proposal in compression ratio. The method, REGression En-

coding with Reordering (REGER), has now become an encoding

method in an open-source time series database, Apache IoTDB.

Index Terms—time series, regression, encoding, reordering

I. INTRODUCTION

While a number of data encoding methods can be applied

to compress time series [36], lossless regression encoding is

found effective, such as FIRE in SPRINTZ [11]. The idea is

to learn regression models over the time series and record the

corresponding residuals. By adding model predictions with the

stored residuals, it decodes the compressed time series.

To illustrate the signiﬁcance of regression encoding, con-

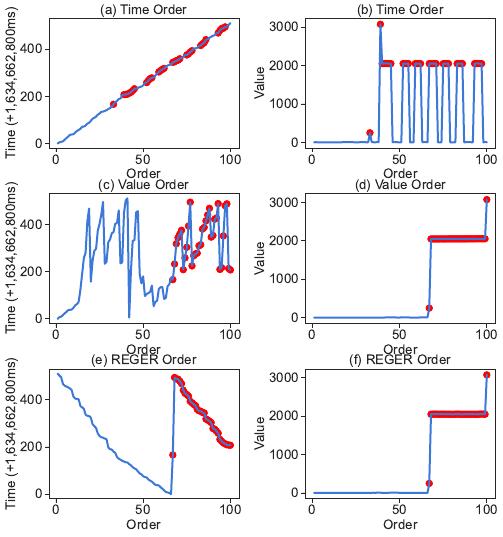
sider the sequence of timestamps in Figure 1(a). As shown, the

timestamps have a clear increasing pattern and thus are highly

predictable by a regression model. The corresponding residuals

of the auto-regression model are small as reported in Figure

2(a). Storing the much smaller residuals and regression ratio is

obviously more efﬁcient than the original timestamps. Hence,

the application scenarios of regression encoding are those

sequences highly predictable with small r egression residuals.

A. Motivation

Unfortunately, time series may have large value ﬂuctuations,

leading to huge space of residuals. For instance, Figure 1(b)

∗

Shaoxu Song (https://sxsong.github.io/) is the corresponding author.

Fig. 1: Data points of timestamps and values cropped from a real-word time

series CS-Sensors in Figure 9(f), ordered by time in (a) and (b ), by value in

red points denote those moved by our REGER.

illustrates the values of points ordered by timestamps. It is

difﬁcult to learn a regression model to capture the ﬂuctuating

pattern. Hence, the model prediction will be inaccurate, and

the residuals are l arge to store for lossless regression encoding.

Note that data points in a time series may not always

be sorted by timestamps [37]. For example, one may order

a series by values [35]. While the values become smoother

and better for regression as illustrated in Figure 1(d), the

corresponding timestamps in Figure 1(c) ﬂuctuate more sig-

niﬁcantly than that ordered by time in Figure 1(a). The overall

residuals of time and value are not improved.

Intuitively, we may only move together some of the data

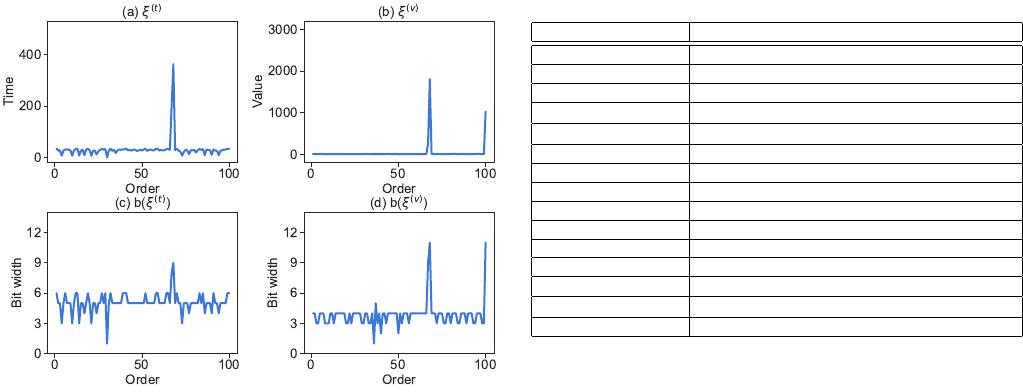
Fig. 2: The encoded series ξ of regression residuals and the corresponding

bitwidth series b(ξ) in Example 1, for time series x in Figure 1(a) and (b)

points with both similar time and value in the series. For

example, we exchange the red points to the new positions

such that the signiﬁcantly ﬂuctuating values originally in

Figure 1(b) become more stable for regression in Figure 1(f).

Meanwhile, the corresponding nearby timestamps in Figure

1(e) are similar as well. As shown, the newly introduced

timestamp ﬂuctuation is not as signiﬁcant as that removed in

value. It is also less ﬂuctuating than Figure 1(c), where the

points are ordered by value. In this sense, the overall residuals

of time and value are reduced in regression encoding.

B. Solution

Note that timestamps are crucial in IoT applications. Hence,

in regression encoding, both timestamps and values are en-

coded and stored, in the same order of data points. For data

points ordered by timestamps in Figure 1(a)(b), while the

timestamp storage is effective, the corresponding values have

large ﬂuctuations and thus large auto-regression residuals. On

the other hand, for data points ordered by values in Figure

1(c)(d), the value storage is efﬁcient, whereas the correspond-

ing timestamps suffer large ﬂuctuations and again large auto-

regression residuals. To balance the trade-off, we propose to

ﬁnd a better ordering of data points (by Algorithm 1) that may

have smaller residuals of auto-regression on timestamps and

values, respectively, and consequently the total storage usage.

Since both timestamps and values are encoded and stored,

they can be naturally decoded, respectively, by adding the

auto-regression model predictions with the stored residuals.

The decoded data points of timestamps and values are then

ordered again on timestamps, recovering exactly the original

time series by Algorithm 2. Therefore, REGER is lossless and

will not destroy the downstream tasks.

C. Contribution

Our major contributions in this study are as follows.

TABLE I: Notations

Notation Description

x a time series

n the number of values in a block of time series

q the number of values in a pack of time series

(t)

, x

(v)

timestamps and values of time series x

(t)

, f

(v)

regression models for timestamp and value

ǫ residual series of x

ξ encoded series o f ǫ

b(ξ) bitwidth series of ξ

x reordered by order A

α→β

reorder x by moving α-th point to position β

g(j ) points affected by moving a point from α

h(j ) points affected by moving a point to j

H (ξ

g(j )

),H (ξ

h(j )

) residual cost of g(j ) and h(j ) points in ξ

H (ξ

[1,n]\g(j )\h(j )

) residual cost of unchanged points in ξ

p the order of the autoregressive model

(1) We formalize the problem of time series reordering

for regression encoding, in Section II. Finding the optimal

reordering of time series for regression encoding, however,

is costly and not affordable during the extremely fast data

ingestion, especially in t he IoT scenarios.

(2) We propose an efﬁcient heuristic algorithm that moves

one point at a time, leading to lower residuals, in Section III.

Rather than recomputing from scratch, an efﬁcient incremental

strategy is devised for updating residuals after point moving.

(3) Remarkably, the proposed method, REGression Encod-

ing with Reordering (REGER), has now become an encoding

method in an open-source time series database, Apache IoTDB

[18], [34]. We present the system deployment in Section IV.

(4) We conduct extensive experiments over various real-

world datasets. The results demonstrate that the reordered time

series has better compression ratio than the natural time order.

The code of REGER method has been included in the

system repository of Apache IoTDB [6]. The experiment

related code and data are available in [7] for reproducibility.

Table I lists the frequently used notations.

II. ENCODING METHOD

Since large ﬂuctuations like abnormal behaviors often ap-

pear in t ime series, the residuals will be very l arge for regres-

sion encoding. It leads to more bit widths for storing residuals,

higher space cost. Thus, we propose a method that reorders

the time series, which could reduce the bit widths of residuals.

In the following, we introduce regression encoding in Section

II-B and time s eries reordering problem in Section II-C.

A. Preliminary

Consider a time series of n data points. It usually corre-

sponds to a block in the database management system for data

encoding, as introduced in Section IV below.

Deﬁnition 1 (Time Series): A time series is denoted by two

sequences of time and value,

x = (x

(t)

, x

(v)

where x

(t)

contains n timestamps, and x

(v)

has n values.

(t)

= (x

(t)

, x

(t)

, . . . , x

(t)

), x

(v)

= (x

(v)

, x

(v)

, . . . , x

(v)

of 13

100墨值下载

关注

评论