




CCS 2024. Almost Instance-optimal Clipping for Summation Problems in the Shuffle Model of Differential Privacy_OceanBase.pdf
免费下载

Almost Instance-optimal Clipping for Summation Problems in the
Shule Model of Dierential Privacy
Wei Dong
Nanyang Technological University
Singapore, Singapore
wei_dong@ntu.edu.sg
Qiyao Luo
OceanBase, Ant Group
Shanghai, China
luoqiyao.lqy@antgroup.com
Giulia Fanti
Carnegie Mellon University
Pittsburgh, United States
gfanti@andrew.cmu.edu
Elaine Shi
Carnegie Mellon University
Pittsburgh, United States
runting@gmail.com
Ke Yi
Hong Kong University of Science and
Technology
Hong Kong, Hong Kong
yike@cse.ust.hk
Abstract
Dierentially private mechanisms achieving worst-case optimal
error bounds (e.g., the classical Laplace mechanism) are well-studied
in the literature. However, when typical data are far from the worst
case, instance-specic error bounds—which depend on the largest
value in the dataset—are more meaningful. For example, consider
the sum estimation problem, where each user has an integer
𝑥
𝑖
from the domain
{
0
,
1
, . . . ,𝑈 }
and we wish to estimate
Í
𝑖
𝑥
𝑖
. This
has a worst-case optimal error of
𝑂 (𝑈 /𝜀)
, while recent work has
shown that the clipping mechanism can achieve an instance-optimal
error of
𝑂 (max
𝑖
𝑥
𝑖
· log log𝑈 /𝜀)
. Under the shue model, known
instance-optimal protocols are less communication-ecient. The
clipping mechanism also works in the shue model, but requires
two rounds: Round one nds the clipping threshold, and round
two does the clipping and computes the noisy sum of the clipped
data. In this paper, we show how these two seemingly sequential
steps can be done simultaneously in one round using just 1
+𝑜 (
1
)
messages per user, while maintaining the instance-optimal error
bound. We also extend our technique to the high-dimensional sum
estimation problem and sparse vector aggregation (a.k.a. frequency
estimation under user-level dierential privacy).
CCS Concepts
• Security and privacy → Privacy-preserving protocols.
Keywords
Dierential privacy; sum estimation
ACM Reference Format:
Wei Dong, Qiyao Luo, Giulia Fanti, Elaine Shi, and Ke Yi. 2024. Almost
Instance-optimal Clipping for Summation Problems in the Shue Model of
Dierential Privacy. In Proceedings of the 2024 ACM SIGSAC Conference on
Computer and Communications Security (CCS ’24), October 14–18, 2024, Salt
Lake City, UT, USA. ACM, New York, NY, USA, 15 pages. https://doi.org/10.
1145/3658644.3690225
This work is licensed under a Creative Commons Attribution
International 4.0 License.
CCS ’24, October 14–18, 2024, Salt Lake City, UT, USA
© 2024 Copyright held by the owner/author(s).
ACM ISBN 979-8-4007-0636-3/24/10
https://doi.org/10.1145/3658644.3690225
1 Introduction
The shue model [
10
,
12
,
20
] of dierential privacy (DP) is widely-
studied in the context of DP computation over distributed data.
The model has 3 steps: (1) Each client uses a randomizer
R(·)
to
privatize their data. (2) A trusted shuer randomly permutes the
inputs from each client and passes them to an untrusted analyzer,
which (3) conducts further analysis. Unlike the central model of DP,
where a trusted curator has access to all the data, the shue model
provides stronger privacy protection by removing the dependency
on a trusted curator. Unlike the local model, where clients send
noisy results to the analyzer directly, the addition of the trusted
shuer allows for a signicantly improved privacy-accuracy trade-
o. For problems like bit counting, shue-DP achieves an error of
𝑂 (
1
/𝜀)
with constant probability
1
[
23
], matching the best error of
central-DP, while the smallest error achievable under local-DP is
𝑂 (
√
𝑛/𝜀) [11, 13].
The summation problem, a fundamental problem with applica-
tions in statistics [
9
,
27
,
33
], data analytics [
15
,
44
], and machine
learning such as the training of deep learning models [
1
,
2
,
8
,
41
]
and clustering algorithms [
42
,
43
], has been studied in many works
under the shue model [
6
,
7
,
12
,
24
–
26
]. In this problem, each
user
𝑖 ∈ [𝑛]
:
= {
1
, . . . , 𝑛}
holds an integer
𝑥
𝑖
∈ {
0
,
1
, . . . ,𝑈 }
and
the goal is to estimate
Sum(𝐷)
:
=
Í
𝑖
𝑥
𝑖
, where
𝐷 = (𝑥
1
, . . . , 𝑥
𝑛
)
.
All of these works for sum estimation under shue-DP focus on
achieving an error of
𝑂 (𝑈 /𝜀)
. Such an error can be easily achieved
under central-DP, where the curator releases the true sum after
masking it with a Laplace noise of scale
𝑈 /𝜀
. In the shue-DP
model, besides error, another criterion that should be considered
is the communication cost. The recent shue-DP summation pro-
tocol of [
24
] both matches the error of central-DP and achieves
optimal communication. More precisely, it achieves an error that is
just 1
+𝑜 (
1
)
times that of the Laplace mechanism, while each user
just sends in expectation 1
+𝑜 (
1
)
messages, each of a logarithmic
number of bits.
However, in real applications (as well as in [24]), 𝑈 must be set
independently of the dataset; to account for all possible datasets,
it should be conservatively large. For instance, if we only know
that the
𝑥
𝑖
’s are 32-bit integers, then
𝑈 =
2
32
−
1. Then the error
1
In Section 1, all stated error guarantees hold with constant probability. We will make
the dependency on the failure probability 𝛽 more explicit in later sections.
BBAAD9C20180234D78A0072836F0B6D0E2B9B2091CC78BA0ADD98334B1332B246B4CB438915CAB0D22592008984631EBB0E921BAC1D09B911BBFC23670BE3FD6241144ADDF2589F764B7292767674B426EF7E18E714D1414D8BA819CE1F6ACC8D7E62996BE3
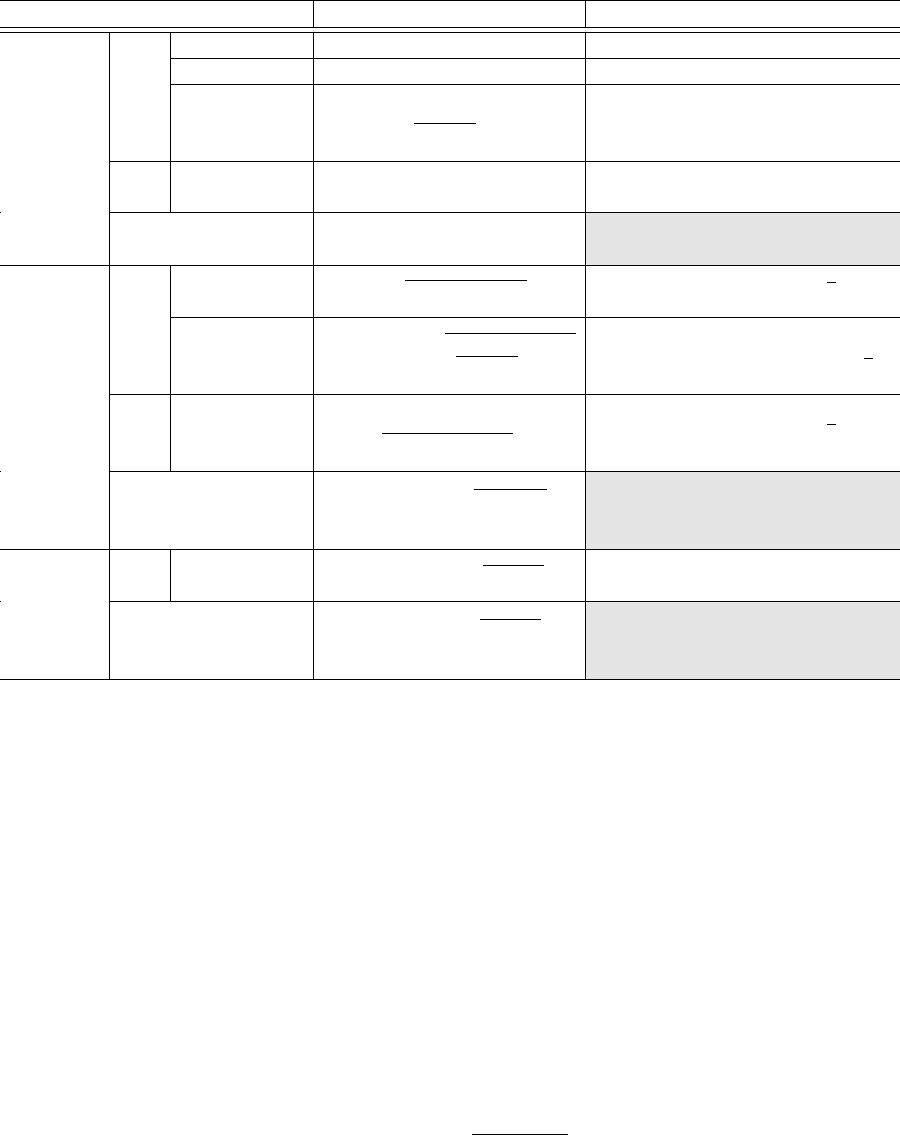
CCS ’24, October 14–18, 2024, Salt Lake City, UT, USA Wei Dong, Qiyao Luo, Giulia Fanti, Elaine Shi, and Ke Yi
Mechanism Error Average messages sent by each user
1-D
Sum
Prior
work
[24] 𝑂
𝑈 /𝜀
1 +𝑜 (1)
[7] 𝑂
𝑈 /𝜀
𝑂 (1)
[27] + [24] + [22]
˜
𝑂
Max(𝐷) · log
3.5
𝑈
log(1/𝛿)/𝜀
Round 1:
˜
𝑂
log
6
𝑈 · log
1/𝛿
/𝜀
Round 2: 1 +𝑜 (1)
Our
result
Theorem
𝑂
Max(𝐷) · log log𝑈 /𝜀
1 +𝑜 (1)
5.1
Best result under
𝑂
Max(𝐷) · log log𝑈 /𝜀
central model [18]
𝑑-D
Sum
Prior
work
[27]
˜
𝑂
𝑈
ℓ
2
𝑑 log(𝑛) log(1/𝛿)/𝜀
𝑑 +
˜
𝑂 (𝑑
1.5
log
1.5
(1/𝛿)/(𝜀
√
𝑛)
[27] + [24] +[22]
˜
𝑂
Max
ℓ
2
(𝐷) ·
𝑑 log(𝑛𝑑) log(1/𝛿)
+log
3.5
𝑈
ℓ
2
·
log(1/𝛿)
/𝜀
Round 1:
˜
𝑂
log
6
𝑈
ℓ
2
· log(1/𝛿)/𝜀
Round 2: 𝑑 +
˜
𝑂 (𝑑
1.5
log
1.5
(1/𝛿)/(𝜀
√
𝑛)
Our
result
Theorem
6.2
𝑂
Max
ℓ
2
(𝐷) · log(𝑑 log𝑈
ℓ
2
)
·
𝑑 log(𝑛𝑑) log(1/𝛿)/𝜀
𝑑 +
˜
𝑂 (𝑑
1.5
log
1.5
(1/𝛿)/(𝜀
√
𝑛)
Best result under
central model [17]
𝑂
Max
ℓ
2
(𝐷) ·
𝑑 log(1/𝛿)
+log log𝑈
ℓ
2
/𝜀
Sparse
Vector
Aggregation
Our
result
Theorem
˜
𝑂 (Max
ℓ
2
(𝐷) · log 𝑑
log(1/𝛿)/𝜀)
∥𝑥
𝑖
∥
1
+ 1 +𝑂 (𝑑
1.5
log𝑑 log
1.5
(1/𝛿)/(𝜀𝑛))
7.1
Best result under
central model [17]
𝑂
Max
ℓ
2
(𝐷) ·
log(1/𝛿)
+log log𝑈
ℓ
2
/𝜀
Table 1: Comparison between our results and prior works on sum estimation, high-dimensional sum estimation, and sparse
vector aggregation under shule model, where we use the absolute error,
ℓ
2
error, and
ℓ
∞
error as the error metrics. Each
message contains
𝑂 (log𝑈 + log 𝑑 + log 𝑛)
bits. The mechanism without an indicator for the round runs in a single round. Our
communication cost for 1-D Sum requires the condition 𝑛 = 𝜔 (log
2
𝑈 ).
of
𝑂 (𝑈 /𝜀)
could dwarf the true sum for most datasets. Notice that
sometimes some prior knowledge is available, and then a smaller
𝑈
could be used. For example, if we know that the
𝑥
𝑖
’s are people’s
incomes, then we may set
𝑈
as that of the richest person in the
world. Such a
𝑈
is still too large for most datasets as such a rich
person seldom appears in most datasets.
Instance-Awareness. The earlier error bound of
𝑂 (𝑈 /𝜀)
can
be shown to be optimal, but only in the worst case. When typical
input data are much smaller than
𝑈
, an instance-specic mechanism
(and error bound) can be obtained—i.e., a mechanism whose error
depends on the largest element of the dataset. In the example of
incomes above, an instance-aware mechanism would achieve an
error proportional to the actual maximum income in the dataset.
This insight has recently been explored under the central model of
DP [4, 15, 21, 27, 36, 39].
A widely used technique for achieving instance-specic error
bounds under central-DP is the clipping mechanism [
4
,
27
,
36
,
39
].
For some
𝜏
, each
𝑥
𝑖
is clipped to
Clip(𝑥
𝑖
, 𝜏)
:
= min(𝑥
𝑖
, 𝜏)
. Then we
compute the sum of
Clip(𝐷,𝜏)
:
=
Clip(𝑥
𝑖
, 𝜏) | 𝑖 =
1
, . . . , 𝑛
and add
a Laplace noise of scale
𝑂 (𝜏/𝜀)
. Note that the clipping introduces
a (negative) bias of magnitude up to
Max(𝐷) · |{𝑖 ∈ [𝑛] | 𝑥
𝑖
> 𝜏 }|
,
where
Max(𝐷)
:
= max
𝑖
𝑥
𝑖
. Thus, one should choose a good clipping
threshold
𝜏
that balances the DP noise and bias. Importantly, this
must be done in a DP fashion, and this is where all past investiga-
tions on the clipping mechanism have been devoted. In the central
model, the best error bound achievable is
𝑂
Max(𝐷) · log log𝑈 /𝜀
[
18
].
2
For the real summation problem, such an error bound is con-
sidered (nearly) instance-optimal, since any DP mechanism has to
incur an error of
Ω(Max(𝐷))
on either
𝐷
or
𝐷 − {Max(𝐷)}
[
45
].
The factor of
log log𝑈 /𝜀
is known as the “optimality ratio”. It has
been shown that the optimality ratio
𝑂 (log log𝑈 /𝜀)
is the best pos-
sible in the case of
𝛿 =
0 (
𝛿
is a privacy parameter, see Section 3.1
2
[
18
] achieves an error of
𝑂 (Max(𝐷 ) log log(Max(𝐷 )))
rather than the cited
𝑂 (Max(𝐷 ) log log𝑈 ))
. The
log log(Max(𝐷 ))
result is more meaningful for the
unbounded domain setting where
𝑈 = ∞
, but in the shue-DP model, there is cur-
rently no known method can handle the unbounded domain case for any problem,
including sum estimation. Our proposed mechanism also only supports the bounded
domain case. Therefore, for simplicity, we ignored this minor dierence and just cited
the log log𝑈 result.
BBAAD9C20180234D78A0072836F0B6D0E2B9B2091CC78BA0ADD98334B1332B246B4CB438915CAB0D22592008984631EBB0E921BAC1D09B911BBFC23670BE3FD6241144ADDF2589F764B7292767674B426EF7E18E714D1414D8BA819CE1F6ACC8D7E62996BE3
of 15
免费下载
【版权声明】本文为墨天轮用户原创内容,转载时必须标注文档的来源(墨天轮),文档链接,文档作者等基本信息,否则作者和墨天轮有权追究责任。如果您发现墨天轮中有涉嫌抄袭或者侵权的内容,欢迎发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。
下载排行榜


评论