




SIGMOD 2024_F3KM_Federated, Fair, and Fast k-means_OceanBase.pdf
免费下载

241
F
3
KM: Federated, Fair, and Fast 𝑘-means
SHENGKUN ZHU, School of Computer Science, Wuhan University, China
QUANQING XU, OceanBase, Ant Group, China
JINSHAN ZENG, School of Computer and Information Engineering, Jiangxi Normal University, China
SHENG WANG
∗
, School of Computer Science, Wuhan University, China
YUAN SUN, La Trobe Business School, La Trobe University, Australia
ZHIFENG YANG, OceanBase, Ant Group, China
CHUANHUI YANG, OceanBase, Ant Group, China
ZHIYONG PENG, School of Computer Science & Big Data Institute, Wuhan University, China
This paper proposes a federated, fair, and fast
𝑘
-means algorithm (F
3
KM) to solve the fair clustering problem
eciently in scenarios where data cannot be shared among dierent parties. The proposed algorithm decom-
poses the fair
𝑘
-means problem into multiple subproblems and assigns each subproblem to a client for local
computation. Our algorithm allows each client to possess multiple sensitive attributes (or have no sensitive
attributes). We propose an in-processing method that employs the alternating direction method of multipliers
(ADMM) to solve each subproblem. During the procedure of solving subproblems, only the computation results
are exchanged between the server and the clients, without exchanging the raw data. Our theoretical analysis
shows that F
3
KM is ecient in terms of both communication and computation complexities. Specically,
it achieves a better trade-o between utility and communication complexity, and reduces the computation
complexity to linear with respect to the dataset size. Our experiments show that F
3
KM achieves a better
trade-o between utility and fairness than other methods. Moreover, F
3
KM is able to cluster ve million
points in one hour, highlighting its impressive eciency.
CCS Concepts: • Computing methodologies → Cluster analysis.
Additional Key Words and Phrases: Federated, Fair, Fast, 𝑘-means, ADMM
ACM Reference Format:
Shengkun Zhu, Quanqing Xu, Jinshan Zeng, Sheng Wang, Yuan Sun, Zhifeng Yang, Chuanhui Yang, and Zhiy-
ong Peng. 2023. F
3
KM: Federated, Fair, and Fast
𝑘
-means. Proc. ACM Manag. Data 1, 4 (SIGMOD), Article 241
(December 2023), 25 pages. https://doi.org/10.1145/3626728
1 INTRODUCTION
The rise of big data has emphasized the crucial role of clustering analysis in data science. This
statistical technique facilitates the exploration of a dataset’s internal structure by organizing data
∗
Corresponding author
Authors’ addresses: Shengkun Zhu, whuzsk66@whu.edu.cn, School of Computer Science, Wuhan University, China;
Quanqing Xu, OceanBase, Ant Group, China, xuquanqing.xqq@oceanbase.com; Jinshan Zeng, School of Computer and
Information Engineering, Jiangxi Normal University, China, jinshanzeng@jxnu.edu.cn; Sheng Wang, School of Computer
Science, Wuhan University, China, swangcs@whu.edu.cn; Yuan Sun, La Trobe Business School, La Trobe University,
Australia, yuan.sun@latrobe.edu.au; Zhifeng Yang, OceanBase, Ant Group, China, zhuweng.yzf@oceanbase.com; Chuanhui
Yang, OceanBase, Ant Group, China, rizhao.ych@oceanbase.com; Zhiyong Peng, School of Computer Science & Big Data
Institute, Wuhan University, China, peng@whu.edu.cn.
Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee
provided that copies are not made or distributed for prot or commercial advantage and that copies bear this notice and the
full citation on the rst page. Copyrights for components of this work owned by others than the author(s) must be honored.
Abstracting with credit is permitted. To copy otherwise, or republish, to post on servers or to redistribute to lists, requires
prior specic permission and/or a fee. Request permissions from permissions@acm.org.
© 2023 Copyright held by the owner/author(s). Publication rights licensed to ACM.
2836-6573/2023/12-ART241 $15.00
https://doi.org/10.1145/3626728
Proc. ACM Manag. Data, Vol. 1, No. 4 (SIGMOD), Article 241. Publication date: December 2023.
BBAAD9C20180234D78A0072836F0B91042B9B20910300BA0A6D98A34B1CB2BF4AB46B438915CAB0722492008984625EBF2E9210AC1D01B511BBFC26E770E3FD824112BAD3C22B9F764942AC767674B912927EA8A7DFF741658BA519C5A64DCC8DEE6249A9E3
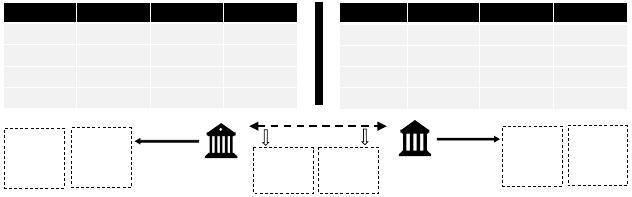
241:2 Shengkun Zhu et al.
Marital Loan Deposit
Divorced 10K 10K
Married 45K 10K
Single 15K 10K
Married 25K 10K
User ID Sex Race Income
1 Male White 50K
2 Male White 40K
3 Female Black 10K
4 Female Asian 45K
User ID
1
2
3
4
Institution B
Institution A
High risk
User 3
User 4
Low risk
User 1
User 2
High risk
User 2
User 4
Low risk
User 1
User 3
High risk
User 2
User 3
Low risk
User 1
User 4
Clustering
Clustering
Data sharing
Fair clustering
Fig. 1. When data sharing is prohibited and fairness is disregarded, institutions A and B obtain inaccurate
and biased results. However, enabling data sharing and implementing fair clustering can lead to accurate and
unbiased results.
points into clusters [
5
]. As one of the most classical clustering algorithms,
𝑘
-means aims to partition
data points into
𝑘
clusters such that the points within a cluster are as close as possible [
49
].
𝑘
-means
has found extensive applications in various domains, including healthcare [
26
,
32
,
42
,
45
], nance
[
14
,
20
,
37
,
55
], education [
29
,
43
], etc. Its usage has facilitated data understanding, improved
decision-making eciency, and provided high-quality services.
However, applying
𝑘
-means in these domains may pose some issues due to legal mandates
[
21
,
28
]. Let us consider the following scenario in Figure 1: two nancial institutions, A and B,
seek to conduct collaborative
𝑘
-means clustering analysis on a set of customers by using the credit
card transaction data to identify distinct credit risk analysis. Due to the sensitivity of nancial
data, such as income and transaction records, each institution is restricted to accessing its own
portion of customer transaction data solely, thereby preventing the direct sharing of raw data.
Furthermore, both institutions aim to ensure that the clustering results adhere to the principle of
fairness, whereby the proportion of protected groups, comprising demographics such as gender and
race, is approximately equal across clusters [
15
]. However, due to data unavailability for sharing
and insucient attention to fairness, institutions A and B cluster the same users but obtain dierent
results with unfairness. Specically, institution A clusters low-income black and Asian females
together, while institution B clusters individuals who are married with high loans. If nancial
institutions are able to obtain additional user features while ensuring fairness, they can improve
the accuracy of credit risk assessment and enhance customer satisfaction [6, 33].
Vertical federated learning (VFL) is a promising framework for addressing the issue of non-
sharable data. It is a distributed machine learning approach that divides features among clients so
that each client possesses an independent set of features while sharing the same set of users [
23
,
34
,
35
,
39
,
51
,
52
]. VFL enables the training and updating of models using data from multiple clients
without exposing raw data. However, current VFL frameworks for clustering face communication
bottlenecks [
31
]. Specically, the communication complexity of existing frameworks is highly
contingent on the dataset size. Ding et al
. [19]
developed a constant approximation scheme for
𝑘
-means clustering, which exhibit linear communication complexity with respect to the dataset size.
Huang et al
. [31]
proposed a technique for reducing communication complexity by constructing
a coreset, which results in sublinear complexity with respect to the dataset size. However, such
communication complexity remains intolerable in the era of big data.
Fairness in federated
𝑘
-means is also a focal point of our concern. Specically, we are concerned
with group fairness, which is a notion that emerged from the disparate impact doctrine [
22
] and
was initially introduced by Chierichetti et al
. [15]
. In the context of clustering, group fairness
can be characterized by the proportional representation of protected groups in each cluster. More
Proc. ACM Manag. Data, Vol. 1, No. 4 (SIGMOD), Article 241. Publication date: December 2023.
BBAAD9C20180234D78A0072836F0B91042B9B20910300BA0A6D98A34B1CB2BF4AB46B438915CAB0722492008984625EBF2E9210AC1D01B511BBFC26E770E3FD824112BAD3C22B9F764942AC767674B912927EA8A7DFF741658BA519C5A64DCC8DEE6249A9E3
of 25
免费下载
【版权声明】本文为墨天轮用户原创内容,转载时必须标注文档的来源(墨天轮),文档链接,文档作者等基本信息,否则作者和墨天轮有权追究责任。如果您发现墨天轮中有涉嫌抄袭或者侵权的内容,欢迎发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。
下载排行榜


评论