IDCE2024-qos Personalized PageRanks over Dynamic Graphs– The Case for Optimizing Quality of Service.pdf

迹部景吾

19页

0次

2025-04-22

免费下载

Personalized PageRanks over Dynamic Graphs

– The Case for Optimizing Quality of Service

Zulun Zhu

Nanyang Technological University

ZULUN001@e.ntu.edu.sg

Sibo Wang

The Chinese University of Hong Kong

swang@se.cuhk.edu.hk

Siqiang Luo

Nanyang Technological University

siqiang.luo@ntu.edu.sg

Dingheng Mo

Nanyang Technological University

dingheng001@e.ntu.edu.sg

Wenqing Lin

Tencent

edwlin@tencent.com

Chunbo Li

Nanyang Technological University

chunbo001@e.ntu.edu.sg

Abstract—We study the problem of Quality-of-Service (QoS)-

Aware Personalized PageRank (PPR) computation. Existing stud-

ies mostly focus on improving the PPR query processing time.

However, the query processing time alone may not reﬂect the ser-

vice quality in real-world PPR-based systems. The query response

time can be a more service-relevant measure in many applications

such as the online game service of Tencent and the related-

pin recommendation module of Pinterest. We make the ﬁrst

attempt at studying QoS-Aware PPR computation and present

Quota, a system that adapts the state-of-the-art PPR algorithms

to a given environment for minimizing query response time.

Equipped with mathematical tools including queuing theory,

algorithmic complexity analysis, and constrained optimization,

Quota is designed to adapt itself to a wide spectrum of workloads.

We conduct extensive experiments on real datasets and show that

Quota can reduce the query response time compared with state-

of-the-art PPR algorithms, often by a signiﬁcant margin.

I. INTRODUCTION

Given a source node s and a target node t in a graph, the

Personalized PageRank (PPR) π(s, t) reﬂects the probability

that a random walk starting from node s terminates at node t.

PPR is a fundamental proximity measure between two nodes in

graphs, and it has been widely adopted in various applications

such as the Whom-to-Follow service of Twitter [1], the game

service of Tencent [2], and the related-pin recommendation of

Pinterest [3]. As real-world graphs (e.g., in the aforementioned

applications) are dynamically evolving with edge inserts or

deletes, it becomes increasingly important to study efﬁcient

PPR queries on dynamic graphs [4].

When performing PPR queries in dynamically evolving

graphs, it is an intrinsic requirement to simultaneously process

PPR queries and data updates. The data update is not only

about updating the graph but may also involve updating the

index built to facilitate queries. For example, Pinterest uses

PPR queries on its underlying user-item preference graph to

support related-pin recommendations for users, and each page

visit will trigger a PPR query. According to the reports [5],

Pinterest has thousands of page visits per second, demon-

strating a high query workload. Meanwhile, the extensive

user base in Pinterest can lead to frequent updates in the

preference graph, which happens in the same duration as

queries, and ultimately forms a mixture workload of queries

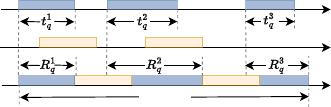
Queries

Updates

Queue

time

Total time

Fig. 1. Timeline of query and update arrivals, as well as the status of the

queue.

and updates. As another example, the online gaming service

of Tencent [6] uses PPR values to measure the proximity

between two game players, where the PPR query is computed

on a game player network formed by players (nodes) and

player interactions (edges). To avoid customer attrition, an

incentive strategy based on PPR has been proven effective in

Tencent [6]. Frequently, a PPR query is issued at the node of

an active player (who regularly uses the service) to sort their

proximity to other inactive players. Those highly-approximate

but inactive players will receive an invite-back message from

the active player. Meanwhile, while applying the incentive

strategy, the player network evolves fast and leads to a mix-

load of PPR queries and data updates. In summary, in real-

world applications based on PPR measures, the workload often

consists of a series of PPR queries and data updates, which

may arrive in a stochastic manner.

In these applications, when the queries and updates arrive

at the system faster than their processing speed, they line up

and form a queue, as shown in Figure 1. The function of the

queue is to ensure that the queries and updates are processed

in a ﬁrst-come-ﬁrst-served (FCFS) manner, which is crucial to

guarantee the query accuracy [4], scheduling fairness [7], and

user fairness [8], [9]. In this queuing context, one important

measure to be optimized is the query response time, which

refers to the amount of time taken between the query’s arrival

at the system and the time at which the query’s answer is

computed, also illustrated as R

in Figure 1. Query response

time is not only determined by the exact query processing

time t

and the processing total time but is also inﬂuenced by

the query/update queuing status. To explain, before a query

can be executed, its previous updates on the graph or indexes

have to be enforced, which can incur a signiﬁcant cost. Hence,

there exists the contention of CPU time between query and

update processing, which often leads to an imbalance of

computing resource allocation between queries and updates.

As the contention intensiﬁes, the user waiting time for queries

can be extended, resulting in lengthy query response time

for the users. In a high-load situation, the queue builds up

quickly, and the response time of a query can be signiﬁcantly

exaggerated, impacting user satisfaction. Therefore, the query

response time closely reﬂects the Quality-of-Service (QoS) to

the user in a PPR-based application.

The problem: QoS-Aware PPR Computations. Despite the

importance of queue-based PPR query response time opti-

mization in practical applications, most of the existing PPR

algorithms [10], [11], [12], [13], [14], [15], [16] focus on a

stand-alone PPR query or update, as reviewed in Section III.

However, the query response time does not solely depend

on query or update processing time, but is more related to

the behavior combination of PPR queries and data updates

in a waiting queue, as we discussed earlier. In this paper,

we make the ﬁrst attempt at PPR computation with a focus

on optimizing the query response time for single-source PPR

(SSPPR) queries or top-k PPR queries over dynamic graphs,

and we name the problem as QoS-Aware PPR Computation.

In particular, given any PPR query and update arrival rates, we

aim to design an algorithmic framework that can adapt itself

to suit the workload in producing a reasonable average query

response time.

QoS-Aware PPR computation is a non-trivial problem. First,

directly applying the state-of-the-art PPR query algorithms

(e.g., Agenda [4], FORA [13]) does not ensure a reasonable

query response time, because they mainly optimize for a

shorter query time at the expense of update time (e.g., updating

index structures). As we have argued, faster query processing

is not necessarily translated into a shorter query response time.

Second, the workload of PPR queries and graph updates may

change over time in recommendation systems. However, the

mainstream PPR algorithms often entail many hyperparam-

eters, making it difﬁcult to set justiﬁable parameters under

different workloads.

These challenges motivate us to design Quota,

a system

that aims to optimize PPR query response time for a wide

spectrum of query and update workload conﬁgurations. We

emphasize several main design philosophies of Quota. First,

our purpose is not to design a faster PPR query algorithm

than existing ones which are already close to the optimum

in many aspects due to the promising development in recent

decades. Instead, given the maturity of the PPR algorithms, it

can be more important to design an algorithmic framework to

accommodate some state-of-the-art PPR algorithms as base

algorithms and allow them to be transparently adapted for

optimizing query response time. In this paper, we discuss three

base algorithms: Agenda [4], FORA [13], and SpeedPPR [16],

because Agenda [4] is the state-of-the-art dynamic PPR al-

gorithm, FORA [13] is a representative PPR algorithm that

motivates many later algorithms, and SpeedPPR is one of the

Quality of Service Optimization for Personalized PageRank over Evolving

Graphs

most query-efﬁcient PPR algorithms in static graphs. Second,

the design of Quota integrates several different branches

of mathematical tools including queuing theory, constrained

optimization, and complexity analysis. Particularly, Quota ab-

stracts the tuning parameters of a typical PPR query framework

and builds a mathematical relationship between the parameters

and the real cost. It then incorporates an in-depth queuing

model to facilitate the transformation of the problem into a

constrained optimization problem. We also design algorithms

to solve the optimization problem to precisely determine the

most suitable parameters for the given workload.

We summarize our main contributions as follows:

• Problem Formulation. We deﬁne the problem of QoS-

Aware PPR optimization, which reﬂects the issues when

applying PPR measures in practical recommendation systems.

The problem is signiﬁcantly different from the existing PPR

optimization problems which optimize a stand-alone PPR

query or update.

• Auto-Conﬁguration System. We present Quota, a con-

ﬁguration system that can be deployed with some state-of-

the-art PPR algorithms to optimize the query response time.

Quota is an auto-conﬁguration system to enhance the state-of-

the-art approach in adaptability to various query and update

workloads. Quota can be applied to four recent state-of-the-art

algorithms, namely, Agenda [4], FORA [13], SpeedPPR [16],

and TopPPR [17]. To the best of our knowledge, Quota is the

ﬁrst conﬁguration system that aims to optimize the PPR query

response time for PPR-based systems.

• Reordering Algorithm. In order to further optimize the

query response time, Quota further allows violation of the

FCFS queuing policy with controllable shufﬂing of the queries

and updates, without affecting the accuracy guarantees. This

forms the reordering algorithm named Seed.

• Extensive Experiments. We have conducted extensive

experiments in various real datasets and settings. Our results

demonstrate that Quota can achieve up to 86%, 40%, 34%,

50% and 33% shorter response time than the state-of-the-

art PPR algorithms Agenda, FORA, SpeedPPR, FORA-TopK

and TopPPR respectively, if deployed with the corresponding

algorithm.

II. PROBLEM DEFINITION

A. PPR Queries

Let G = (V, E) be a directed graph. Given a source node

s ∈ V and a probability α ∈ (0, 1), a random walk from s

is a traversal in G where at each walk step it will move to a

neighbor chosen uniformly at random with probability 1 −α,

and otherwise terminate at the current node. The Personalized

PageRank (PPR) value from s to t, denoted by π(G, s, t),

equals the probability that a random walk starting from s

terminates at t. An important task of PPR computation is the

single-source PPR query, deﬁned as follows.

Deﬁnition 1. (SSPPR queries) Given a source node s, a

threshold δ ∈ (0, 1), an error bound ϵ, and a failure prob-

ability p

, a Single-Source PPR (SSPPR) query returns an

estimated PPR value ˆπ(G, s, t) for each vertex t ∈ V , such

that for any π(G, s, t) > δ, we have:

of 19

免费下载

关注

评论