




ICDE 2025_Collaborative Imputation for Multivariate Time Series with Convergence Guarantee_Apache IoTDB.pdf
100墨值下载
Collaborative Imputation for Multivariate Time
Series with Convergence Guarantee
Yu Sun
†
, Xinyu Yang
†
, Shaoxu Song
∗§
, Ying Zhang
†
, Xiaojie Yuan
†
†
College of Computer Science, DISSec, Nankai University
§
Tsinghua University
{sunyu@, yangxinyu@dbis., yingzhang@, yuanxj@}nankai.edu.cn, sxsong@tsinghua.edu.cn
Abstract—Missing values often occur in multivariate time
series, affecting data analysis and applications. Existing studies
typically use complete data to train imputation models, which
are then used to fill missing values. However, in practice, missing
values could appear in various cells. Such varieties unfortunately
prevent imputation models performing, even making fillings
unavailable without the convergence guarantee, i.e., lacking the
ensurance of obtaining the optimal solution when the itera-
tion tends to infinite. The reasons are that (1) the imputed
values of multiple cells could affect each other towards the
conformance to models, and (2) dependencies obtained from
complete data may not be accurate enough to impute many
unobserved values, which poses a tougher challenge of the
convergence. In this work, we study the collaborative imputation
with the convergence guarantee. By “collaborative”, we mean
(1) all the missing cells can be collaboratively imputed with
the guaranteed conformance to models, and (2) the imputation
models are collaboratively optimized according to fillings as
well. Our major technical highlights include 1) introducing the
statistically explainable collaborative imputation via likelihood
maximization, 2) designing a collaborative imputation algorithm
for multiple missing cells and extending it into a parallel version
equivalently, 3) improving the algorithm by both imputation
values and models collaboratively optimized with the convergence
guarantee in parallel, 4) designing the streaming imputation
and adaptive parameter determination strategies. Experiments
on real incomplete datasets demonstrate the superiority of our
methods against twelve baselines, in both imputation accuracy
and downstream applications.
I. INTRODUCTION
Multivariate time series involve the values over time con-
sisting of multiple attributes, and are very common in the
industrial field [56], [23], [35]. Unfortunately, missing data
are often observed due to sensor failures, network outage,
etc [36]. Analysis of such missing data may create biased
results, misleading downstream applications [55], [28]. Data
imputation is thus a necessary process, and it is not surprising
that various tasks could benefit from the accurate imputation.
A. Motivation
While existing studies have designed diversified imputation
strategies, they still meet intractable challenges of imputing
various missing values in multivariate time series.
(1) Missing values could appear in multiple cells of the
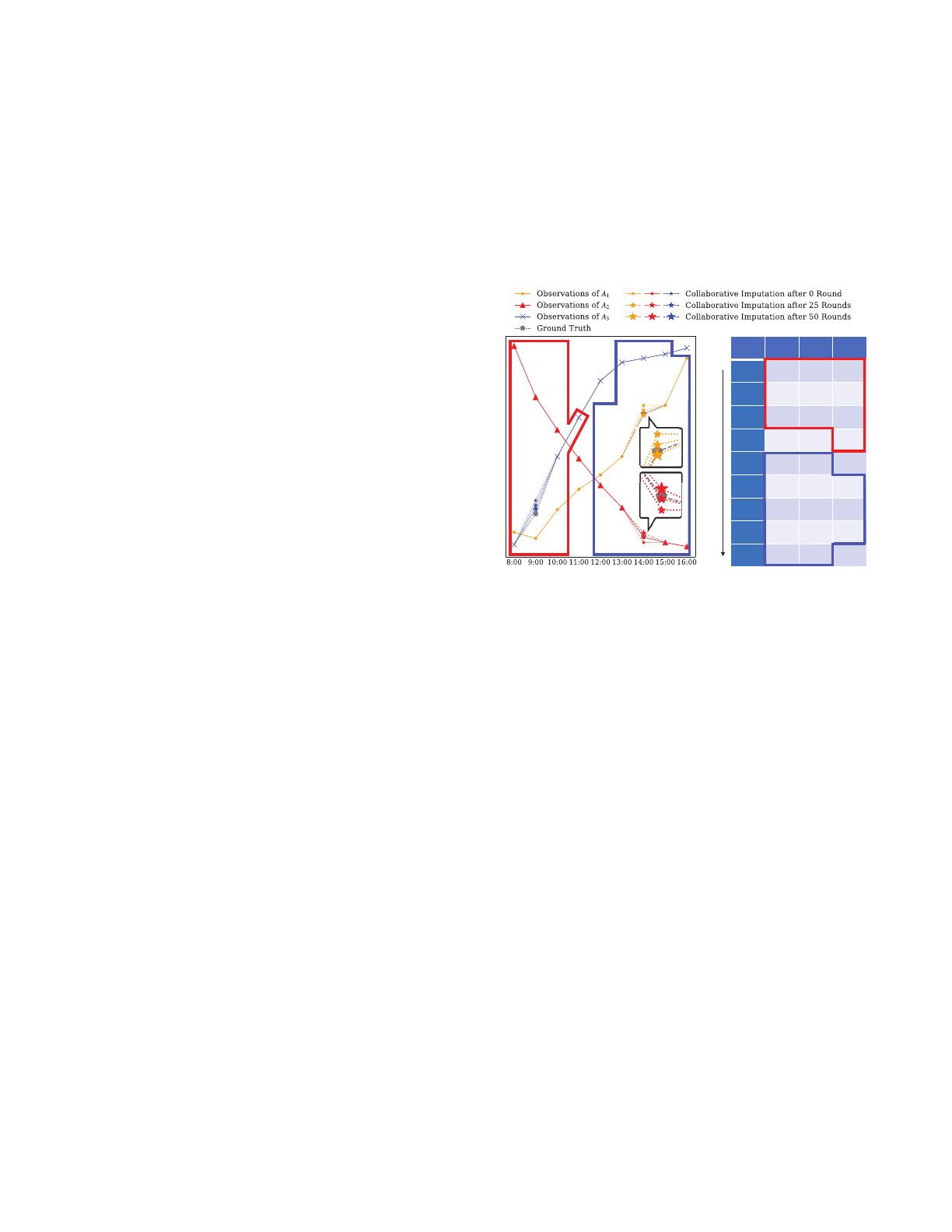
multivariate time series. For instance, Figure 1 illustrates
some example data from the AirQuality dataset on NOx (A
1
),
Humidity (A
2
) and Temperature (A
3
) attributes from 8:00 to
*Shaoxu Song (https://sxsong.github.io/) is the corresponding author.
Fig. 1. Example air quality data with missing values denoted by ⊥, and
imputed by our work after different rounds
16:00 on October 3rd, 2005, with the missing values x
2
[A
3
],
x
7
[A
1
] and x
7
[A
2
]. During this period, the concentration of
NOx increases with the decreasing humidity and the increasing
temperature, i.e., the intratemporal dependency. A statistical
model [42], [69] or temporal rule [2] may use Humidity (A
2
)
and Temperature (A
3
) values to infer the NOx (A
1
) value.
However, since both the determinant (a.k.a. left-hand-side)
attribute x
7
[A
1
] and the dependent (a.k.a. right-hand-side)
attribute x
7
[A
2
] are missing, their imputed values could affect
each other towards conformance to the dependencies between
them. It is thus inaccurate to independently fill them without
considering their mutual effects w.r.t. the convergence guaran-
tee, otherwise we cannot get available fillings conforming to
the dependencies. For instance, if we assign an inappropriate
filling to x
7
[A
2
], it would also be hard to get an accurate
imputation for x
7
[A
1
], following their dependencies.
(2) Existing studies (including both traditional methods
[7], [2], [17] and deep learning techniques [61], [54], [20])
typically train imputation models over complete data, to
capture dependencies and statistics of the entire time series.
However, in practice, there may exist many missing cells,
making the dependencies obtained only from complete data
not accurate enough to impute missing values. Experiments in
Table II show that most imputation methods perform poorly on
datasets with 80% missing values compared to lower missing
rates. Additionally, the convergence guarantee becomes more
1111
2025 IEEE 41st International Conference on Data Engineering (ICDE)
2375-026X/25/$31.00 ©2025 IEEE
DOI 10.1109/ICDE65448.2025.00088

urgent and challenging, with the contradiction of dependencies
between complete data and imputed values. For instance, if
only those complete values in Figure 1 are involved in training
imputation models, they could be insufficient to represent
statistics of missing values x
2
[A
3
], x
7
[A
1
] and x
7
[A
2
].
B. Solution
Considering the aforesaid challenges and limitations of
existing techniques, we study the collaborative imputation with
convergence guarantee to impute missing values in multivari-
ate time series. The benefits are in two aspects.
(1) Both dependent and determinant missing values can
be collaboratively imputed with the convergence guarantee,
rather than filled independently. For instance, as shown in
Figure 1, x
7
[A
1
] and x
7
[A
2
] are collaboratively imputed 50
rounds until convergence, where the fillings become more
accurate with the increasing rounds. Notably, to improve
the imputation efficiency, we further consider the parallel
computation strategies for missing cells involved in disjoint
dependency models. For instance, the red and blue boxes in
Figure 1 represent two distinct imputation contexts that can
be processed parallelly, where the observations within the red
box construct the imputation contexts to impute x
2
[A
3
], and
the observations within the blue box make up the imputation
contexts to fill missing values in x
7
[A
1
] and x
7
[A
2
].
(2) Both missing values and imputation models can be col-
laboratively optimized with the certified convergence, instead
of using fixed models. For instance, not only the complete val-
ues are utilized for the model training, but also the incomplete
cells x
2
[A
3
], x
7
[A
1
] and x
7
[A
2
] are collaboratively involved
in the model optimization according to fillings. That is, our
work can overcome the assumption of existing studies about
the accurate imputation models trained over only complete
data. Moreover, the algorithm is also extended into a parallel
version, where models are asynchronously updated.
Example 1: Figure 1 show some example data from the
AirQuality dataset. Given the temporal window size ω =1,we
establish imputation contexts for missing cells x
2
[A
3
], x
7
[A
1
]
and x
7
[A
2
], as marked in red and blue boxes respectively. To
impute missing values in each box, the most successful and
easy-to-use vector autoregressive (VAR) models [7] can be
employed to capture the dependencies between temporal data
within each designated box, since they are usually used to
model the relationships between adjacent data. The star lines
with different sizes show our collaborative imputation results
after different rounds, where fillings are initialized by recent
attribute values. As for the single missing cell x
2
[A
3
], both
VAR models and our work could obtain a near-optimal filling.
Unfortunately, when there are multiple missing cells x
7
[A
1
],
x
7
[A
2
] in both determinant and dependent attributes, directly
using VAR is no longer available. In contrast, our collaborative
imputation with the convergence guarantee could gradually
compute accurate fillings for them until converged.
The example illustrates that, with the convergence guaran-
teed collaborative imputation, we can optimize both imputa-
tion values and models for the multivariate time series.
Fig. 2. The complete imputation context C
41
and the incomplete C
72
C. Contributions
Our main technical contributions are as follows.
1) We formalize the likelihood of the imputed multivariate
time series w.r.t. dependency models in Section II. The statis-
tically explainable collaborative imputation by the likelihood
is then derived, which demonstrates the rationale of our work.
2) We design a sequential collaborative imputation algo-
rithm towards maximizing the likelihood with the convergence
guarantee (Proposition 1) in Section IV-B. It is further ex-
tended into a parallel version based on whether the imputation
contexts are connected in Section IV-C, which ensures to
return the same result with the sequential algorithm for fixed
updates (Proposition 3).
3) We improve the algorithm with dynamic models to meet
the challenge from many missing values in Section V, whose
convergence is also ensured (Proposition 4). For efficiency,
the algorithm is also improved into a parallel version, with
the convergence guarantee (Propositions 6 and 7) w.r.t. both
fillings and dynamic models.
4) We consider the optimizations of our algorithms in
Section VI, including the streaming imputation for real-time
scenarios and the adaptive parameter determination strategy.
Various real incomplete datasets are employed in experi-
ments in Section VII, verifying the superiority of our work.
II. F
OUNDATIONS
In this section, we first formalize the imputation contexts
and dependency models. The likelihood is then studied for fill-
ings w.r.t. the models. The collaborative imputation for various
missing values, which is statistically explainable referring to
the maximum likelihood estimation, is formally studied.
A. Imputation Contexts and Dependencies
Consider an incomplete multivariate time series I = {x
1
,
...,x
n
} over schema R =(A
1
,...,A
m
), with a timestamp
t
i
for each tuple x
i
∈ I . Each x
i
∈ I contains a collection
of cells {x
i
[A
1
],,...,x
i
[A
m
]}, where x
i
[A
j
], or simply x
ij
,
denotes the value of attribute A
j
in the i-th tuple. The null
cell on attribute A
j
at t
i
is x
ij
= ⊥.Afilling I
of I is also an
instance of R such that existing non-null cells do not change.
To impute missing values in x
i
∈ I , we may refer to
the latest ω tuples, e.g., {x
lj
| i − ω ≤ l < i + ω, 1 ≤
j ≤ m}. Because there may exist both intratemporal and
intertemporal dependencies in multivariate time series. For
instance, in Figure 1, there is the intertemporal dependency
on temperature data over time, as well as the intratemporal
dependency between NOx, humidity and temperature attribute
values. Enlightened by the existing study [57] setting a window
size to repair time series data, we establish the imputation
context for each cell x
ij
, to abstract such dependencies.
1112
of 14
100墨值下载
【版权声明】本文为墨天轮用户原创内容,转载时必须标注文档的来源(墨天轮),文档链接,文档作者等基本信息,否则作者和墨天轮有权追究责任。如果您发现墨天轮中有涉嫌抄袭或者侵权的内容,欢迎发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。
下载排行榜


文档被以下合辑收录
评论