




ICDE 2025_Efficient Structural Clustering over Hypergraphs_OceanBase.pdf
免费下载
Efficient Structural Clustering over Hypergraphs
Dong Pan
∗
, Xu Zhou
∗
, Lingwei Li
∗
, Quanqing Xu
†
,
Chuanhui Yang
†
, Chenhao Ma
‡
, KenLi Li
∗
∗
College of Computer Science and Electronic Engineering, Hunan University, Changsha, China
†
OceanBase, Ant Group, HangZhou, China
‡
The Chinese University of Hong Kong, ShenZhen, China
Email:{pandong, zhxu, lilingwei, lkl}@hnu.edu.cn, {xuquanqing.xqq, rizhao.ych}@oceanbase.com, machenhao@cuhk.edu.cn
Abstract—Structural Graph Clustering is a well-known prob-
lem that aims to identify clusters and distinguish between special
roles, such as hub and outlier. However, SCAN, the fundamental
structural clustering model, is designed for pairwise graphs and
fails to capture the unique structural information inherent in
hypergraphs when clustering hypergraphs. Motivated by this, we
propose a new structural clustering model, HSCAN, specifically
for hypergraphs. We further design an Order-Index to accelerate
fetching the key information of the HSCAN and a Lightweight
Similarity Bucket Index to reduce the index cost. Next, we
present an index-based sequential query algorithm with high
performance and a parallel query algorithm to process large
hypergraphs faster. Additionally, we provide the algorithms for
constructing Order-Index and Lightweight Similarity Bucket
Index. Extensive experiments on both real-world and synthetic
datasets show that HSCAN performs better than existing models,
and the two index-based query algorithms are up to three orders
of magnitude faster than the existing algorithm.
Index Terms—SCAN, graph algorithm, hypergraph, structural
graph clustering
I. INTRODUCTION
Hypergraph is a fundamental graph structure consisting of
hyperedges in which each hyperedge connects an arbitrary
number of nodes, which differs from pairwise graphs where
each edge connects two vertices [1]–[3]. Recently, hypergraphs
have attracted growing attention as they capture higher-order
relationships among multiple entities [1], such as neural net-
works [4], academic networks [5], protein complex networks
[6], and other real-life applications. There has been extensive
research about hypercore maintenance [7], neighborhood-core
decomposition [8], subgraph matching [9], and other problems
[10]–[15]. In this paper, we focus on the structural graph
clustering problem over hypergraphs.
Prior Works. Structural Graph Clustering [16] is a well-
known problem that aims to cluster the vertices based on
structural similarity (e.g., Cosine Similarity [17] or Jaccard
Similarity [18]) and finds clusters, hubs, and outliers. SCAN
[16] is the most fundamental structural clustering model. It
calculates the structural similarity of each vertex pair using
their neighborhoods. Then, SCAN constructs distinct clusters
based on structural similarity scores. Other vertices are iden-
tified as hubs and outliers that do not belong to any cluster,
while hubs bridge different clusters. An example of SCAN is
shown in Fig. 1(a).
Application. Compared to other graph clustering methods,
Structural Graph Clustering has unique outputs (similarity-
based structural clusters, hubs, and outliers), which have a
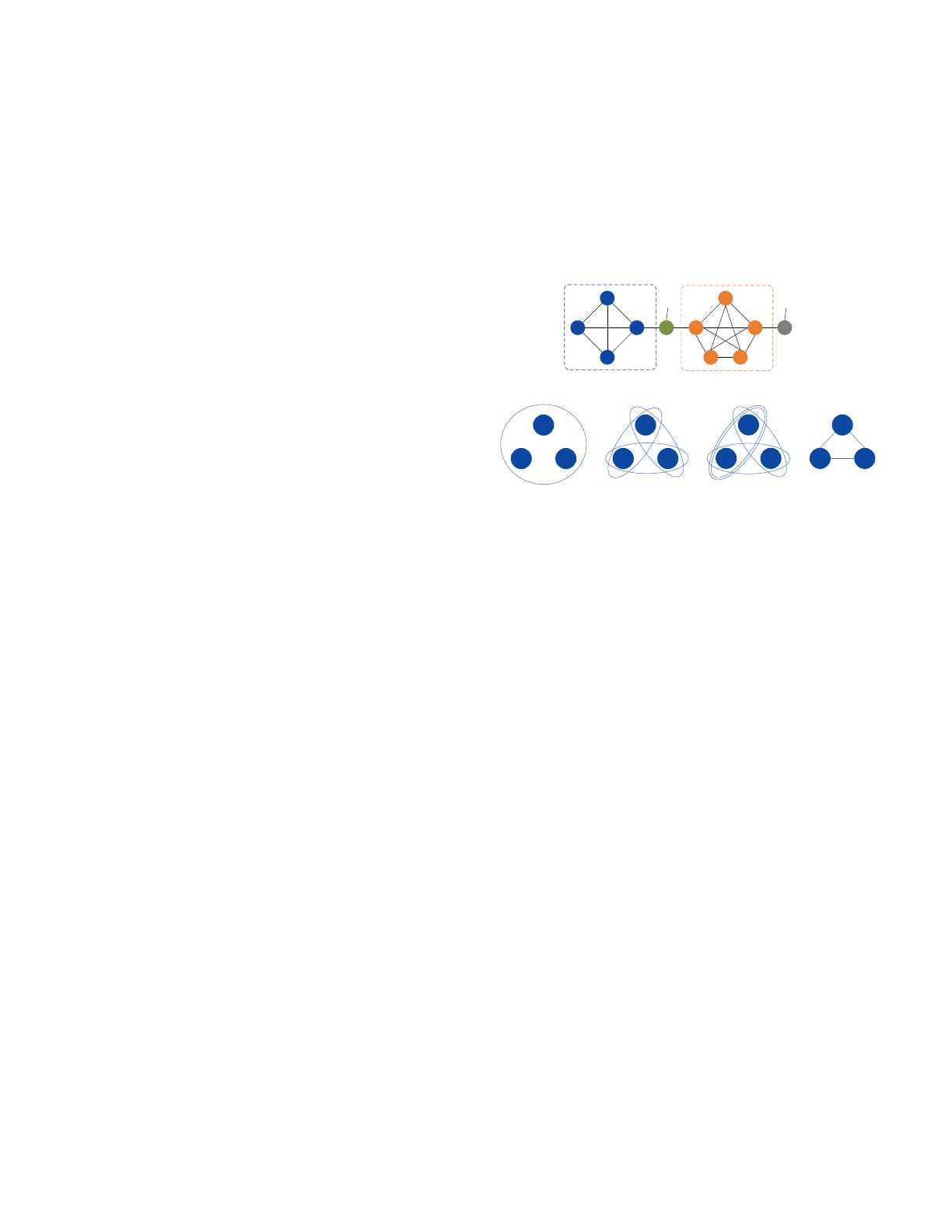
(b) An example of converting different hypergraphs into pairwise graphs.
(a) Hypergraph (b) Pairwise graph (c) Structural information of Fig. 1(c)
G
1
G
2
v
1
v
2
v
3
v
1
v
2
v
3
v
1
v
2
v
3
v
1
v
2
v
3
G
3
G
4
v
1
v
2
v
3
v
4
v
6
v
9
v
8
v
7
v
5
(a) An example of SCAN.
Cluster 1 Cluster 2
hub
outlier
e
1
:1.00, e
3
:0.71, e
4
:0.63, e
2
:0.41
e
2
:1.00, e
3
:0.87, e
4
:0.77, e
1
:0.41
e
3
:1.00, e
4
:0.89, e
2
:0.87, e
1
:0.71
e
4
:1.00, e
3
:0.89, e
2
:0.77, e
1
:0.63, e
7
:0.2
e
5
:1.00, e
6
:0.86, e
7
:0.77
e
6
:1.00, e
7
:0.89, e
5
:0.86
e
7
:1.00, e
6
:0.89, e
5
:0.77, e
4
:0.2
e V(e) Neighbors of e and similarity
e
1
e
2
e
3
e
4
e
5
e
6
e
7
v
1,
v
2
v
1,
v
3,
v
4
v
1,
v
2,
v
3,
v
4
v
1,
v
2,
v
3,
v
4 ,
v
5
v
7,
v
8,
v
9
v
6,
v
7,
v
8 ,
v
9
v
5,
v
6,
v
7,
v
8 ,
v
9
v
1
v
2
v
3
v
4
v
5
v
6
v
7
v
8
v
9
(a) An example of SCAN
(b) An example of converting different hypergraphs into pairwise graphs.
(a) Hypergraph (b) Pairwise graph (c) Structural information of Fig. 1(c)
G
1
G
2
v
1
v
2
v
3
v
1
v
2
v
3
v
1
v
2
v
3
v
1
v
2
v
3
G
3
G
4
v
1
v
2
v
3
v
4
v
6
v
9
v
8
v
7
v
5
(a) An example of SCAN.
Cluster 1 Cluster 2
hub
outliers
e
1
:1.00, e
3
:0.71, e
4
:0.63, e
2
:0.41
e
2
:1.00, e
3
:0.87, e
4
:0.77, e
1
:0.41
e
3
:1.00, e
4
:0.89, e
2
:0.87, e
1
:0.71
e
4
:1.00, e
3
:0.89, e
2
:0.77, e
1
:0.63, e
7
:0.2
e
5
:1.00, e
6
:0.86, e
7
:0.77
e
6
:1.00, e
7
:0.89, e
5
:0.86
e
7
:1.00, e
6
:0.89, e
5
:0.77, e
4
:0.2
e V(e) Neighbors of e and similarity
e
1
e
2
e
3
e
4
e
5
e
6
e
7
v
1,
v
2
v
1,
v
3,
v
4
v
1,
v
2,
v
3,
v
4
v
1,
v
2,
v
3,
v
4 ,
v
5
v
7,
v
8,
v
9
v
6,
v
7,
v
8 ,
v
9
v
5,
v
6,
v
7,
v
8 ,
v
9
v
1
v
2
v
3
v
4
v
5
v
6
v
7
v
8
v
9
(b) Hypergraphs with different hyperedges
Fig. 1. Motivation.
wide range of applications as follows:
• Similarity-based structural clusters have been widely
applied to the analysis of biological data [19]–[22],
social media data [23]–[26], and web data [27]–[29].
In addition, they are useful in image segmentation [30],
image clustering [31], and fraud detection on blockchain
data [32].
• Hubs can be treated as influential nodes and are mean-
ingful in many fields, such as viral marketing [33],
epidemiology [34], and graph compression [35]. Outliers
can be isolated as noise and play a significant role in data
mining [36]–[39].
Motivation. Why not apply SCAN to hypergraphs? Although
SCAN is an effective structural clustering model for undirected
pairwise graphs, it is not effective for other types of graphs
(e.g., directed graphs [40] and uncertain graphs [41], [42]).
When transforming hypergraphs into pairwise graphs to apply
the SCAN model, some similar hypergraphs with different
structural relationships are transformed into the same pairwise
graph, e.g., G
1
, G
2
, and G
3
shown in Fig. 1(b) are all
converted to G
4
. This indicates that a significant amount of
information within the hyperedges is lost when applying
SCAN due to the unique nature of hyperedges.
The following example demonstrates the outcome of apply-
ing SCAN to hypergraphs.
Example 1. 2(a) illustrates an example hypergraph. Fig.
2(b) depicts a pairwise graph converted from the example
hypergraph, and Fig. 2(c) is the structural information of
the example hypergraph. In the pairwise graph, for vertex
v
5
and each of its neighbors v
i
(i ∈ [1 − 4] ∪ [6 − 9]),
the cosine similarity score of their neighborhoods is 0.745.
3480
2025 IEEE 41st International Conference on Data Engineering (ICDE)
2375-026X/25/$31.00 ©2025 IEEE
DOI 10.1109/ICDE65448.2025.00260
BBAAD9C20180234D78A0072836F0B990C2B9B20919647BA0ADD98A36B13C2BEC0B4EB938615C3B0922492408984622EB7DE9210A61D02BE11BBFC25D7A0E32D8241206ADEC2689A794E42A776F674950DD97E0397D6DC37158B6019C534B5CD8DEC62F9B9E3

(b) An example of converting different hypergraphs into pairwise graphs.
(a) Hypergraph (b) Pairwise graph (each edge connects two vertices) (c) Structural information of Fig. 1(c)
G
1
G
2
v
1
v
2
v
3
v
1
v
2
v
3
v
1
v
2
v
3
v
1
v
2
v
3
G
3
G
4
v
1
v
2
v
3
v
4
v
6
v
9
v
8
v
7
v
5
(a) An example of SCAN.
Cluster 1 Cluster 2
hub
outlier
e
1
:1.00, e
3
:0.71, e
4
:0.63, e
2
:0.41
e
2
:1.00, e
3
:0.87, e
4
:0.77, e
1
:0.41
e
3
:1.00, e
4
:0.89, e
2
:0.87, e
1
:0.71
e
4
:1.00, e
3
:0.89, e
2
:0.77, e
1
:0.63, e
7
:0.2
e
5
:1.00, e
6
:0.86, e
7
:0.77
e
6
:1.00, e
7
:0.89, e
5
:0.86
e
7
:1.00, e
6
:0.89, e
5
:0.77, e
4
:0.2
e V(e) Neighbors of e and similarity
e
1
e
2
e
3
e
4
e
5
e
6
e
7
v
1,
v
2
v
1,
v
3,
v
4
v
1,
v
2,
v
3,
v
4
v
1,
v
2,
v
3,
v
4 ,
v
5
v
7,
v
8,
v
9
v
6,
v
7,
v
8 ,
v
9
v
5,
v
6,
v
7,
v
8 ,
v
9
v
1
v
2
v
3
v
4
v
5
v
6
v
7
v
8
v
9
Fig. 2. Example Graphs.
It indicates that v
5
is similar to all other vertex, and SCAN
treats the entire graph as a cluster. It is inappropriate for
hypergraphs, as the structural relationship between two groups
{v
1
, v
2
, v
3
, v
4
, v
5
} and {v
5
, v
6
, v
7
, v
8
, v
9
} involves only two
hyperedges that share a single common vertex. This weak con-
nection contrasts sharply with the stronger internal structural
relationships within each group.
Challenges. There are two main challenges in the structural
clustering of hypergraphs as follows:
• Challenge 1. A new effective structural clustering model
for hypergraphs. The new model should capture the unique
characteristics of hypergraphs and extract the information
carried by hyperedges.
• Challenge 2. An efficient approach for implementing struc-
tural clustering based on the new model. Considering the
hypergraphs in real applications can be large, we need a
new approach that minimizes space overhead while ensuring
rapid implementation of structural clustering.
Our solution. To address Challenge 1, we design a new
hyperedge-centric structural clustering model to facilitate ex-
tracting the structural information contained in hyperedges.
Two hyperedges are considered neighbors if they share at least
one common vertex. For such neighboring hyperedges, we use
a single measure to compute the structural similarity between
the sets of vertices contained in them. Additionally, we replace
vertices with hyperedges in other definitions. Thus, we obtain
a new structural clustering model that effectively captures the
unique characteristics of hypergraphs. We can obtain vertex
clusters directly by this new model. In particular, a vertex
cluster is the set of vertices contained in hyperedges of its
corresponding hyperedge cluster.
Why is a hyperedge-centric structural clustering model
chosen? There are two main reasons leading to the new
hyperedge-centered structural clustering model:
(1) The high-order relationships of vertices are important for
improving the clustering quality in many novel clustering
studies [43]–[46], and the unique structure to represent
the high-order relationships of vertices in hypergraphs
is hyperedge [47]. Thus, the hyperedge-centric model
can gain better clustering results, as demonstrated by the
experiments in Exp-1.
(2) A hyperedge represents a small vertex group (as a clique
in pairwise graphs). Clustering these groups can be
widely utilized in real-life applications, including named
entity recognition systems [48], biomedical research lit-
erature analysis [49], among others.
In summary, a hyperedge-centric model can not only obtain
vertex clusters with high-quality clustering results but also has
a wide range of applications.
To tackle Challenge 2, considering that collecting cores and
similar neighbors are two crucial tasks in structural clustering,
we design an Order-Index to accelerate these collections. To
reduce the cost of Order-Index, we present a Lightweight
Similarity Bucket Index to organize key information into
multiple buckets based on similarity instead of storing the
similarity values. It provides approximate clustering results
with the same query time complexity as Order-Index, which
has a high clustering quality proved theoretically (approximate
guarantee in Theorems 4 and 7) and experimentally (Exp-
9) in this paper. Then, we present two query algorithms,
sequential query algorithm and parallel query algorithm, based
on the indexes proposed in this paper. These query algorithms
efficiently handle the structural clustering within the new
model. Additionally, we present the construction algorithms
for building two indexes.
Contributions. Here are our main contributions:
• We propose a new structural clustering model, HSCAN,
for clustering hypergraphs. HSCAN can capture the unique
structural information of hypergraphs. To the best of our
knowledge, this is the first work on structural clustering for
hypergraphs (Section II).
• We design the Order-Index to boost query performance and
introduce the Lightweight Similarity Bucket Index to reduce
its cost (Section III).
• We propose two index-based query algorithms, sequential
query algorithm, and parallel query algorithm, to efficiently
handle the structural clustering within the new model (Sec-
tion IV).
• We present the construction algorithms for building two
proposed indexes efficiently (Section V).
• Extensive experiments on seven real-world datasets and a
synthetic dataset demonstrate that HSCAN performs better
than other clustering models (Section VI).
II. PRELIMINARIES
A. Problem Definition
In this section, we present the structural hypergraph cluster-
ing model. Table I summarizes frequently used notations and
their meanings.
Notations in hypergraph. We consider an unweighted and
undirected hypergraph G=(V, E) on a finite set of vertices
V , where E ⊂ 2
V
is a set of hyperedges. Each hyperedge
e ∈ E represents a set of |e| vertices that interact. The
hypergraph G can contain hyperedges consisting of only one
3481
BBAAD9C20180234D78A0072836F0B990C2B9B20919647BA0ADD98A36B13C2BEC0B4EB938615C3B0922492408984622EB7DE9210A61D02BE11BBFC25D7A0E32D8241206ADEC2689A794E42A776F674950DD97E0397D6DC37158B6019C534B5CD8DEC62F9B9E3
of 14
免费下载
【版权声明】本文为墨天轮用户原创内容,转载时必须标注文档的来源(墨天轮),文档链接,文档作者等基本信息,否则作者和墨天轮有权追究责任。如果您发现墨天轮中有涉嫌抄袭或者侵权的内容,欢迎发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。
下载排行榜


文档被以下合辑收录
评论