




Turn Waste Into Wealth On Efficient Clustering and Cleaning Over Dirty Data.pdf
100墨值下载
IEEE TRANSACTIONS ON KNOWLEDGE AND DATA ENGINEERING, VOL. 37, NO. 7, JULY 2025 4361
Turn Waste Into Wealth: On Efficient Clustering and
Cleaning Over Dirty Data
Kenny Ye Liang , Yunxiang Su , Shaoxu Song , Senior Member, IEEE, and Chunping Li
Abstract—Dirty data commonly exist. Simply discarding a large
number of inaccurate points (as noises) could greatly affect cluster-
ing results. We argue that dirty data can be repaired and utilized
as strong supports in clustering. To this end, we study a novel
problem of clustering and repairing over dirty data at the same
time. Referring to the minimum change principle in data repairing,
the objective is to find a minimum modification of inaccurate points
such that the large amount of dirty data can enhance clustering.
We show that the problem is
NP-hard and can be formulated as
an integer linear programming (
ILP) problem. A constant factor
approximation algorithm
GDORC is devised based on grid, with
high efficiency. In experiments,
GDORC has great repairing and
clustering results with low time consumption. Empirical results
demonstrate that both the clustering and cleaning accuracies can
be improved by our approach of repairing and utilizing the dirty
data in clustering.
Index Terms—Data repairing, density-based clustering.
I. INTRODUCTION
D
ENSITY-BASED clustering can successfully identify
noises (see a survey in [17]). However, rather than a small
proportion of noise points, real data are often dirty with a large
number of inaccurate points [11]. For instance, a (very) large
portion of GPS data are inaccurate, especially in the indoor
environment with weak signals. According to our experiments
(in Section VI), 1000 out of 3706 (about 27%) GPS readings
are inaccurate. The consequences of such dirty data are sig-
nificant and far-reaching. It can lead to incorrect clustering
results, misidentifying patterns and relationships in the data.
This has serious implications in real-world applications. For
example, in location-based services such as attendance tracking
(see Section VI-G), misidentifications due to uncleaned data can
prevent proper check-ins when clustering. In other applications
like bike-sharing location optimization [3] and traffic anomaly
detection [31], accurate location data is crucial for analysis
and planning. A large portion of uncleaned inaccurate data
undermines the reliability of the analysis and leads to wasted
resources, incorrect decisions, and potential system failures.
Received 13 July 2024; revised 23 February 2025; accepted 16 April 2025.
Date of publication 28 April 2025; date of current version 28 May 2025. This
work was supported in part by the National Natural Science Foundation of China
under Grant 62232005, Grant 62021002, and Grant 92267203, in part by the
National Key Research and Development Plan under Grant 2021YFB3300500,
in part by Beijing National Research Center for Information Science and Tech-
nology under Grant BNR2025RC01011, and in part by Beijing Key Laboratory
of Industrial Big Data System and Application. Recommended for acceptance
by G. Cong. (Corresponding author: Shaoxu Song.)
The authors are with Tsinghua University, Beijing 100190, China (e-mail:
sxsong@tsinghua.edu.cn).
Digital Object Identifier 10.1109/TKDE.2025.3564313
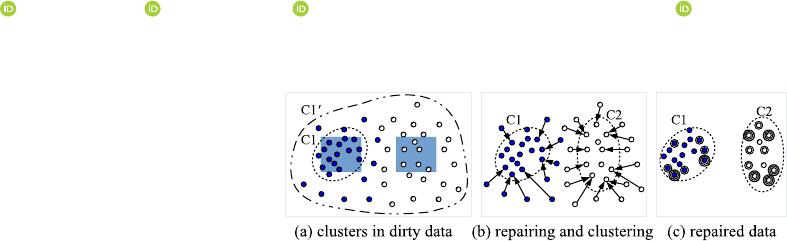
Fig. 1. Clustering with repairing over dirty data.
The large amount of noise points are simply discarded, if we
directly apply the existing density-based clustering approaches,
e.g., the well-known
DBSCAN [7]. With too much information
loss, clustering results could be dramatically affected (see ex-
amples below).
A. Motivation
Instead of discarding dirty data, we argue that dirty data can be
repaired and utilized as strong supports in clustering. Study [29]
shows that performing data cleaning and clustering at the same
time leads to better performance.
We propose repairing dirty data based on density informa-
tion, inspired by its effectiveness in identifying noisy data in
density-based clustering. The approach simultaneously repairs
data according to its density during clustering, allowing both
tasks to benefit (as shown in Section VI).
Following the minimum change principle in data repair-
ing [33]—where changes made during repairs are minimized—
the objective of simultaneous repairing and clustering is to
achieve the smallest possible data repair, enabling effective
utilization of all data for clustering. The rationale is based on
the practical intent to minimize errors, as dirty data, such as
inaccurate GPS readings, are typically close to their true values.
Guided by this objective, we define the problem as an optimiza-
tion problem, namely Density-based Optimal Repairing and
Clustering (
DORC).
Example 1: We illustrate an example of GPS data in Fig. 1,
showing readings from two nearby buildings marked as blue and
white points. Cluster C1 represents high-density, precise points
from a building with strong GPS signal, while C2 shows inac-
curate points from a building with weak GPS signal requiring
focused repair. Density-based clustering methods like
DBSCAN
either generate cluster C1 (with high-density parameters) or C1
(with low-density parameters). The white points from the second
building fail to form a separate cluster, either being treated as
noise in C1 or merged with blue points in C1
. Points identified as
1041-4347 © 2025 IEEE. All rights reserved, including rights for text and data mining, and training of artificial intelligence and similar technologies.
Personal use is permitted, but republication/redistribution requires IEEE permission. See https://www.ieee.org/publications/rights/index.html for more information.
Authorized licensed use limited to: Tsinghua University. Downloaded on July 28,2025 at 07:57:48 UTC from IEEE Xplore. Restrictions apply.
4362 IEEE TRANSACTIONS ON KNOWLEDGE AND DATA ENGINEERING, VOL. 37, NO. 7, JULY 2025
noises by DBSCAN in Fig. 1(a) strongly suggest the need to focus
on refining C2. (See more examples in Fig. 8 in Section VI).
In this study, we propose to repair the inaccurate data points
during clustering. For example, as shown in Fig. 1(b),anarrow
(a → b) denotes that a point is repaired from location a to
location b. Since points are concentrated after repairing, two
clusters are formed in Fig. 1(c).
The problem of clustering with repairing, however, is non-
trivial. Simply repairing noise points to the closest clusters is
not sufficient, e.g., repairing all the noise points to C1 in Fig. 1
does not help in identifying the second cluster C2. It should
be considered that dirty points may possibly form clusters with
repairing (i.e., C2).
Clustering and cleaning data provide significant benefits in
various real-world applications. For example, in personal at-
tribute analysis [26], cleaning GPS data improves clustering
accuracy, enhancing the interpretation of regional studies. In
healthcare [20], cleaning GPS data enhances the clustering of
lifelog data, ensuring better accuracy in identifying individuals’
activity patterns. In location-based services [31], cleaning GPS
data ensures correct coordinates, which is crucial for accurate
clustering in tasks such as attendance tracking and urban plan-
ning. As shown in Figs. 9 and 10 of application study, cleaning
enhances the accuracy and reliability of location-based services
like attendance tracking.
B. Contribution
Our proposed DORC techniques complement existing repair
methods. Compared to these methods (details in Section II),
DORC has two major advantages: (1) it does not rely on external
knowledge of integrity constraints or rules, and (2) it utilizes
the density information embedded within the data, which many
methods overlook.
This paper focuses on the grid-based
GDORC algorithm, which
simultaneously repairs and clusters with a constant factor ap-
proximation. Compared to
QDORC and LDORC [29], GDORC
achieves comparable accuracy but with reduced time, as it
searches data cells instead of individual points.
Our major contributions in this paper are summarized as:
1) We formalize the
DORC problem of simultaneous cluster-
ing and repairing (presented in Section III). In particular,
no additional parameters are introduced for
DORC besides
the density and distance thresholds η and ε for clustering.
2) We provide the hardness analysis and tractable special
case for the
DORC problem, and formulate DORC as an ILP
problem (detailed in Section IV).
3) We devise a constant factor approximation method,
GDORC, based on a grid that decomposes the data space
into cells (described in Section V). The correctness and the
complexity of the algorithm are analyzed in Propositions 6
and 7, respectively. Furthermore, the approximation ratio
of
GDORC is examined in Proposition 8.
4) We conduct extensive experiments on real datasets (illus-
trated in Section VI ). The results demonstrate that our
proposed
GDORC approach has both high clustering and
repairing performances, while keeping time costs low.
Full proofs of major results can be found at [18].
II. R
ELATED WORK
A. Clustering
Density-based clustering is widely used (see [17]). Given
a distance threshold ε and a minimum neighborhood size η
(MinPts),
DBSCAN [7] categorizes points into cores, borders,
and noise. In this study, we adhere to these established set-
tings. Numerous algorithms elaborate on the concept of
DB-
SCAN. Various versions of DBSCAN have been developed, in-
cluding the incremental version [6], the distributed version NG-
DBSCAN [21] and DBSCAN-MS [34], and the dynamic ver-
sion [9].
DBSCAN++ [13] aims to reduce computational cost by
estimating densities for subsets of points.
DBSVEC [32] integrates
support vectors to reduce unnecessary range queries, enhancing
efficiency.
ANYDBC [22] compresses data into subsets and labels
objects based on connected components to reduce time cost.
DBSCAN-DIST [1] combines the concepts of density and minimax
distance to formalize density-based clustering by a loss function.
Several methods focus on stream data. DISC [16] intro-
duces a density-based incremental strategy with elaborations
on points’ types, including ex-cores and neo-cores. D
ENFOR-
EST [15] presents a concept of ”nostalgic core” and uses spanning
trees for better cluster quality and efficiency.
All these studies focus primarily on identifying noise/non-
noise points, while the large amount of dirty data (identified as
noises) are still not employed to form clusters. In contrast, our
proposal considers cleaning and clustering with dirty data. While
outlier detection (see [12] for a survey) identifies dirty points,
data repairing further modifies these points for correction. In-
deed, our proposal incorporates density-based
DBSCAN.Inthis
sense, data repairing and outlier detection are complementary.
B. Repairing
Besides the minimum modification model [33], which we
also adopt, t he deletion model [4] is commonly used to identify
the minimum removal of dirty data. In this context,
DBSCAN
can be seen as a deletion-based technique, eliminating dirty
data. However, simply discarding large amounts of dirty data
as noise using existing clustering methods is not ideal and can
significantly affect clustering results.
Recent data repair methods, such as
HOLOCLEAN [5], IMR [35],
RSR [19], and MISC [28], address data errors in various ways.
H
OLOCLEAN integrates multiple data sources to detect and repair
anomalies, but relies on external data and integrity constraints.
IMR is an incremental regression method for time-series data,
which is less effective for static data. RSR uses regular ex-
pressions to repair s equence and token values, but requires
predefined rules.
Our study, as mentioned in the introduction, focuses on the
density information within the data, without relying on ex-
ternal knowledge or constraints. Our approach complements
these techniques when additional information, such as rules,
is available. MISC repairs data errors on selected attributes
but is less suited for datasets like GPS data, where errors im-
pact both longitude and latitude simultaneously. Therefore, we
perform full-feature repairs directly on GPS data, where MISC’s
advantages are less applicable.
Authorized licensed use limited to: Tsinghua University. Downloaded on July 28,2025 at 07:57:48 UTC from IEEE Xplore. Restrictions apply.
of 12
100墨值下载
【版权声明】本文为墨天轮用户原创内容,转载时必须标注文档的来源(墨天轮),文档链接,文档作者等基本信息,否则作者和墨天轮有权追究责任。如果您发现墨天轮中有涉嫌抄袭或者侵权的内容,欢迎发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。
下载排行榜


评论