2025 ICDE_-HC-SpMM_Accelerating_Sparse_Matrix-Matrix_Multiplication_for_Graphs_with_Hybrid_GPU_Cores.pdf

Whill

14页

0次

2025-10-28

免费下载

HC-SpMM: Accelerating Sparse Matrix-Matrix

Multiplication for Graphs with Hybrid GPU Cores

Zhonggen Li

∗

, Xiangyu Ke

∗†

, Yifan Zhu

∗†

, Yunjun Gao

∗†

, Yaofeng Tu

‡

∗

Zhejiang University,

†

Zhejiang Key Laboratory of Big Data Intelligent Computing,

‡

ZTE Corporation

{zgli, xiangyu.ke, xtf z, gaoyj}@zju.edu.cn, tu.yaofeng@zte.com.cn

Abstract—Sparse Matrix-Matrix Multiplication (SpMM) is

a fundamental operation in graph computing and analytics.

However, the irregularity of real-world graphs poses signiﬁcant

challenges to achieving efﬁcient SpMM for graph data on GPUs.

Recently, the introduction of new efﬁcient computing cores within

GPUs offers new opportunities for acceleration.

In this paper, we present HC-SpMM, a pioneering algorithm

that leverages Hybrid GPU Cores (Tensor cores and CUDA cores)

to accelerate SpMM for graphs. To adapt to the computing

characteristics of different GPU cores, we investigate the impact

of sparse graph features on the performance of different cores,

develop a data partitioning technique for the graph adjacency

matrix, and devise a novel strategy for intelligently selecting the

most efﬁcient cores for processing each submatrix. Additionally,

we optimize it by considering memory access and thread uti-

lization. To support complex graph computing workloads, we

integrate HC-SpMM into the GNN training pipeline. Further-

more, we propose a kernel fusion strategy to enhance data

reuse, as well as a cost-effective graph layout reorganization

method to mitigate the irregularity of real-world graphs, better

ﬁtting the computational models of hybrid GPU cores. Extensive

experiments on 14 real-world datasets demonstrate that HC-

SpMM achieves an average speedup of 1.33× and 1.23× over

state-of-the-art SpMM kernels and GNN frameworks.

Index Terms—GPU cores, SpMM, Graph Computing

I. INTRODUCTION

Sparse Matrix-Matrix Multiplication (SpMM) is a funda-

mental operation that multiplies a sparse matrix and a dense

matrix, which has been widely used in various graph comput-

ing tasks such as Graph Neural Networks (GNNs) training &

inference [9], [28], [62], PageRank [21], [29], [37] and graph

clustering [4], [14], [53], [59]. Recent studies employ matrix

multiplication operations on GPUs to accelerate commonly

used graph algorithms such as triangle counting and shortest

path computing, with SpMM emerging as one of the core

operations and becoming the efﬁciency bottleneck [40], [57].

SpMM is also a fundamental operation in GNNs, accounting

for more than 80% of the GNN training time [47]. However,

characterized by irregular memory access patterns and low

computational intensity, the real-world graphs pose signiﬁcant

challenges for achieving efﬁcient SpMM on GPU [47]. Es-

pecially for GNNs, as the scale of graph data proceeds to

grow and the complexity of GNN architectures escalates with

an increasing number of layers, the efﬁciency issue becomes

more serious, constraining the large-scale applicability

, even

Training a GNN-based recommendation system over a dataset comprising

7.5 billion items consumes approximately 3 days on a 16-GPU cluster [10].

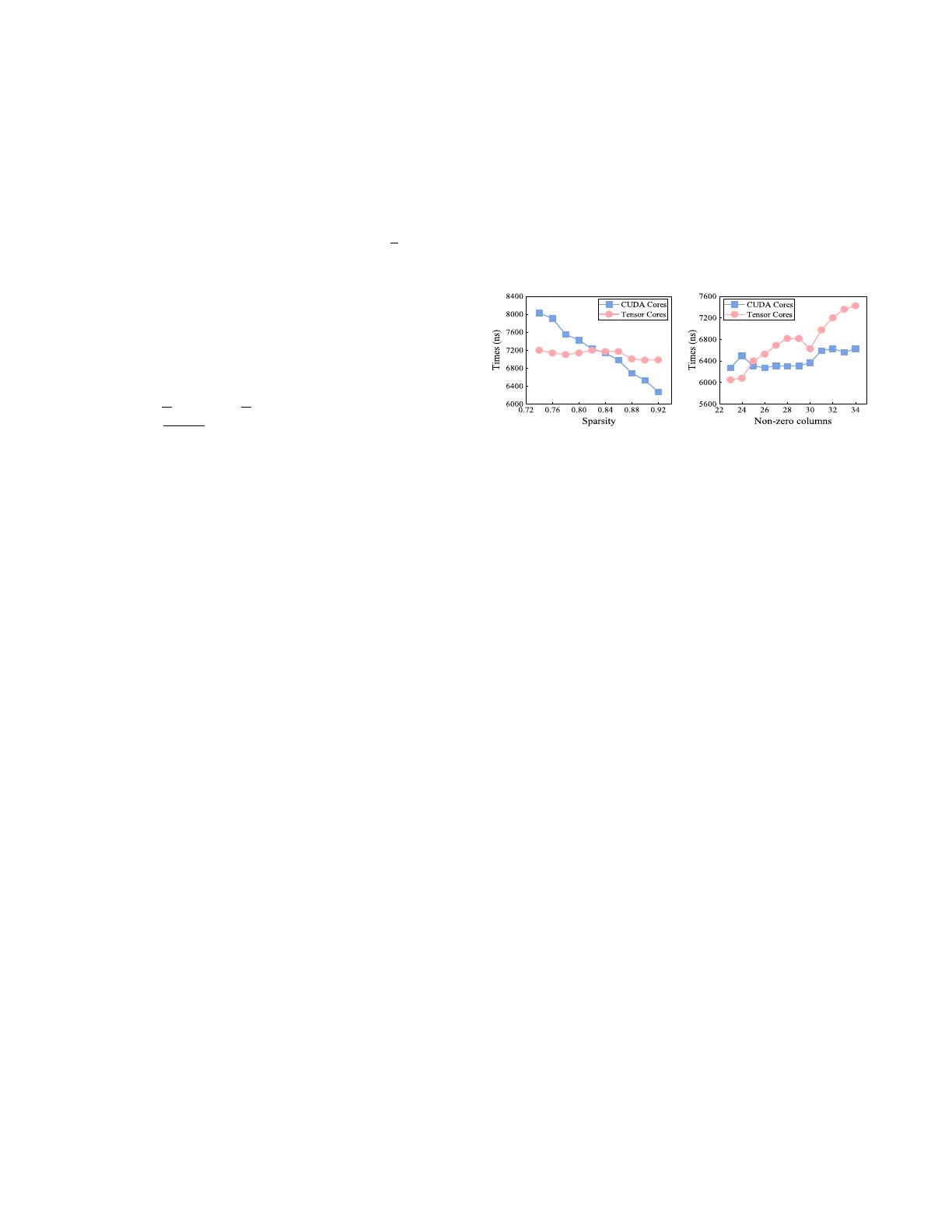
(a) Varying sparsity. (b) Varying non-zero columns.

Fig. 1. SpMM execution time with varying sparsity and non-zero columns.

though it achieves state-of-the-art performance on a myriad

of problems such as node classiﬁcation [38], [48], [61], link

prediction [18], [35], [64], [68], recommendation [49], [51],

[60] and beyond [5], [13], [26], [39].

To enhance the efﬁciency of SpMM, some efforts have been

made to employ CUDA cores in GPU for acceleration [16],

[20], [23], [32]. As the performance ceil is constrained by

the hardware structure of CUDA cores, recent attempts have

turned to explore harnessing the Tensor cores, which are

specialized for efﬁcient matrix multiplication, to accelerate

SpMM [6], [27], [58]. However, despite signiﬁcantly improv-

ing the efﬁciency of dense matrix multiplication [30], the

irregularity and sparsity of real-world graphs impeding Tensor

cores from achieving satisfactory performance [12], [47], [58].

Various preprocessing techniques have been investigated to

enhance the density of sparse matrices, yet signiﬁcant sparse

portions persist, hindering performance improvement

Figure 1 illustrates the time overhead incurred by CUDA

cores and Tensor cores across matrices with varying sparsity

and the number of non-zero columns, which highlights their

distinct applicabilities

. CUDA cores demonstrate superior

performance when handling sparser matrices with a higher

number of non-zero columns, whereas Tensor cores exhibit

greater efﬁcacy in denser matrices characterized by fewer

non-zero columns. Thereafter, relying solely on CUDA cores

or Tensor cores for SpMM acceleration fails to fully exploit

their respective computational strengths, primarily due to the

irregularity of real-world graphs, which typically comprise a

mixture of dense and sparse regions [55].

In this paper, we aim to devise a graph-friendly SpMM

kernel using hybrid CUDA cores and Tensor cores, tailored

For instance, the average sparsity of the matrices output by the preprocess-

ing method proposed in TC-GNN [47] is still 90.9% on 10 tested datasets.

An in-depth analysis is provided in § IV-C.

501

2025 IEEE 41st International Conference on Data Engineering (ICDE)

DOI 10.1109/ICDE65448.2025.00044

Authorized licensed use limited to: ZTE Corporation (One Dept). Downloaded on October 28,2025 at 06:54:20 UTC from IEEE Xplore. Restrictions apply.

to the varying computational demands of different graph

regions, to support high-performance graph computing work-

loads. Furthermore, as a DB technique for AI acceleration,

we integrate the hybrid SpMM kernel into the GNN training

pipeline to enhance the training efﬁciency and demonstrate its

effectiveness in complex graph computing scenarios.

However, crafting a hybrid SpMM kernel using CUDA

cores and Tensor cores based on the characteristics of graph

data and systematically integrating it into the GNN training

pipeline encounters non-trivial challenges.

Challenges of designing hybrid SpMM kernel. (1) Ef-

fectively partitioning the adjacency matrix into sub-regions

with distinct sparsity characteristics to leverage the different

cores for collaborative computation presents a considerable

challenge. (2) The computational characteristics of CUDA and

Tensor cores vary signiﬁcantly, which is also inﬂuenced by the

graph features, making the selection of the optimal core for

matrices with different sparsity levels crucial for enhancing

efﬁciency. (3) Accurately modeling the computational perfor-

mance of CUDA and Tensor cores for SpMM to facilitate

precise core selection is another major difﬁculty. (4) Last but

not least, inefﬁciencies inherent in the SpMM kernel, such as

suboptimal memory access patterns and underutilized threads,

limit the overall performance. To address these issues, we

ﬁrstly propose a ﬁne-grained partition strategy, which divides

the adjacency matrix into equal-sized submatrices along the

horizontal axis, allocating each submatrix to the appropriate

GPU cores for efﬁcient computation (§ IV-A). This allows

CUDA and Tensor cores to perform calculations indepen-

dently, eliminating the need to merge results between cores.

Secondly, comprehensive quantitative experiments reveal that

CUDA cores are memory-efﬁcient while Tensor cores are

computing-efﬁcient (§ IV-B). These experiments identify two

pivotal factors for submatrix characterization: sparsity and

the number of non-zero columns, which dominate the most

expensive parts for CUDA and Tensor cores, computation and

memory access, respectively. Thirdly, leveraging these factors,

we develop an algorithm tailored for the selection of appro-

priate GPU cores for submatrices, optimizing computational

capability (§ IV-B). Finally, we conduct in-depth optimiza-

tions of the SpMM kernel, considering thread collaboration

mode (§ IV-D1) and memory access patterns (§ IV-D2).

Challenges of integrating the SpMM kernel into GNN.

When integrating our proposed hybrid SpMM kernel into the

GNN training pipeline, there arise new challenges. (1) The

isolation among GPU kernels within a GNN layer in prevalent

GNN training frameworks [43], [47] impedes data reuse,

leads to additional memory access overhead, and introduces

signiﬁcant kernel launch overhead. (2) Tensor cores incur

signiﬁcantly higher throughput than CUDA cores, potentially

offering substantial efﬁciency gain. However, real-world graph

layouts inherently exhibit irregularity and sparsity, resulting in

a majority of segments partitioned from the adjacency matrix

being sparse and less amenable to processing via Tensor cores.

Consequently, the performance gains achievable with Tensor

cores are often negligible [47]. To tackle the ﬁrst problem,

we discover opportunities to reuse data in the shared memory

of GPU and present a kernel fusion strategy to mitigate

kernel launch costs and global memory access (§ V-A). To

address the second problem, we ﬁrst introduce a metric termed

computating intensity to estimate the calculation workload of

the submatrices multiplication (§ V-B), which is calculated

by the quotient of the number of non-zero elements and the

number of non-zero columns. Higher computational intensity

is achieved with more non-zero elements and fewer non-

zero columns. Subsequently, we propose an efﬁcient algorithm

to reconstruct submatrices, adjusting the graph layouts to

obtain more dense segments suitable for processing by Tensor

cores, gaining signiﬁcant efﬁciency with Tensor cores (§ V-B).

This adjustment has a relatively small cost compared with

GNN training but renders the graph data more compatible

with hybrid GPU cores, unlocking the full computational

potential of Tensor cores and thereby signiﬁcantly enhancing

the efﬁciency of GNN training (§ VI-C3).

Contributions. In this work, we propose HC-SpMM, a novel

approach for accelerating SpMM using hybrid GPU cores. Our

key contributions are summarized as follows:

• We quantify the difference between CUDA and Tensor

cores in SpMM, and propose a hybrid SpMM kernel,

which partitions the graph adjacency matrix and intelli-

gently selects appropriate GPU cores for the computation

of each submatrix based on its characteristics. We further

optimize the SpMM kernel considering thread collabora-

tion mode and memory access patterns (§ IV).

• We propose a kernel fusion strategy for integrating HC-

SpMM into the GNN training pipeline, eliminating kernel

launch time and enabling efﬁcient data reuse, and present

a lightweight graph layout optimization algorithm to

enhance irregular graph layouts and better align with the

characteristics of both GPU cores (§ V).

• We conduct comprehensive evaluations demonstrating

that HC-SpMM outperforms existing methods, achieving

1.33× speedup in SpMM and 1.23× speedup in GNN

training on average (§ VI).

The rest of this paper is organized as follows. Section II

reviews the related work. Section III gives the preliminaries.

Section IV presents the design of the hybrid SpMM kernel.

Section V describes the optimization of integrating the SpMM

kernel into GNNs. Section VI exhibits the experimental results.

We conclude the paper in Section VII.

II. RELATED WORK

SpMM Using CUDA Cores. Optimization of SpMM has

been a subject of extensive study [3], [20], [50], [56], [65].

In recent years, Yang et al. [56] leveraged merge-based load

balancing and row-major coalesced memory access strategies

to accelerate SpMM. Hong et al. [20] designed an adap-

tive tiling strategy to enhance the performance of SpMM.

cuSPARSE [32] offers high-performance SpMM kernels and

has been integrated into numerous GNN training frameworks

such as DGL [43]. Gale et al. point out that cuSPARSE

is efﬁcient only for matrices with sparsity exceeding 98%.

502

Authorized licensed use limited to: ZTE Corporation (One Dept). Downloaded on October 28,2025 at 06:54:20 UTC from IEEE Xplore. Restrictions apply.

of 14

免费下载

关注

评论