Probabilistic Prediction of Vehicle Semantic Intention and Motion.pdf

Libria

257

7页

0次

2021-02-22

50墨值下载

Probabilistic Prediction of Vehicle Semantic Intention and Motion

Yeping Hu, Wei Zhan and Masayoshi Tomizuka

Abstract— Accurately predicting the possible behaviors of

trafﬁc participants is an essential capability for future au-

tonomous vehicles. The majority of current researches ﬁx the

number of driving intentions by considering only a speciﬁc

scenario. However, distinct driving environments usually con-

tain various possible driving maneuvers. Therefore, a intention

prediction method that can adapt to different trafﬁc scenarios

is needed. To further improve the overall vehicle prediction

performance, motion information is usually incorporated with

classiﬁed intentions. As suggested in some literature, the meth-

ods that directly predict possible goal locations can achieve

better performance for long-term motion prediction than other

approaches due to their automatic incorporation of environment

constraints. Moreover, by obtaining the temporal information of

the predicted destinations, the optimal trajectories for predicted

vehicles as well as the desirable path for ego autonomous vehicle

could be easily generated. In this paper, we propose a Semantic-

based Intention and Motion Prediction (SIMP) method, which

can be adapted to any driving scenarios by using semantic-

deﬁned vehicle behaviors. It utilizes a probabilistic framework

based on deep neural network to estimate the intentions,

ﬁnal locations, and the corresponding time information for

surrounding vehicles. An exemplar real-world scenario was

used to implement and examine the proposed method.

I. INTRODUCTION

Safety is the most fundamental aspect to consider for both

human drivers and autonomous vehicles. Human drivers are

capable of using past experience and intuitions to avoid

potential accidents by predicting the behaviors of other

drivers. However, some drivers have poor driving habits such

as changing lanes without using turn signals, which adds dif-

ﬁculties for prediction. Moreover, human drivers might easily

overlook dangerous situations due to limited concentration.

Therefore, the Advanced Driver Assistance Systems (ADAS)

should have the ability to simultaneously and accurately

anticipate future behaviors of multiple trafﬁc participants

under various driving scenarios, which may then assure a

safe, comfortable and cooperative driving experience.

There have been numerous works focused on predicting

vehicle behavior which can be divided into two categories:

intention/maneuver prediction and motion prediction.

Many intention estimation problems have been solved by us-

ing classiﬁcation strategies, such as Support Vector Machine

(SVM) [1], Bayesian classiﬁer [2], Multilayer Perceptron

(MLP) [3], and Hidden Markov Models (HMMs) [4]. Most

of these approaches were only designed for one particular

scenario associated with limited intentions. For example,

[1]-[3] dealt with non-junction segment such as highway,

*This work was supported by Berkeley DeepDrive (BDD).

Y. Hu, W. Zhan and M. Tomizuka are with the Department of Me-

chanical Engineering, University of California, Berkeley, CA 94720 USA

[yeping

hu, wzhan, tomizuka@berkeley.edu]

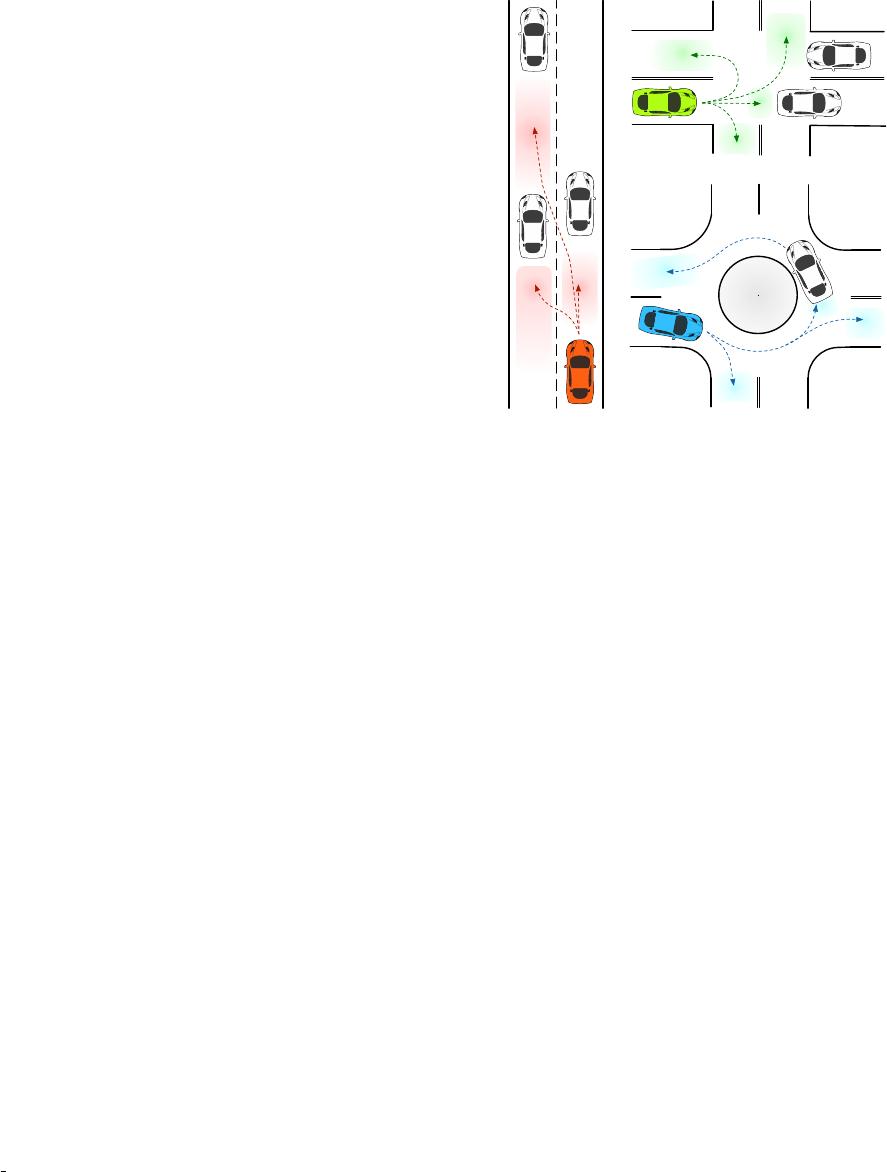
Fig. 1. Insertion areas (colored regions) under different driving scenarios

for the predicted vehicle.

which involves lane keeping (LK), lane change left (LCL)

and lane change right (LCR) maneuvers. Whereas [4]-[6]

concentrated on junction segment such as intersection, which

includes left turn, right turn, and go straight maneuvers.

However, in order for autonomous vehicles to drive through

dynamically changing trafﬁc scenes in real life, an intention

prediction module that can adapt to different scenarios with

various possible driving maneuvers is necessary. [7] proposed

a maneuver estimation approach for generic trafﬁc scenarios,

but the classiﬁed driving maneuvers are too speciﬁc, which

will not only require multiple manually-selected classiﬁca-

tion thresholds, but also raise problems when unclassiﬁed

maneuvers occur.

As a result, we proposed to use semantics to represent

the driver intention, which is deﬁned as the intent to enter

each insertion area. These areas can be the available gaps

between any two vehicles on the road or can be the lane

entrances/exits. Fig. 1 visualizes the insertion areas under

distinct environments. An advantage of using semantic ap-

proach is that situations can be modeled in a uniﬁed way

[8] such that varying driving scenarios will have no effect

on our semantics deﬁned problem. Even for a scenario that

has a combination of all the road structures in Fig. 1, the

proposed semantic deﬁnition still holds.

Motion prediction is mostly treated as a regression prob-

lem, where it tries to forecast the short-term movements and

long-term trajectories of vehicles. By incorporating motion

2018 IEEE Intelligent Vehicles Symposium (IV)

Changshu, Suzhou, China, June 26-30, 2018

prediction with intention estimation, not only the high-

level behavioral information, but also the future state of the

predicted vehicle can be obtained. For short-term motion

prediction, various approaches such as constant acceleration

(CA), Intelligent Driver Model (IDM) [6], and Particle Filter

(PF) [9] have been suggested. The main limitation of these

works, however, is that they either considered simple cases

such as car following or did not take environment informa-

tion into account.

For future trajectory estimation, Dynamic Bayesian Net-

works (DBN) [10] and other regression models [11] have

been used in several studies. Methods based on artiﬁcial

neural network (ANN) are also widely applied. In [12],

the authors used the LSTM to predict the vehicle trajec-

tory in highway situation. [13] brought forward a Deep

Neural Networks (DNN) to obtain the lateral acceleration

and longitudinal velocity. However, these approaches only

predicted the most likely trajectory for the vehicle without

considering uncertainties in the environment. To counter this

issue, a Variational Gaussian Mixture Model (VGMM) was

proposed for probabilistic long-term motion prediction [14].

Nevertheless, the method was only tested in a simulation

environment and the input contains history information over

a long period of time, which is usually unaccessible in

reality. There are also researches that project the prediction

step of a tracking ﬁlter forward over time, but the growing

uncertainties often cause future positions to end up at some

physically impossible locations.

In contrast, works such as [15] and [16] highlighted

that by predicting goal locations and assuming that agents

navigate toward those locations by following some optimal

paths, the accuracy of long-term prediction can be improved.

The main advantage of postulating destinations instead of

trajectories is that it allows one to represent various dynamics

and to automatically incorporate environment constraints for

unreachable regions.

Apart from obtaining the possible goals of predicted

vehicles, the required time to reach those locations is also an

essential information especially for the subsequent trajectory

planning of the ego vehicle. Therefore, many attempts have

been made in order to directly predict temporal information.

[17] used LSTM to forecase time-to-lane-change (TTLC)

of vehicles under highway scenarios. A recent work [18]

utilized the Linear Quantile Regression (LQR) and Quantile

Regression Forests (QRF) methods for the probabilistic re-

gression task of TTLC. The authors also concluded that QRF

has better performance than LQR.

In this paper, Semantic-based Intention and Motion Pre-

diction (SIMP) method is proposed. It utilizes deep neural

network to formulate a probabilistic framework which can

predict the possible semantic intention and motion of the

selected vehicle under various driving scenarios. The intro-

duced semantics for this prediction problem is deﬁned as

answering the question of ”Which area will the predicted

vehicle most likely insert into? Where and when?”, which

incorporates both the goal position and the time information

into each insertion area. Moreover, the adoption of probabil-

ity can take into account the uncertainty of drivers as well

as the evolution of the trafﬁc situations.

The remainder of the paper is organized as follows: Sec-

tion II provides the concept of the proposed SIMP method;

Section III discusses an exemplar scenario to apply SIMP;

evaluations and results are provided in Section IV; and

Section V concludes the paper.

II. CONCEPT OF SEMANTIC-BASED INTENTION AND

MOTION PREDICTION (SIMP)

In this section, we ﬁrst provide a brief overview of Mixture

Density Network (MDN), which is an idea we utilize for

our proposed method. Then, the detailed formulation and

structure of the SIMP method are illustrated.

A. Mixture Density Network (MDN)

Mixture Density Network is a combination of ANN and

mixture density model, which was ﬁrst introduced by Bishop

[19]. The mixture density model can be used to estimate the

underlying distribution of data, typically by assuming that

each data point has some probability under a certain type of

distribution. By using a mixture model, more ﬂexibility can

be given to completely model the general conditional density

function p(y|x), where x is a set of input features and y is

a set of output. The probability density of the target data is

then represented as a linear combination of kernel functions

in the form

p(y|x) =

m=1

(x)φ

(y|x), (1)

where M denotes the total number of mixture components

and the parameter α

(x) denotes the m-th mixing coef-

ﬁcient of the corresponding kernel function φ

(y|x). Al-

though various choices for the kernel function was possible,

for this paper, we utilize the Gaussian kernel of the form

(y|x) = N(y|µ

(x), σ

(x)). (2)

Such formulation is called the Gaussian Mixture Model

(GMM)-based MDN, where a MDN maps input x to the

parameters of the GMM (mixing coefﬁcient α

, mean µ

and variance σ

), which in turn gives a full probability

density function of the output y. It is important to note

that the parameters of the GMM need to satisfy speciﬁc

conditions in order to be valid: the mixing coefﬁcients α

should be positive and sum to 1; the standard deviation σ

should be positive. The use of softmax function and expo-

nential operator in (3) fulﬁlls the aforementioned constraints.

In addition, no extra condition is needed for the mean µ

exp(z

)

i=1

exp(z

)

, σ

= exp(z

), µ

= z

(3)

The parameters z

, z

are the direct outputs of the

MDN corresponding to the mixture weight, variance and

mean for the m-th Gaussian component in the GMM.

308