29.Image Completion with Structure Propagation.pdf

aKun

210

8页

0次

2021-02-23

50墨值下载

Image Completion with Structure Propagation

Jian Sun

Lu Yuan

2∗

Jiaya Jia

3†

Heung-Yeung Shum

Microsoft Research Asia

Tsinghua University

Chinese University of Hong Kong

(a) (b) (c) (d)

Figure 1: Image completion with structure propagation. (a) Input image, (b) unknown region (blue) after removing the pumpkin, with

two intersecting lines (green) speciﬁed by the user, (c) intermediate result after propagating structure and texture information along the

user-speciﬁed lines, and (d) ﬁnal result after ﬁlling in the remaining unknown regions by texture propagation.

Abstract

In this paper, we introduce a novel approach to image com-

pletion, which we call structure propagation. In our system,

the user manually speciﬁes important missing structure in-

formation by extending a few curves or line segments from

the known to the unknown regions. Our approach synthe-

sizes image patches along these user-speciﬁed cu rves in the

unknown region using patches selected around the curves in

the known region. Structure propagation is formulated as

a global optimization problem by enforcing structure and

consistency constraints. If only a single curve is speciﬁed,

structure propagation is solved using Dynamic Program-

ming. When multiple intersecting curves are speciﬁed, we

adopt the Belief Propagation algorithm to ﬁnd the optimal

patches. After completing structure p ropagation, we ﬁll in

the remaining unknown regions using patch-based texture

synthesis. We show that our approach works well on a num-

ber of examples that are challenging to state-of-the-art tech-

niques.

Keywords: Image Completion, Image Inp ainting, Dy-

namic Programming, Belief Propagation, User Interaction

1 Introduction

Image completion, also known as image inpainting, is a chal-

lenging problem in computer graphics and computer vision.

Image completion aims at ﬁ lling in missing pixels in a large

unknown region of an image in a visually plausible way.

Given an input image I with an unknown or missing region

Ω, the goal of image completion is to propagate structure

∗

This work was done when Lu was an intern at MSR Asia.

†

This work was done while visiting MSR Asia.

and texture information from the known or existing regions

I − Ω to Ω, where I is the image region of I. Image com-

pletion is inherently an under-constrained problem.

1.1 Related work

Image inpainting, introduced by Bertalmio et al. [2000], ﬁlls

in holes in an image by propagating image Laplacians in

the isophote direction continuously from the exterior. Their

method is PDE-based and has its root in the Navier-Stokes

equation in ﬂuid dynamics [Bertalmio et al. 2001]. The in-

painting problem has also been formulated in a variational

framework [Ballester et al. 2001]. Chan and Shen [2001]

incorporate Euler’s elastica as a prior to handle curve struc-

tures. Levin et al. [2003] perform image inpainting in the

gradient domain using an image-speciﬁed prior. Im age in-

painting techniques work at the pixel level, and have worked

well for small gaps, thin structures, and text overlays. How-

ever, for larger missing regions or textured regions, they may

generate blurring artifacts.

Example-based approaches [Igehy and Pereira 1997; Harri-

son 2001; Bornard et al. 2002; Barret and Cheney 2002]

have also been proposed for image completion by synthesiz-

ing pix els using texture synthesis techniques [Efros and Le-

ung 1999; Wei and Levoy 2000; Liang et al. 2001; Ashikhmin

2001; Efros and Freeman 2001; Hertzmann et al. 2001].

Recent example-based methods work at the image p atch

level [Drori et al. 2003; Criminisi et al. 2003; Bertalmio et al.

2003; Jia and Tang 2003]. They ﬁll in unknown regions more

eﬀectively by augmenting texture synthesis with some au-

tomatic guidance. This guidance determines the synthesis

ordering, which signiﬁcantly improves the quality of com-

pletion by preserving some salient structures.

For example, a fast smoothing approximation is constructed

in a coarse-to-ﬁne manner to guide an iterative completion

process by adaptive example fragments [Drori et al. 2003].

A conﬁdence map is computed to determine the synthesis

ordering. A priority order is proposed to perform the com-

pletion [Criminisi et al. 2003]. The priority of each patch

is determined from both the conﬁdence map and the image

edges in the patch to encourage propagation of linear struc-

tures. Bertalmio et al. [2003] decompose the input image

into texture and structure components that are completed

using texture synthesis and image inpainting, respectively.

The ﬁnal result is the sum of the two completed components.

Based on texture segmentation, a tensor-voting algorithm is

introduced to smoothly link structures across holes to repair

images [Jia and Tang 2003].

Interactive guidance has also been p roposed. Previous sys-

tems have utilized source region selection, depth informa-

tion [P´erez et al. 2004], and “point of interest” [Drori et al.

2003] to further improve their completion results.

While previous approaches have produced some amazing re-

sults, they have diﬃculties completing images where com-

plex salient structures exist in the missing regions. Such

salient structures may include curves, T-junctions, and X-

junctions. A challenging example to previous techniques is

shown in Figure 1, where the region left by the removed

pumpkin needs to be ﬁlled in. Although the human vi-

sual system has the ability to perceptu ally complete missing

structures [Noe et al. 1998] (e.g., completing the window

frames occluded by the pumpkin in Figure 1), the underly-

ing mechanisms (e.g., visual Gestalt principles [Koﬀka 1935,

1967]) remain unclear. Moreover, previous patch-by-patch

completion algorithms operate in a greedy manner that may

also cause discontinuities in salient stru ctures. Due to the

inherent ambiguity of image completion from a single image,

we must leverage high-level knowledge.

1.2 Our Approach

Our approach is based on the following observations.

• For natu ral images, the most salient missing structures

can often be approximated by a few well-deﬁned curves.

• There exists a synthesis ordering for image completion:

the regions with salient structures should be completed

before ﬁlling in other regions.

Therefore, our approach proceeds in three steps: user inter-

action to specify the curves, structure propagation to syn-

thesize regions with salient structures, and texture propaga-

tion to ﬁll in the remaining unknown regions. Note that we

completely separate structure propagation and texture prop-

agation and perform structure propagation ﬁrst. Compared

with previous methods, this completion process largely re-

duce the breaking of salient structures which human eyes are

sensitive to.

In our system, we allow t he user to draw a few curves that

extend from the known region to the unknown region to in-

dicate how the global structures should be completed. As

shown in Figure 1(b), two nearly perpendicular lines com-

plete the window frames. These two simple lines can sig-

niﬁcantly reduce inherent ambiguity in the unknown regions

because they provide information on what structure should

be propagated and where texture can be obt ained. By draw-

ing a few curves or lines, the user can generate desirable

completed images by propagating the salient structures ac-

cordingly.

Given the user-sp eciﬁed curves, our approach ﬁrst synthe-

sizes t he missing structure and texture information along

the curves inside the unknown region. Unlike previous tech-

niques that synthesize image patches in a greedy patch-

by-patch manner, we formulate structure propagation as a

global optimization problem. For all the patches synthesized

on th e speciﬁed curves, the color diﬀerence in the overlap-

ping area between neighboring patches is globally minimized.

Ω

P (x

)

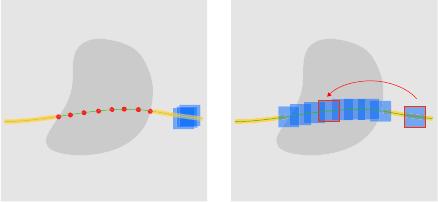
(a) (b)

Figure 2: Structure propagation - 1D chain. (a) I is the

input image region, Ω is the unknown region and C is a user-

speciﬁed curve. St ructure propagation synthesizes missing

image patches on a set of anchor points {p

}

i=1

using the

sample set P. (b) P (x

) is a candidate patch in P which is

chosen for the anchor point p

If a single curve is speciﬁed by the user, we connect the

synthesized patches as a chain, and solve the optimization

problem eﬀectively using dynamic programming. For multi-

ple intersecting curves, we connect the patches as a graph,

and adopt the eﬃcient belief propagation algorithm for op-

timization. Figure 1(c) shows the intermediate result after

structure propagation using belief p ropagation.

The user-speciﬁed curves also partition the input image I

into several regions. Using patch-based texture synthesis,

texture propagation synthesizes the remaining missing re-

gions using samples from respective segmented regions. A

photometric correction method in the gradient domain fur-

ther improves the synthesis results. Figure 1(d) shows the

ﬁnal result after ﬁlling in all unknown regions.

2 Structure Propagation

In this section, we introduce the concept of structure prop-

agation using a single curve C speciﬁed by the user. The

problem we address is how to synthesize missing structure

and texture along curve C in th e unknown region by using

samples around the curve in the known region. Applying

structure propagation for multiple non-intersecting curves is

straightforward. We will discuss the case of multiple inter-

secting curves in Section 3.

We ﬁrst sparsely sample curve C in the unknown region

Ω to generate a set of L anchor points {p

}

i=1

. A s illus-

trated in Figure 2(a), the centers of the synthesized patches

are located at these anchor points, which form a single

chain, or a one-dimensional graph G = {V, E}. V is the

set of L nodes corresponding t o the anchor points, and

E is the set of all edges connecting adjacent no des on C.

The sampling interval is typically half of the patch size to

guarantee suﬃcient overlaps. Outside Ω, the sample set

P = {P (1), P (2), ..., P (N)} contains all patches whose cen-

ters are within a narrow band (typically 1-5 pixels wide)

along curve C, as shown in Figure 2(a). Typically the sam-

ple size N is in the order of hundreds or thousands.

We thus consider structure propagation as a graph labeling

problem. For each anchor position p

, we ﬁnd a label x

∈

{1, 2, ..., N} corresponding t o one of the sample patches. We

select the sample p atch P (x

) from P, and paste it at point

as shown in Figure 2(b).