数据库顶会VLDB 2021最佳EA B论文奖《Are We Ready For Learned Cardinality Estimation》- Xiaoying Wang.pdf

小小亮

748

15页

0次

2021-08-19

免费下载

Are We Ready For Learne d Cardinality Estimation?

Xiaoying Wang

†∗

, Changbo Qu

†∗

, Weiyuan Wu

†∗

, Jiannan Wang

†

, Qingqing Zhou

♦

Simon Fraser University

†

Tencent Inc.

♦

{xiaoying_wang, changboq, youngw, jnwang}@sfu.ca hewanzhou@tencent.com

ABSTRACT

Cardinality estimation is a fundamental but long unresolved prob-

lem in query optimization. Recently, multiple papers from diﬀerent

research groups consistently report that learned models have the

potential to replace existing cardinality estimators. In this paper,

we ask a forward-thinking question: Are we ready to deploy these

learned cardinality models in production? Our study consists of three

main parts. Firstly, we focus on the static environment (i.e., no data

updates) and compare ﬁve new learned methods with nine tradi-

tional methods on four real-world datasets under a uniﬁed workload

setting. The results show that learned models are indeed more ac-

curate than traditional methods, but they often suﬀer from high

training and inference costs. Secondly, we explore whether these

learned models are ready for dynamic environments (i.e., frequent

data updates). We ﬁnd that they cannot catch up with fast data up-

dates and return large errors for diﬀerent reasons. For less frequent

updates, they can perform better but there is no clear winner among

themselves. Thirdly, we take a deeper look into learned models and

explore when they may go wrong. Our results show that the perfor-

mance of learned methods can be greatly aﬀected by the changes

in correlation, skewness, or domain size. More importantly, their

behaviors are much harder to interpret and often unpredictable.

Based on these ﬁndings, we identify two promising research direc-

tions (control the cost of learned models and make learned models

trustworthy) and suggest a number of research opportunities. We

hope that our study can guide researchers and practitioners to work

together to eventually push learned cardinality estimators into real

database systems.

PVLDB Reference Format:

Xiaoying Wang, Changbo Qu, Weiyuan Wu, Jiannan Wang, Qingqing Zhou.

Are We Ready For Learned Cardinality Estimation?. PVLDB, 14(9): 1640 -

1654, 2021.

doi:10.14778/3461535.3461552

PVLDB Artifact Availability:

The source code, data, and/or other artifacts have been made available at

https://github.com/sfu-db/AreCELearnedYet.

1 INTRODUCTION

The rise of “ML for DB” has sparked a large bo dy of exciting research

studies exploring how to replace existing database components with

learned models [

]. Impressive results have been

repeatedly reported from these papers, which suggest that “ML for

DB” is a promising research area for the database community to

This work is licensed under the Creative Commons BY-NC-ND 4.0 International

License. Visit https://creativecommons.org/licenses/by-nc-nd/4.0/ to view a copy of

this license. For any use beyond those covered by this license, obtain permission by

emailing info@vldb.org. Copyright is held by the owner/author(s). Publication rights

licensed to the VLDB Endowment.

Proceedings of the VLDB Endowment, Vol. 14, No. 9 ISSN 2150-8097.

doi:10.14778/3461535.3461552

* The ﬁrst three authors contributed equally to this research.

explore. To maximize the impact of this research area, one natural

question that we should keep asking ourselves is: Are we ready to

deploy these learned models in production?

In this paper, we seek to answer this question for cardinality

estimation. In particular, we focus on single-table cardinality esti-

mation, a fundamental and long standing problem in query opti-

mization [

]. It is the task of estimating the number of tuples

of a table that satisfy the query predicates. Database systems use

a query optimizer to choose an execution plan with the estimated

minimum cost. The performance of a query optimizer largely de-

pends on the quality of cardinality estimation. A query plan based

on a wrongly estimated cardinality can be orders of magnitude

slower than the best plan [42].

Multiple recent papers [

] have shown that learne d

models can greatly improve the cardinality estimation accuracy

compared with traditional methods. However, their experiments

have a number of limitations (see Section 2.5 for more detailed

discussion). Firstly, they do not include all the learned methods in

their evaluation. Secondly, they do not use the same datasets and

workload. Thirdly, they do not extensively test how well learned

methods perform in dynamic environments (e.g., by varying update

rate). Lastly, they mainly fo cus on when learned methods will go

right rather than when they may go wrong.

We overcome these limitations and conduct comprehensive ex-

periments and analyses. The paper makes four contributions:

Are Learned Methods Ready For Static Environments?

propose a uniﬁed workload generator and collect four real-world

benchmark datasets. We compare ﬁve new learned methods with

nine traditional methods using the same datasets and workload in

static environments (i.e., no data updates). The results on accuracy

are quite promising. In terms of training/inference time, there is

only one method [

] that can achieve similar performance with

existing DBMSs. The other learned methods typically require 10

−

1000

more time in training and inference. Moreover, all learned

methods have an extra cost for hyper-parameter tuning.

Are Learned Methods Ready For Dynamic Environments?

We explore how each learned method performs by varying up-

date rate on four real-world datasets. The results show that learned

methods fail to catch up with fast data updates and tend to re-

turn large error for various reasons (e.g., the stale model processes

too many queries, the update period is not long enough to get a

good updated model). When data updates are less frequent, learned

methods can perform better but there is no clear winner among

themselves. We further explore the update time vs. accuracy trade-

oﬀ, and investigate how much GPU can help learned methods in

dynamic environments.

When Do Learned Methods Go Wrong?

We vary correlation,

skewness, and domain size, respectively, on a synthetic dataset, and

try to understand when learned methods may go wrong. We ﬁnd

that all learned methods tend to output larger error on more cor-

related data, but they react diﬀerently w.r.t. skewness and domain

size. Due to the use of black-box models, their wrong behaviors are

1640

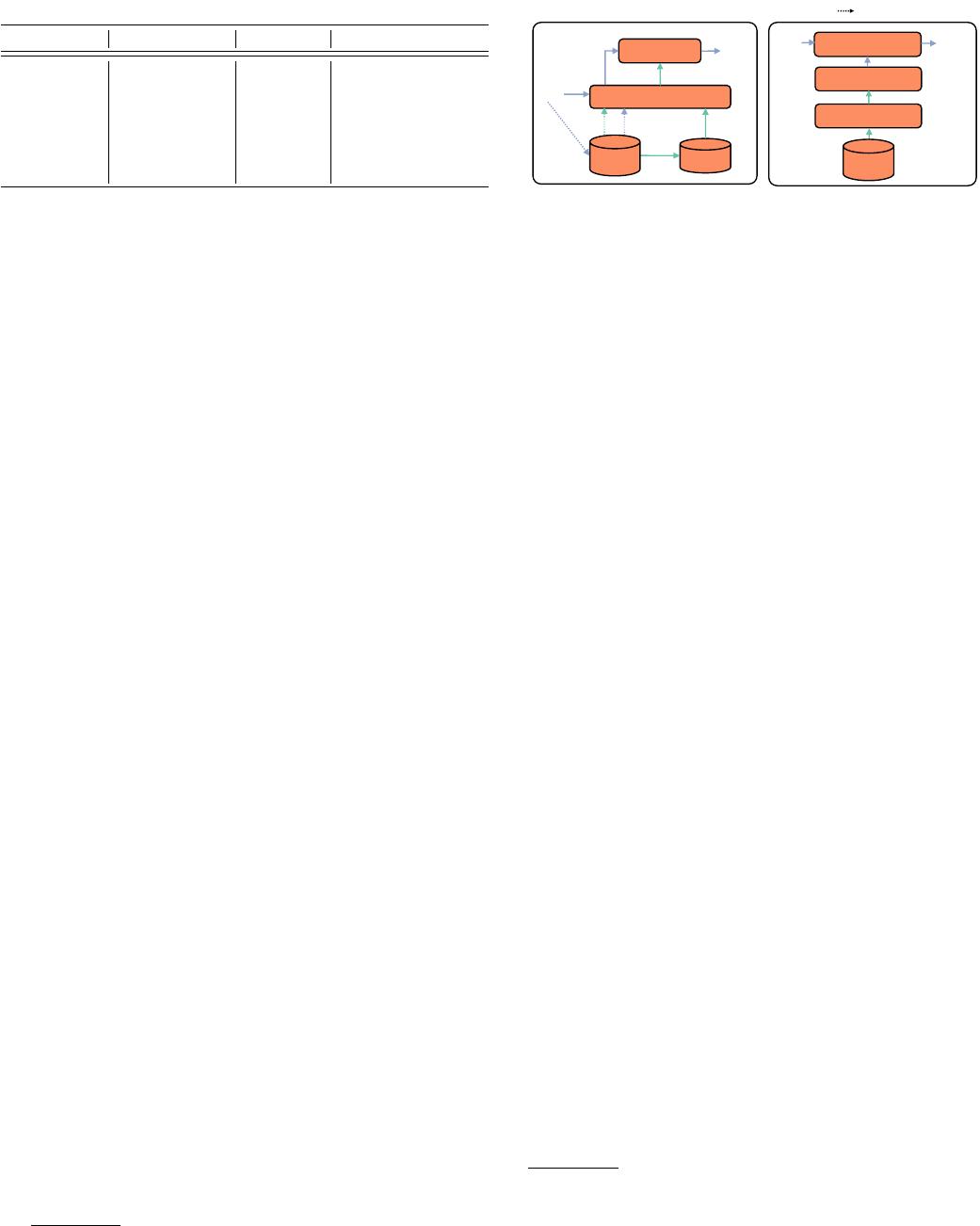
Table 1: Taxonomy of New Learned Cardinality Estimators.

Methodology Input Model

MSCN [34] Regression Query+Data Neural Network

LW-XGB [18]

Regression Query+Data Gradient Boosted Tree

LW-NN [18]

Regression Query+Data Neural Network

DQM-Q [28]

Regression Query Neural Network

Naru [95]

Joint Distribution Data Autoregressive Model

DeepDB [30]

Joint Distribution Data Sum Product Network

DQM-D [28]

Joint Distribution Data Autoregressive Model

very hard to interpret. We further investigate whether their behav-

iors follow some simple and intuitive logical rules. Unfortunately,

most of them violate these rules. We discuss four issues related to

deploying (black-box and illogical) learned models in production.

Research Opportunities.

We identify two future research direc-

tions: i) control the cost of learned methods and ii) make learned

methods trustworthy, and suggest a number of promising research

opportunities. We publish our code and datasets on GitHub

facilitate future research studies. We hope our work can attract

more research eﬀorts in these directions and eventually overcome

the barriers of deploying learned estimators in production.

The rest of the paper is organized as follows: We present a sur-

vey on learned cardinality estimation in Section 2 and describe

the general experimental setup in Section 3. We explore whether

learned methods are ready for static environments in Section 4

and for dynamic environments in Section 5, and examine when

learned methods go wrong in Section 6. Future research opportuni-

ties are discussed in Section 7. Multi-table scenario are discussed

in Section 8 and related works are reviewed in Section 9. Finally,

we present our conclusions in Section 10.

2 LEARNED CARDINALITY ESTIMATION

In this section, we ﬁrst formulate the cardinality estimation (CE)

problem, then put new learned methods into a taxonomy and

present how each method works, and ﬁnally discuss the limita-

tions of existing evaluation on learned methods.

2.1 Problem Statement

Consider a relation



with



attributes

{



,...,



}

and a query

over  with a conjunctive of  predicates:

SELECT COUNT(*) FROM R

WHERE 

AND ··· and 



where





(

 ∈[

,]

) can be an equality predicate like

 = 

, an

open range predicate like

 ≤ 

, or a close range predicate like

 ≤  ≤ 

. The goal of CE is to estimate the answer to this query,

i.e., the number of tuples in



that satisfy the query predicates. An

equivalent problem is called selectivity estimation, which computes

the percentage of tuples that satisfy the query predicates.

2.2 Taxonomy

The idea of using ML for CE is not new (see Section 9 for more

related work). The novelty of recent learned methods is to adopt

more advanced ML models, such as deep neural networks [

], gradient boosted trees [

], sum-product networks [

], and

deep autoregressive models [

]. We call these methods “new

learned methods” or “learned methods” if the context is clear. In

contrast, we refer to “traditional methods” as the methods based on

histogram or classic ML models like KDE and Bayesian Network.

https://github.com/sfu-db/AreCELearnedYet

Data Processing

Query Featurization

Regression Model

Query Pool

+ Labels

Query

Green: Train Stage Blue: Inference Stage

Construct

Train

Result

Statistics

Data

Query Processing

Result

Train

Query

(a) Regression Methods

(b) Joint Distribution Methods

Look Up

Statistics

: Optional

Data

Joint Distribution Model

Figure 1: Workﬂow of Learned Methods.

Table 1 shows a taxonomy of new learned methods

. Based on

the methodology, we split them into two groups - Regression and

Joint Distribution methods. Regression methods (a.k.a query-driven

methods) mo del CE as a regression problem and aim to build a map-

ping between queries and the CE results via feature vectors, i.e.,

𝑦 →  _ → _

. Joint Distribution methods

(a.k.a data-driven methods) model CE as a joint probability distribu-

tion estimation problem and aim to construct the joint distribution

from the table, i.e.,

 (

,

, ··· ,



)

, then estimate the cardinal-

ity. The Input column represents what is the input to construct

each model. Regression metho ds all require queries as input while

joint distribution methods only depend on data. The Model column

indicates which type of model is used correspondingly. We will

introduce these methods in the following.

2.3 Methodology 1: Regression

Workﬂow.

Figure 1(a) depicts the workﬂow of regression methods.

In the training stage, it ﬁrst constructs a query pool and gets the

label (CE result) of each query. Then, it goes through the query

featurization module, which converts each query to a feature vector.

The feature vector does not only contain query information but

also optionally include some statistics (like a small sample) from

the data. Finally, a regression model is trained on a set of

(

feature

vector, label

)

pairs. In the inference stage, given a query, it converts

the query to a feature vector using the same process as the training

stage, and applies the regression model to the feature vector to get

the CE result. To handle data updates, regression methods need to

update the query pool and labels, generate new feature vectors, and

update the regression model.

There are four regression methods: MSCN, LW-XGB, LW-NN,

and DQM-Q. One common design choice in them is the usage

of log-transformation on the selectivity label since the selectivity

often follows a skewed distribution and log-transformation is com-

monly used to handle this issue [

]. These works vary from many

perspectives, such as their input information, query featurization,

and model architecture.

MSCN [34]

introduces a specialized deep neural network model

termed multi-set convolutional network (MSCN). MSCN can sup-

port join cardinality estimation. It represents a query as a feature

vector which contains three modules (i.e., table, join, and predicate

modules). Each module is a two-layer neural network and diﬀerent

module outputs are concatenated and fed into a ﬁnal output net-

work, which is also a two-layer neural network. MSCN enriches the

training data with a materialized sample. A predicate will be evalu-

ated on a sample, and a bitmap, where each bit indicates whether

a tuple in the sample satisﬁes the predicate or not, will be added

Naru, DeepDB and MSCN are named by their authors. For convenience of discussion,

we give others the following short names. Lightweight Gradient Boosting Tree (LW-

XGB) and Lightweight Neural Network (LW-NN) are two models from [

]. From [

two complementary methods are proposed, Data&Query Model - Data (DQM-D) and

Data&Query Model - Query (DQM-Q).

1641

of 15

免费下载

数据库 vldb2021

关注

评论