17-Temporal Network Representation Learning via Historical Neighborhoods Aggregation.pdf

Express

135

12页

0次

2021-11-09

100墨值下载

Temporal Network Representation Learning via

Historical Neighborhoods Aggregation

Shixun Huang

†

Zhifeng Bao

†

Guoliang Li

‡

Yanghao Zhou

†

J. Shane Culpepper

†

RMIT University, Australia

‡

Tsinghua University, China

Abstract—Network embedding is an effective method to learn

low-dimensional representations of nodes, which can be applied

to various real-life applications such as visualization, node clas-

siﬁcation, and link prediction. Although signiﬁcant progress has

been made on this problem in recent years, several important

challenges remain, such as how to properly capture temporal

information in evolving networks. In practice, most networks

are continually evolving. Some networks only add new edges or

nodes such as authorship networks, while others support removal

of nodes or edges such as internet data routing. If patterns exist

in the changes of the network structure, we can better understand

the relationships between nodes and the evolution of the network,

which can be further leveraged to learn node representations

with more meaningful information. In this paper, we propose the

Embedding via Historical Neighborhoods Aggregation (EHNA)

algorithm. More speciﬁcally, we ﬁrst propose a temporal random

walk that can identify relevant nodes in historical neighborhoods

which have impact on edge formations. Then we apply a deep

learning model which uses a custom attention mechanism to in-

duce node embeddings that directly capture temporal information

in the underlying feature representation. We perform extensive

experiments on a range of real-world datasets, and the results

demonstrate the effectiveness of our new approach in the network

reconstruction task and the link prediction task.

I. INTRODUCTION

Network embedding has become a valuable tool for solving

a wide variety of network algorithmic problems in recent years.

The key idea is to learn low-dimensional representations for

nodes in a network. It has been applied in various applications,

such as link prediction [

], network reconstruction [

], node

classiﬁcation [

] and visualization [

]. Existing studies [

] generally learn low-dimensional representations of nodes

over a static network structure by making use of contextual

information such as graph proximity.

However, many real-world networks, such as co-author

networks and social networks, have a wealth of temporal

information (e.g., when edges were formed). Such temporal

information provides important insights into the dynamics of

networks, and can be combined with contextual information in

order to learn more effective and meaningful representations

of nodes. Moreover, many application domains are heavily

reliant on temporal graphs, such as instant messaging networks

and ﬁnancial transaction graphs, where timing information is

critical. The temporal/dynamic nature of social networks has

attracted considerable research attention due to its importance in

many problems, including dynamic personalized pagerank [

advertisement recommendation [

] and temporal inﬂuence

Zhifeng Bao is the corresponding author.

2011

2012

2011

2017

2013

2017

2016

2015

2016

2014

2018

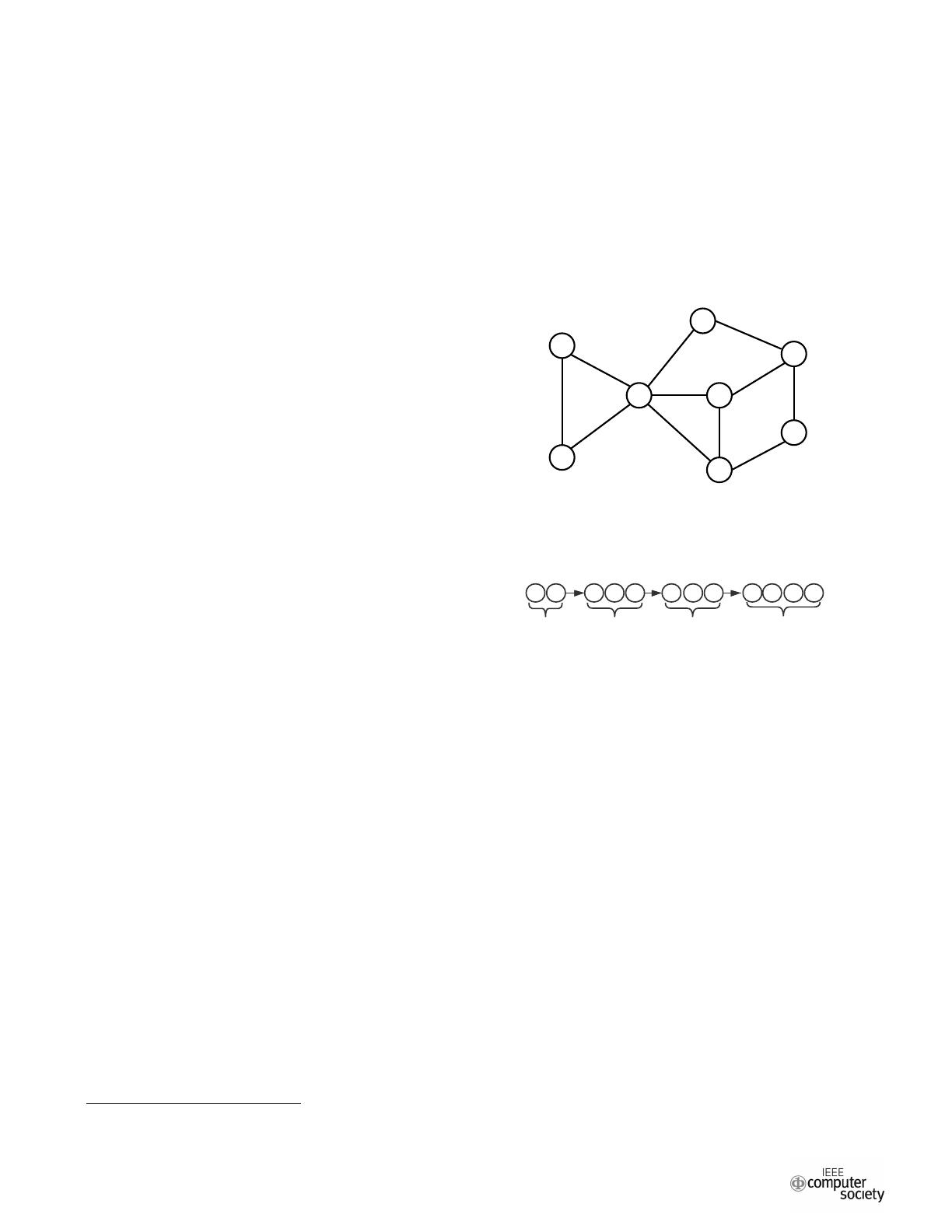
Fig. 1: An example of a co-author temporal network. Each

edge is annotated with a timestamp denoting when the edge

was created.

          

   



Fig. 2: The evolution of a set of nodes that are contextually

and temporally related to node 1.

maximization [

], to name a few. Despite the clear value

of such information, temporal network embeddings are rarely

applied to solve many other important tasks such as network

reconstruction and link prediction [8, 9].

Incorporating temporal information into network embeddings

can improve the effectiveness in capturing relationships between

nodes which can produce performance improvements in down-

stream tasks. To better understand the relationships between

nodes with temporal information in a network, consider Figure 1

which is an ego co-author network for a node (1). Each node

is an author, and edges represent collaborations denoted with

timestamps. Without temporal knowledge, the relationships

between nodes 2, 3, 4, 6 and 7 are indistinguishable since

they are all connected to node 1. However, when viewed from

the temporal perspective, node 1 once was ‘close’ to nodes 2

and 3 but now is ‘closer’ to nodes 4, 6 and 7 as node 1 has

more recent and frequent collaborations with the latter nodes.

Furthermore, in the static case, nodes 2 and 3 appear to be

‘closer’ to node 1 than node 5, since nodes 2 and 3 are direct

neighbors of node 1, whereas node 5 is not directly connected

to node 1. A temporal interpretation suggests that node 5 is also

important to 1 because node 5 could be enabling collaborations

between nodes 1 6, and 7. Thus, with temporal information,

1117

2020 IEEE 36th International Conference on Data Engineering (ICDE)

DOI 10.1109/ICDE48307.2020.00101

Authorized licensed use limited to: Tsinghua University. Downloaded on June 01,2021 at 15:48:53 UTC from IEEE Xplore. Restrictions apply.

new interpretations of the ‘closeness’ of relationships between

node 1 and other nodes and how these relationships evolve are

now possible.

To further develop this intuition, consider the following

concrete example. Suppose node 1 began publishing as a

Ph.D. student. Thus, papers produced during their candidature

were co-authored with a supervisor (node 3) and one of

the supervisor’s collaborators (node 2). After graduation,

the student (node 1) became a research scientist in a new

organization. As a result, a new collaboration with a senior

supervisor (node 4) is formed. Node 1 was introduced to node

5 through collaborations between the senior supervisor (node

4) and node 5, and later began working with node 6 after

the relationship with node 5 was formed. Similarly, after a

collaboration between node 1 and node 6, node 1 met node

7 because of the relationships between node 5 and node 8,

node 8 and node 7, and node 6 and node 7. Hence, as shown

in Figure 2, both the formation of the relationships between

node 1 and other nodes and the levels of closeness of such

relationships evolve as new connections are made between

node 1 and related collaborators.

Thus, the formation of each edge

(x, y)

changes not only the

relationship between

and

but also relationships between

nodes in the surrounding neighborhood. Capturing how and why

a network evolves (through edge formations) can produce better

signals in learned models. Recent studies capture the signal

by periodically probing a network to learn more meaningful

embeddings. These methods model changes in the network by

segmenting updates into ﬁxed time windows, and then learn an

embedding for each network snapshot [

]. The embeddings

of previous snapshots can be used to infer or indicate various

patterns as the graph changes between snapshots. In particular,

CTDNE [

] leveraged temporal information to sample time-

constrained random walks and trained a skip-gram model

such that nodes co-occurring in these random walks produce

similar embeddings. Inspired by the Hawkes process [

] which

shows that the occurrence of current events are inﬂuenced by

the historical events, HTNE [

] leveraged prior neighbor

formation to predict future neighbor formations. In this paper,

we show how to more effectively embed ﬁne-grained temporal

information in all learned feature representations that are

directly inﬂuenced by historical changes in a network.

How to effectively analyze edge formations is a challenging

problem, which requires: (1) identifying relevant nodes (not

limited to direct neighbors) which may impact edge formations;

(2) differentiating the impact of relevant nodes on edge

formations; (3) effectively aggregating useful information from

relevant nodes given a large number of useful but noisy signals

from the graph data.

To mitigate these issues, we propose a deep learning method,

which we refer to as Embedding via Historical Neighborhoods

Aggregation (EHNA), to capture node evolution by probing

the information/factors inﬂuencing temporal behavior (i.e.,

edge formations between nodes). To analyze the formation

of each edge

(x, y)

, we apply the the following techniques.

First, a temporal random walk is used to dynamically identify

relevant nodes from historical neighborhoods that may inﬂuence

new edge formations. Speciﬁcally, our temporal random walk

algorithm models the relevance of nodes using a conﬁgurable

time decay, where nodes with high contextual and temporal

relevance are visited with higher probabilities. Our temporal

random walk algorithm can preserve the breadth-ﬁrst search

(BFS) and depth-ﬁrst search (DFS) characteristics of traditional

solutions, which can then be further exploited to provide both

micro and macro level views of neighborhood structure for

the targeted application. Second, we also introduce a two-level

(node level and walk level) aggregation strategy combined

with stacked LSTMs to effectively extract features from nodes

related to chronological events (when edges are formed). Third,

we propose a temporal attention mechanism to improve the

quality of the temporal feature representations being learned

based on both contextual and temporal relevance of the nodes.

Our main contributions to solve the problem of temporal

network representation learning are:

•

We leverage temporal information to analyze edge forma-

tions such that the learned embeddings can preserve both

structural network information (e.g., the ﬁrst and second

order proximity) as well as network evolution.

•

We present a temporal random walk algorithm which

dynamically captures node relationships from historical

graph neighborhoods.

•

We deploy our temporal random walk algorithm in a

stacked LSTM architecture that is combined with a

two-level temporal attention and aggregation strategy

developed speciﬁcally for graph data, and describe how

to directly tune the temporal effects captured in feature

embeddings learned by the model.

•

We show how to effectively aggregate the resulting

temporal node features into a ﬁxed-sized readout layer

(feature embedding), which can be directly applied to

several important graph problems such as link prediction.

•

We validate the effectiveness of our approach using four

real-world datasets for the network reconstruction and link

prediction tasks.

Organization of this paper.

Related work is surveyed in

Section II and our problem formulation is presented in Sec-

tion III. Next, we describe the problem solution in Section IV.

We empirically validate our new approach in Section V, and

conclude in Section VI.

II. R

ELATED WORK

Static network embedding.

Inspired by classic techniques

for dimensionality reduction [

] and multi-dimensional scal-

ing [

], early methods [

] focused on matrix-

factorization to learn graph embeddings. In these approaches,

node embeddings were learned using a deterministic measure

of graph proximity which can be approximated by computing

the dot product between learned embedding vectors. Methods

such as D

EEP

ALK

[

] and N

ODE

[

] employed a more

ﬂexible, stochastic measure of graph proximity to learn node

embeddings such that nodes co-occurring in short random

1118

Authorized licensed use limited to: Tsinghua University. Downloaded on June 01,2021 at 15:48:53 UTC from IEEE Xplore. Restrictions apply.

of 12

100墨值下载

关注

评论