基于多路径回溯的神经网络验证方法-郑烨，施晓牧，刘嘉祥.pdf

上善若水

645

18页

1次

2022-05-19

免费下载

软件学报 ISSN 1000-9825, CODEN RUXUEW E-mail: jos@iscas.ac.cn

Journal of Software, [doi: 10.13328/j.cnki.jos.006585] http://www.jos.org.cn

基于多路径回溯的神经网络验证方法

∗

郑

烨

施晓牧

刘嘉祥

(深圳大学计算机与软件学院,广东深圳 518060)

通讯作者: 刘嘉祥, E-mail: jiaxiang0924@gmail.com

摘要: 基于线性抽象的符号传播方法在神经网络验证中具有重要地位.针对这类方法,本文提出多路径回溯的

概念.现有方法可看作仅使用单条回溯路径计算每个神经网络节点的上下界,是这一概念的特例.使用多条回溯路径

可以有效改善这类方法的精度.我们在数据集 ACAS Xu, MNIST 和 CIFAR10 上将多路径回溯方法与使用单条回溯

路径的 DeepPoly 进行定量比较,结果表明多路径回溯方法能够获得明显的精度提升,而仅引入较小的额外时间代

价.此外我们在数据集 MNIST 上将多路径回溯方法与使用全局优化的 Optimized LiRPA 比较,结果表明我们的方法

仍然具有精度优势.

关键词: 神经网络验证;符号传播;抽象解释;多路径回溯

中图法分类号: TP311

中文引用格式: 郑烨,施晓牧,刘嘉祥.基于多路径回溯的神经网络验证方法.软件学报. http://www.jos.org.cn/1000-9825/ 6585.htm

英文引用格式: Zheng Y, Liu JX, Shi XM. Multi-path Back-propagation for Neural Network Verification. Ruan Jian Xue Bao/Journal

of Software, 2022 (in Chinese). http://www.jos.org.cn/1000-9825/6585.htm

Multi-path Back-propagation for Neural Network Verification

ZHENG Ye

, SHI Xiao-Mu

, LIU Jia-Xiang

(College of Computer Science and Software Engineering, Shenzhen University, Shenzhen 518060, China)

Abstract: Symbolic propagation methods based on linear abstraction play a significant role in neural network verification. In this paper, we

propose the notion of multi-path back-propagation for these methods. Existing methods are viewed as using only a single back-propagation path

to calculate the upper and lower bounds of each node in a given neural network, being specific instances of our proposed notion. Leveraging

multiple back-propagation paths effectively improves the accuracy of this kind of method. For evaluation, we quantitatively compare our method

using multiple back-propagation paths with the state-of-the-art tool DeepPoly on benchmarks ACAS Xu, MNIST, and CIFAR10. The experiment

results show that our method achieves significant accuracy improvement while introducing only a low extra time cost. In addition, we compare

the multi-path back-propagation method with the Optimized LiRPA, which is based on global optimization, on the dataset MNIST. The results

show that our method still has an accuracy advantage.

Key words: neural network verification; symbolic propagation; abstract interpretation; multi-path back-propagation

神经网络已广泛应用于各种现实场景.过去难以处理的高维复杂问题,如图像分类,神经网络在一定程度上已经

可以达到人类的水平.随着硬件性能提升和算法的进步,神经网络模型甚至在一些问题上已经十分成熟,但同时其可

解释性

[1]

却十分有限.另一方面,由于自身不可避免的过拟合以及攻击技术的发展,使得无论来自于自然或人为影响,

神经网络都是极其不稳定的.因此,在一些安全攸关的应用场景下,神经网络的部署应用存在较强的局限性.比如对

于自动驾驶系统,路标的识别错误可能会导致灾难性的后果.若将神经网络应用于这样的场景,其鲁棒性必须有严格

的保证.

神经网络鲁棒性保障最直接的方法是使用足够多的测试用例来进行测试,但有限的测试用例并不能保证其绝

对安全性.如一张

28 28

像素的灰阶图片,若仅允许对任意像素值最大加

,产生的图片已多达

228 8

种,全部测试显

然不现实.面对这样的问题,神经网络的形式化验证受到了广泛关注,它能够为神经网络的安全性提供数学保证.

神经网络验证要处理的典型问题是网络的可达性质,即给定一个神经网络及输入范围,计算输入范围经过这个

网络能够到达的输出范围.在实际问题中,比如图像分类问题,这一性质通常和局部鲁棒性

[2]

联系在一起.局部鲁棒性

∗ 基金项目:深圳市高等院校稳定支持计划面上项目（项目编号 20200810045225001）；国家自然科学基金青年基金项目（62002228）;

深圳市科创委基础研究面上项目（JCYJ20210324094202008）

收稿时间: 2021-09-05; 修改时间: 2021-10-14; 采用时间: 2022-01-10; jos 在线出版时间: 2022-01-28

Journal of Software

软件学报

是给定一张具体的输入图片和一个最大扰动范围,若扰动后的图片分类标签不发生改变,我们称这个分类网络关于

输入图片和扰动范围是鲁棒的;反之若存在分类标签的改变,则称这个分类网络关于输入图片和扰动范围是不鲁棒

的.这一问题的困难之处在于神经网络中非线性激活函数的叠加,导致难以准确求解网络对输入输出的映射关系.已

经有一些综述

[3-6]

介绍了目前神经网络验证的主流方法和工具,同时能够验证的网络规模也在逐年增加,然而遗憾

的是目前依然没有足够有效的方法能够直接应用于工业场景的问题规模.因此,发展更加快速和准确的神经网络验

证方法备受关注,也是本文的关注点.

本文着重研究只包含 ReLU 激活函数的神经网络.目前对于 ReLU 神经网络的验证方法大致可以分为两类.一

类方法提供可靠(sound)且完备(complete)的结果,即我们不仅能够相信它给出的安全答案,也能够相信它给出的不

安全答案.显然,这要求计算网络在给定输入范围下的准确可达集,文献[7]证明了这类方法具有 NP 时间复杂度.另一

类方法提供可靠却不完备的结果,即能够相信它给出的安全答案,然而当这类方法无法给出答案或给出不安全答案

时,我们无法根据这一结果得到网络不安全的结论.这类方法通常对 ReLU 网络的可达集做上近似处理,即真正的可

达集包含于这类方法计算得到的可达集.因此当这类方法得到的可达集与不安全区域有交集时,并不能说明真正的

可达集与不安全区域有交集.按照近似方法不同,这类方法又可大致分为两组: (1)基于线性抽象,使用线性抽象将

ReLU 激活函数抽象为包含其凸包的线性约束区域

[8,9]

; (2)基于半正定规划(SDP),将 ReLU 激活函数表示为二次约

束,再将得到的验证问题松弛为 SDP 问题

[10,11]

.上近似方法相较于计算准确可达集有较低的时间复杂度.尤其是线性

抽象方法,它使用容易求解的线性形式近似网络的真正可达集,能够用于验证较大规模的网络.

与线性抽象紧密相关的另一个概念是符号传播

[12]

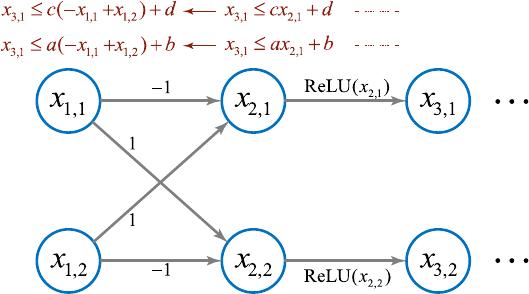
.符号传播技术在神经网络上传播节点取值的符号约束.如在

图 1 中, 节点

2,1

的取值依赖

1,1

和

1,2

,它们的关系是

2,1 11 1,2

xxx+= −

;而

3,1

的取值依赖

2,1

,它们的关系是

3,1 2,1

ReLU( )xx =

.则代入

2,1

的符号约束,可得

3,1 1,1 1,2

ReLU( )x xx+

= −

.符号传播可以用来显式地描述节点之间的取

值关系,是一种有效分析神经网络的方法.线性抽象则是将上述非线性的关系式

3,1 1,1 1,2

ReLU( )x xx+= −

抽象为线性

约束,以降低求解难度.

针对基于线性抽象的符号传播方法,本文提出多路径回溯的概念.例如在图 1 中,若节点值

3,1 2,1

ReLU( )xx =

被抽

象为区间

2,1

[0, ]

ax b

,其中

,ab

为确定常数,那么

3,1

的上界可由

3,1 2,1

x ax b≤+

确定.利用

2,1

的符号约束向输入层替

换,可得到此上界关于输入层的表示

3,1 1,1 1,2

()x ax x b≤− + +

.利用符号约束替换到输入层的符号传播过程实际上确

定了

3,1

上界的一条传播路径,我们称之为回溯路径(back-propagation path),这类方法的代表是 DeepPoly

[13]

.若

3,1

有

另一上界

3,1 2,1

x cx d≤+

,则上述替换过程可确定

3,1

上界的另一条回溯路径,进而得到

3,1

的另一个上界表示.在多路

径回溯的概念下,已有的方法仅使用单条回溯路径,因此只能得到

3,1

的一个上界.使用多条回溯路径可以得到

3,1

的多个上界,从而可能得到比使用单条回溯路径更为精确的上界.更精确的上下界是这类方法的关键,它有助于得到

更精确的验证结果.

回溯路径 1

回溯路径 2

Fig.1 Two back-propagation paths of node x

3,1

图 1 节点 x

3,1

的两条回溯路径

本文对基于线性抽象的符号传播方法作出改进,旨在提高这类方法的精度.我们的主要贡献有以下三点:

 我们提出了多路径回溯的概念,并指出现有的基于线性抽象的符号传播方法仅使用单条回溯路径计算神

经网络节点上下界,是多路径回溯的一种特例.

 我们实现了多路径回溯方法,并在数据集 ACAS Xu, MNIST 及 CIFAR10 上与使用单条回溯路径的

DeepPoly 对比.结果表明,使用多条回溯路径能够明显提升验证精度,而仅引入较低的额外时间代价.

of 18

免费下载

软件学报计算机技术

关注

评论