2022SIGMOD论文_LevelIndex Towards Efficient Query Processing in Continuous Preference Space.pdf

Bigbig

14页

1次

2022-07-20

免费下载

𝜏-LevelIndex: Towards Eicient ery Processing in

Continuous Preference Space

Jiahao Zhang

†

, Bo Tang

‡§

, Man Lung Yiu

†

, Xiao Yan

‡§

, Keming Li

‡§ ∗

†

Department of Computing, Hong Kong Polytechnic University

Research Institute of Trustworthy Autonomous Systems, Southern University of Science and Technology

‡

Department of Computer Science and Engineering, Southern University of Science and Technology

{csjhzhang,csmlyiu}@comp.polyu.edu.hk,{tangb3@,yanx@,likm2020@mail.}sustech.edu.cn

ABSTRACT

Top-

𝑘

related queries in continuous preference space (e.g., k-shortlist

preference query

kSPR

, uncertain top-

𝑘

query

UTK

, output-size

specied utility-based query

ORU

) have numerous applications but

are expensive to process. Existing algorithms process each query via

specialized optimizations, which are dicult to generalize. In this

work, we propose a novel and general index structure

𝜏

LevelIndex

which can be used to process various queries in continuous pref-

erence space eciently. We devise ecient approaches to build

the

𝜏

LevelIndex

by fully exploiting the properties of continuous

preference space. We conduct extensive experimental studies on

both real- and synthetic- benchmarks. The results show that (i)

our proposed index building approaches have low costs in terms

of both space and time, and (ii)

𝜏

LevelIndex

signicantly outper-

forms specialized solutions for processing a spectrum of queries in

continuous preference space, and the speedup can be two to three

orders of magnitude.

CCS CONCEPTS

• Information systems → Top-k retrieval in databases.

KEYWORDS

k-level index, preference space, top-𝑘 query processing

ACM Reference Format:

Jiahao Zhang, Bo Tang, Man Lung Yiu, Xiao Yan, Keming Li. 2022.

𝜏

LevelIndex: Towards Ecient Query Processing in Continuous Preference

Space. In Proceedings of the 2022 International Conference on Management

of Data (SIGMOD’22), June 12–17, 2022, Philadelphia, PA, USA. ACM, New

York, NY, USA, 14 pages. https://doi.org/10.1145/3514221.3526182

1 INTRODUCTION

The preference model is widely used in many applications, e.g.,

recommender system, multi-criteria decision making, and prod-

uct ranking. Specically, each option in the market has several

∗

Dr. Bo Tang is the corresponding author.

Permission to make digital or hard copies of all or part of this work for personal or

classroom use is granted without fee provided that copies are not made or distributed

for prot or commercial advantage and that copies bear this notice and the full citation

on the rst page. Copyrights for components of this work owned by others than ACM

must be honored. Abstracting with credit is permitted. To copy otherwise, or republish,

to post on servers or to redistribute to lists, requires prior specic permission and/or a

fee. Request permissions from permissions@acm.org.

SIGMOD’22, June 12–17, 2022, Philadelphia, PA, USA.

ACM ISBN 978-1-4503-9249-5/22/06.. . $15.00

https://doi.org/10.1145/3514221.3526182

attributes and the value of each attribute models the competitive-

ness of the option. For example, each hotel in the online portals

(e.g, Booking [

] and TripAdvisor [

]) includes value, facility, and

cleanliness attributes. The attribute values of Crowne Plaza Hotel

in Booking are 0.83, 0.86, 0.89, respectively. We denote an option

with

𝑑

attributes as r

= (𝑟 [

], 𝑟 [

], · · · , 𝑟 [𝑑])

and all options form

the dataset

. A user chooses options based on her preference

weight vector w

= (𝑤 [

], 𝑤 [

], · · · , 𝑤 [𝑑])

, which species a nu-

meric weight for each attribute. To compute the score of each option

for the user, a linear scoring function (i.e.,

(

) =

𝑑

𝑖=1

𝑟 [𝑖]𝑤 [𝑖]

)

is used and the top-

𝑘

products with the highest scores are appeal-

ing to the user. In the past decades, the database community has

conducted extensive studies on shortlisting product options for

users, i.e., top-

𝑘

query [

], skyline query [

], and hybrids

of top-

𝑘

and skyline queries [

Rtree

and its variants [

]

are widely used to accelerate the above query processing.

Besides nding top-

𝑘

options for users, it is also important to

consider user preferences from the perspective of product providers.

For instance, a hotel manager may want to identify potential cus-

tomers who rank his hotel as top-

𝑘

, which should be targeted in

advertising campaigns. Recently, many queries (e.g., Monochromatic

reverse top-

𝑘

[

MaxRank

[

kSPR

[

], restricted skyline [

UTK

[

], and

ORU

[

]) are proposed to explore the entire user

preference space (i.e., the continuous space dened by preference

weight w) instead of discrete user preference weights in traditional

top-

𝑘

ranking queries (i.e., points in the preference space). These

queries can help product providers analyze the competitiveness of

their products in the market, identify target users, adjust the design

of products to attract more users, etc. For example, the

MaxRank

query [

] reports the maximum rank a product can have among

all possible users’ preferences, which tells the product provider the

market status of his product.

Many algorithms have been proposed to accelerate the query

processing in continuous preference space, but they are still inade-

quate in two aspects. First, the query processing complexity is high

even with state-of-the-art solutions as many expensive geometric

operations are involved. For example, our experiments show that

an ORU query can take more than 1000 seconds. Second, Existing

algorithms develop specialized techniques for each query and there

lacks a general index structure that accelerates a wide range of

queries in continuous preference space, i.e., an analogue of

Rtree

for top-𝑘 ranking queries.

In this work, we devise a general index (

𝜏

LevelIndex

) for queries

in continuous preference space, where

𝜏

is a user-specied param-

eter. A general index is favorable as it not only reduces query

Session 28: Spatial, Temporal, and Multimedia Databases

SIGMOD ’22, June 12–17, 2022, Philadelphia, PA, USA

2149

processing complexity by avoiding expensive geometric operations

but also amortizes the index construction and storage costs among

queries (either of the same or dierent types).

Specically, each option r in the dataset corresponds to a hy-

perplane

(

)

in continuous preference space, and the cell in

𝜏

LevelIndex

is dened by a set of halfspaces, which is formed

by option hyperplanes. As we will elaborate in Section 4, many

queries in continuous preference space can be processed by nd-

ing some cells in

𝜏

LevelIndex

or the options associated with cer-

tain cells. Constructing

𝜏

LevelIndex

can be converted to the fa-

mous

𝜏-𝑙𝑒𝑣𝑒𝑙

problem [

] in computational geometry. However, the

𝜏-𝑙𝑒𝑣𝑒𝑙

problem is only solved theoretically with time complexity

𝑂 (𝑛

⌊

𝑑

⌋

𝜏

⌈

𝑑

⌉

)

[

], where

𝑛

is the number of options in the dataset

, and

𝑑

is the dimensionality of each option. The challenges of de-

signing an eective index structure and ecient building procedure

for 𝜏-LevelIndex are:

•

Generality and query eciency. There are many types of

queries in continuous preference space, e.g.,

kSPR

UTK

ORU

How to design the structure of

𝜏

LevelIndex

such that it can support

all these queries and process them eciently?

•

Index size. As proved in [

], the total number of cells at level

ℓ ∈

[

, 𝜏]

𝜏

LevelIndex

𝑂 (𝑛

⌊

𝑑

⌋

ℓ

⌈

𝑑

⌉

)

, and each cell is dened

by the intersection of a set of halfspaces. Thus,

𝜏

LevelIndex

will

be overwhelmingly large if cells are expressed explicitly. How to

dene cells and arrange them in

𝜏

LevelIndex

to make the index

size practical?

•

Index building time. Using [

] to build

𝜏

LevelIndex

has time

complexity

𝑂 (𝑛

⌊

𝑑

⌋

𝜏

⌈

𝑑

⌉

)

. Moreover, computing the cells in

𝜏

LevelIndex

requires expensive computational geometric opera-

tions (e.g.,

Intersect

and

Containment

). How to build

𝜏

LevelIndex

eciently with a reasonable time cost?

To overcome the above challenges, we rst dene the basic unit

𝜏

LevelIndex

(i.e., cell) in a compact manner by implicitly ex-

ploiting its geometric properties, and connect two cells in adjacent

levels of

𝜏

LevelIndex

if they have a parent-child relation. This struc-

ture not only reduces the index size but also enables

𝜏

LevelIndex

to process many queries (if not all) eciently, as usually only a

small number of cells need to be visited. We then propose three

approaches (i.e., the

UTK

-adapted approach BSL, the insertion-

based approach

IBA

and the partition-based approach

PBA

) to build

𝜏

LevelIndex

. BSL and

IBA

are simple but inecient. However, they

provide insights (i.e., avoid redundant halfspaces in cells and reduce

unnecessary cell insertion checking) to devise novel and ecient

PBA

. We further utilize the dominance relations among options to

improve the performance of PBA.

To the best of our knowledge, this is the rst work in the database

community that proposes a general index for a spectrum of queries

in continuous preference space. Moreover, this work also proposes

the rst practical solution to the well-known

𝜏-𝑙𝑒𝑣𝑒𝑙

problem (i.e.,

building

𝜏

LevelIndex

) in the computational geometry community.

In addition to answering continuous preference space queries in

database community,

𝜏

LevelIndex

may also nd applications in

computational geometry, e.g., simplex range searching [

], Voronoi

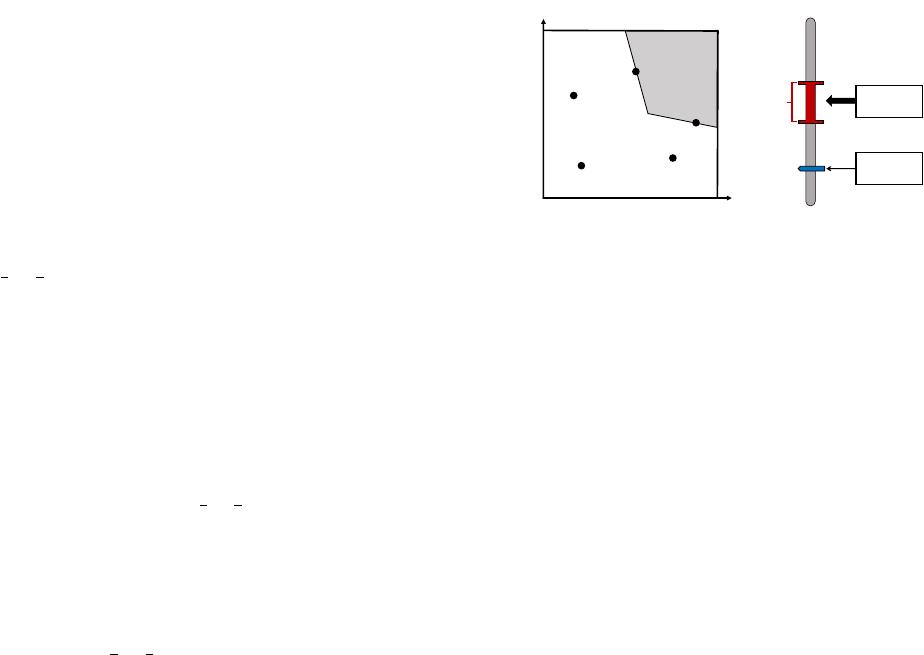
Yotel

(0.26,0.64)

VibesInn

(0.62,0.76)

Artezen

(0.90,0.48)

citizenM

(0.73,0.33)

service (𝑟[2])

value (𝑟[1])

𝑜𝑅

Royalton

(0.30,0.24)

Artezen

VibesInn

𝑤[1]

top-2 hotels

VibesInn

Yotel

0.60

0.40

0.18

(a) Product space (b) Preference space

Figure 1: Discrete and continuous space

diagram computing [

], graph drawing [

]. To sum up, the tech-

nical contributions of our work are as follows:

•

We design a succinct structure for

𝜏

LevelIndex

with a novel

implicit cell representation and formally dene the

𝜏

LevelIndex

building problem in Section 3.

•

For three representative queries (i.e.,

kSPR

UTK

, and

ORU

) in

continuous preference space, we show how to use

𝜏

LevelIndex

to process them eciently in Section 4.

•

We propose three building approaches for

𝜏

LevelIndex

with a

suite of optimization techniques, which have low costs in both

space and time, in Sections 5 and 6.

•

We conduct extensive experiments on both synthetic- and real-

datasets to validate the eciency of our proposals for

𝜏

LevelIndex

building problem. Moreover, for three representative queries, we

demonstrate the advantage of

𝜏

LevelIndex

in query processing

eciency over their state-of-the-art solutions in Section 7.

The remainder of this paper is organized as follows. Section 2

presents the preliminary and reviews the related work. Section 3

illustrates the

𝜏

LevelIndex

building problem. Section 4 shows how

to process three representative queries via

𝜏

LevelIndex

. Sections 5

and 6 present our devised approaches for

𝜏

LevelIndex

building.

Section 7 evaluates the eectiveness of our proposals by extensive

experiments, and Section 8 concludes this work.

2 PRELIMINARY AND RELATED WORK

In this part, we introduce the preliminary of ranking queries in

Section 2.1, then discuss the related work in Section 2.2.

2.1 Preliminary

Ranking queries have been extensively studied in the database

community. Usually, it ranks products in the market by the users’

preferences. Consider the option dataset

D = {

, · · · ,

𝑛

}

product space, it contains

𝑛

options, which correspond to prod-

ucts such as hotels, laptops or phones in the market. Each product

option r

= (𝑟 [

], 𝑟 [

], · · · , 𝑟 [𝑑]) ∈ D

is a discrete point in the

𝑑

dimensional option space

𝑑

, see discrete black points in Figure 1(a),

in which each dimension models an attribute of the product. The

hotel dataset in Figure 1(a) has 5 hotels, each has two attributes

value

(𝑟 [

])

and service

(𝑟 [

])

. For example, the attributes value and

service of Artezen are 0.90 and 0.48, respectively. The gray area in

Figure 1(a) shows a continuous region

𝑜𝑅

in product space, we will

elaborate it shortly. A user’s preference for the attributes is captured

Session 28: Spatial, Temporal, and Multimedia Databases

SIGMOD ’22, June 12–17, 2022, Philadelphia, PA, USA

2150

of 14

免费下载

关注

评论