SupercheQ：Quantum Advantage for Distributed Databases_P. Gokhale.pdf

通讯员

116

16页

1次

2022-12-09

免费下载

SupercheQ: Quantum Advantage for Distributed Databases

P. Gokhale,

1, ∗

E. R. Anschuetz,

1, 2, ∗

C. Campbell,

F. T. Chong,

1, 4

E. D. Dahl,

Frederick,

E. B. Jones,

B. Hall,

S. Issa,

P. Goiporia,

S. Lee,

P. Noell,

V. Omole,

Owusu-Antwi,

M. A. Perlin,

R. Rines,

M. Saﬀman,

3, 5

K. N. Smith,

and T. Tomesh

1, 6

Super.tech, a division of Inﬂeqtion

Department of Physics, Massachusetts Institute of Technology

ColdQuanta, a division of Inﬂeqtion

Department of Computer Science, University of Chicago

Department of Physics, University of Wisconsin-Madison

Department of Computer Science, Princeton University

(Dated: December 8, 2022)

We introduce SupercheQ, a family of quantum protocols that achieves asymptotic advantage over

classical protocols for checking the equivalence of ﬁles, a task also known as ﬁngerprinting. The

ﬁrst variant, SupercheQ-EE (Eﬃcient Encoding), uses n qubits to verify ﬁles with 2

O(n)

bits—

an exponential advantage in communication complexity (i.e. bandwidth, often the limiting factor in

networked applications) over the best possible classical protocol in the simultaneous message passing

setting. Moreover, SupercheQ-EE can be gracefully scaled down for implementation on circuits with

poly(n

) depth to enable veriﬁcation for ﬁles with O(n

) bits for arbitrary constant `. The quantum

advantage is achieved by random circuit sampling, thereby endowing circuits from recent quantum

supremacy and quantum volume experiments with a practical application. We validate SupercheQ-

EE’s performance at scale through GPU simulation. The second variant, SupercheQ-IE (Incremental

Encoding), uses n qubits to verify ﬁles with O(n

) bits while supporting constant-time incremental

updates to the ﬁngerprint. Moreover, SupercheQ-IE only requires Cliﬀord gates, ensuring relatively

modest overheads for error-corrected implementation. We experimentally demonstrate proof-of-

concepts through Qiskit Runtime on IBM quantum hardware. We envision SupercheQ could be

deployed in distributed data settings, accompanying replicas of important databases.

I. INTRODUCTION

A hallmark of modern networks and databases is dis-

tributed replication of ﬁles, whether to improve availabil-

ity, redundancy, or performance. However, replication

requires protocols for integrity veriﬁcation to check that

copies of data have not diverged. This motivates the

task of ﬁngerprinting: mapping an input bitstring to a

shorter bitstring (the ﬁngerprint) in order to distinguish

two inputs with (arbitrarily) high success probability.

Fingerprinting has been extensively studied in the so-

called simultaneous message passing (SMP) setting [1–3].

In this model, ﬁngerprints of two bitstrings A and B are

sent to a referee to verify whether A = B with high prob-

ability. The goal is to minimize the communication com-

plexity, i.e. the number of bits transferred to the referee,

of this process. Previous work [4] has shown that there

is an exponential advantage in communication complex-

ity when utilizing quantum states for this task. Namely,

for A and B each of N bits, there is a quantum proto-

col that succeeds with high probability using O (log N)

qubits, while there is a known achievable lower-bound of



√



classical bits in performing this task [2]. Un-

fortunately, the protocol of [4] requires constructing a

complicated superposition state that generally takes time

scaling with N to prepare on a quantum computer.

∗

These two authors contributed equally

SupercheQ–EE

SupercheQ–IE

101110010…

Alice

(N bits)

101110010…

Random circuit sampling

𝑂(log 𝑁) qubits transmitted.

𝑂(𝑁

!/#

)

with

poly(𝑘)

cost.

Bob

(N bits)

101110010…

Graph state encoding with O(1) incremental updates

𝑂( 𝑁) qubits transmitted.

QPU

01110010…

QPU

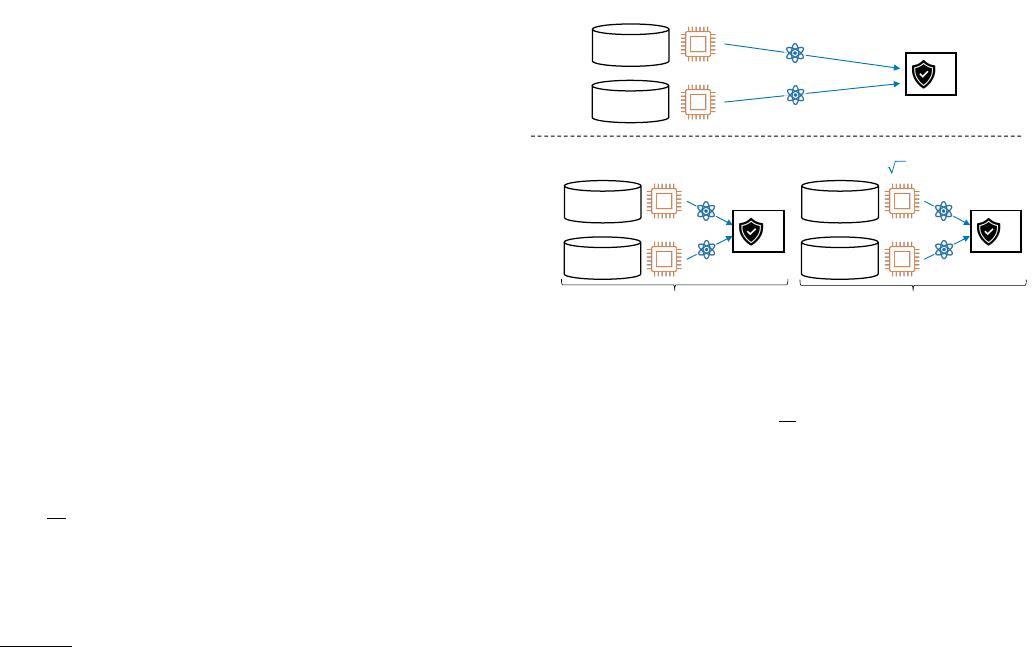
FIG. 1. The EE (Eﬃcient Encoding) variant of SupercheQ

compares two N-bit ﬁles by transmitting as few as O(log N)

qubits—an exponential advantage over classical protocols in

the SMP setting. The IE (Incremental Encoding) variant

matches the best-possible Θ(

√

N) scaling of classical proto-

cols while achieving constant-time updates for incremental ﬁle

changes.

To address these diﬃculties we introduce SupercheQ,

a family of quantum protocols that exhibit asymp-

totic advantage over classical protocols for ﬁngerprint-

ing, as summarized in Fig. 1 and Table I. The ﬁrst

variant, SupercheQ-EE (Eﬃcient Encoding), achieves an

advantage in communication complexity. This is of-

ten the limiting factor for modern distributed databases.

arXiv:2212.03850v1 [quant-ph] 7 Dec 2022

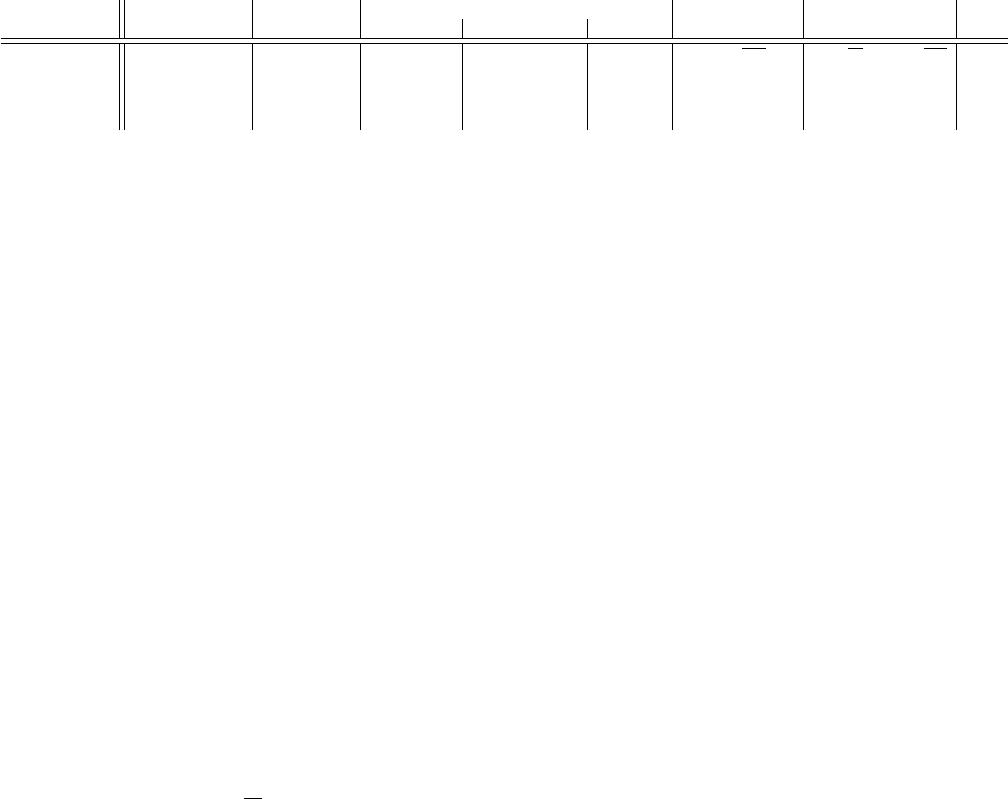
Protocol Hash Quantum FP SupercheQ-EE [§III A, III B, III C] SupercheQ-IE Classical FP Naive

[Example] [SHA-256] [4] [Haar Rdm] [Aprx t-Dsgn] [HW-Eﬀ] [§IV] [3]

FP Size (n) O(1), [256 bits] O(log N ) O(log N ) O(N

1/`

) Empirical

∼

√



√



∼

√

Quantum Cost N/A exp(n) exp(n) poly(n

) Empirical O(N ) N/A N/A

Collision-Free? No Yes Yes Yes Yes Yes Yes Yes

Incremental? ?, [No] No No No No Yes No Yes

TABLE I. Comparison of ﬁngerprinting (FP) protocols for ﬁles with N classical bits, in ascending order of the ﬁngerprint size.

Quantum cost refers to the gate count needed to produce the quantum ﬁngerprint state. Collision-free refers to whether the

protocol is with high probability safe against worst-case choices of ﬁles; in particular, hashing to a constant size (e.g. SHA-256)

is not collision-free because there always exist (many) pairs of ﬁles that map to the same hashed value. Incremental refers to

whether ﬁngerprints can be updated in constant time when the underlying ﬁle is bit-ﬂipped. We introduce SupercheQ-Eﬃcient

Encoding (EE), which encompasses three subcategories: Haar-Random (§III A), Approximate Unitary t-Design (§III B), and

Hardware-Eﬃcient variant (§III C). We also introduce SupercheQ-Incremental Encoding (IE), which is the only protocol here

that achieves incremental updates.

SupercheQ-EE can be used to check if two 2

O(n)

-bit ﬁles

are identical by sending only n qubits, which is an expo-

nential advantage relative to the best-possible classical

protocol. In a nearer-term setting with restricted quan-

tum circuit gate counts and connectivity, SupercheQ-

EE can compare ﬁles of size O(n

) bits for arbitrarily

large constant `, with quantum circuit cost that scales

as poly(n

). For comparison, ` = 2 is known to be the

best that can be achieved classically in the SMP set-

ting [2, 5]. Interestingly, SupercheQ-EE’s core mecha-

nism is random circuit sampling. As such, SupercheQ-EE

endows circuits from quantum supremacy and quantum

volume experiments with the ﬁrst plausible application

to our knowledge, though current noise rates do not yet

permit a practical advantage.

The second variant, SupercheQ-IE (Incremental En-

coding), matches the ` = 2 quadratic scaling of the best

possible classical protocol, but with the advantage of be-

ing incremental. Speciﬁcally, if a bit is ﬂipped in an N-

bit source ﬁle, the n = Θ(

√

N)-qubit ﬁngerprint can be

updated in constant time. To our knowledge, no nontriv-

ial classical ﬁngerprinting protocols guarantee this prop-

erty, nor are they likely to achieve this property. The

SupercheQ-IE protocol has two somewhat counterintu-

itive features:

1. The essential ingredient is a Cliﬀord circuit, which

is known to be eﬃciently classically simulable with

a quadratic memory overhead. However, this

quadratic separation is known to be optimal [6–8]

(i.e. it takes quadratically more classical bits than

qubits to simulate Cliﬀord circuits). As a result,

quantum advantages are known to still persist in

a variety of communication complexity settings, as

recently demonstrated by [7, 8].

2. The protocol does not involve Grover search and

no quantum random access memory (QRAM) is

involved—only an ordinary classical database.

These features are appealing for error-corrected imple-

mentations of SupercheQ-IE. Since only Cliﬀord circuits

are required, SupercheQ-IE avoids the overhead of magic

state distillation for non-Cliﬀord operations [9]. More-

over, no special hardware for classical data loading is

required.

The remainder of this paper is organized as follows.

Sec. II provides background on ﬁngerprinting for check-

ing equivalence of data. Secs. III and IV specify the

SupercheQ-EE (Eﬃcient Encoding) and SupercheQ-IE

(Incremental Encoding) protocols, respectively. Since

our asymptotic bounds for SupercheQ-EE are loose,

we employ GPU-accelerated simulation to elucidate

the real-world advantage achievable with SupercheQ in

Sec. V. Next, we demonstrate experimental results for

SupercheQ, executed on IBM quantum hardware, in

Sec. VI. Finally, we conclude in Sec. VII. Appendix A

presents mathematical proofs for key results, and Ap-

pendix B contains additional plots pertaining to noisy

simulation of SupercheQ-EE.

II. BACKGROUND

A. Notation and Setup

Throughout this paper, N will denote the number of

classical bits composing a ﬁle of interest, while n will de-

note the number of qubits in the ﬁngerprint. We focus

exclusively on the simultaneous message passing (SMP)

setting [1]. Under this model, we consider the communi-

cation complexity for Alice and Bob to send the ﬁnger-

print to a third-party referee, as depicted in Fig. 1. The

SMP setting allows for both Alice and Bob to have pri-

vate coins (i.e., uncorrelated randomness), but assumes

that Alice and Bob do not share a secure random key

(which would require a secure key exchange protocol).

B. Fingerprinting

The most naive classical procedure for ﬁngerprinting a

ﬁle is to send the entire ﬁle itself. In this case—which cor-

responds to the right-most column in Table I—we have

that n = N . On the other end of the spectrum, we may

of 16

免费下载

quantum 量子数据库

关注

评论