




Time Series Data Cleaning From Anomaly Detection To Anomaly Repairing.pdf
免费下载
Time Series Data Cleaning: From Anomaly Detection to
Anomaly Repairing
Aoqian Zhang
School of Software,
Tsinghua University
zaq13@mails.tsinghua.edu.cn
Shaoxu Song
School of Software,
Tsinghua University
sxsong@tsinghua.edu.cn
Jianmin Wang
School of Software,
Tsinghua University
jimwang@tsinghua.edu.cn
Philip S. Yu
University of Illinois at Chicago
Institute for Data Science,
Tsinghua University
psyu@cs.uic.edu
ABSTRACT
Errors are prevalent in time series data, such as GPS t rajec-
tories or sensor readings. Existing methods focus more on
anomaly detection but not on repairing the detected anoma-
lies. By simply filtering out the dirty data via anomaly
detection, applications could still be unreliable over the in-
complete time series. Instead of simply discarding anoma-
lies, we propose to (iteratively) repair them in time series
data, by creatively bond in g the beauty of temporal n ature
in anomaly detection with the widely considered minimum
change principle in data repairing. Our major contributions
include: (1) a novel framework of iterative minimum re-
pairing (IMR) over time series data, (2) explicit analysis on
convergence of the prop osed iterative min imum repairing,
and (3) efficient estimation of parameters in each iteration.
Remarkably, with incremental computation, we reduce the
complexity of parameter estimation from O(n) to O(1). Ex-
periments on real datasets demonstrate the superiority of
our proposal compared to the state-of-the-art approaches.
In particular, we show that (the proposed) repairing indeed
improves the time series classification application.
1. INTRODUCTION
Time series data are often found with dirty or imp recise
values, such as GPS trajectories, sensor reading sequences
[15], or even stock prices [16]. For example, the price of
SALVEPAR (SY) is misused as the price of SYBASE (SY),
both of which share the same notation (SY) in some sources.
It is different from the interesting anomaly that actually
happens in real life, e.g., the temperatures sudden change
from 20C to 10C in on e day when cold air rushes in. To
distinguish such cases, we propose to employ some labeled
This work is licensed under the Creative Commons Attribution-
NonCommercial-NoDerivatives 4.0 International License. To view a copy
of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. For
any use beyond those covered by this license, obtain permission by emailing
info@vldb.org.
Proceedings of the VLDB Endowment, Vol. 10, No. 10
Copyright 2017 VLDB Endowment 2150-8097/17/06.
truth of dirty observations. (See more detailed examples on
dirty data and their labeled truth in Example 1.)
1.1 Motivation on Anomaly Repairing
Applications, such as pattern mining [17] or classification
[26], built upon the dirty time series data are obviously not
reliable. Anomaly detection over time series is often applied
to filter out the dirty data (see [11] for a comprehensive and
structured overview of anomaly detection techniques). That
is, the detected anomaly data points are simply discarded
as useless noises. Unfortunately, with a large number of
consecutive data points eliminated, t he applications could
be barely performed over the rather incomplete time series.
Recent study [21] shows that repairing dirty values could
improve clustering over spatial data. For time series data,
we argue that repairing the anomaly can also improve the
applications such as time series classification [26]. A repair
close to the truth helps greatly the applications.
1.2 Potential Methods for Repairing
A straightforward idea is to directly interpret the predi-
cation values in anomaly detection, e.g., by AR [3, 14, 27]
or ARX [3, 19], as repairs (see details in Section 2). A d ata
point is considered as anomaly if its (tru th) predication sig-
nificantly differs from (noisy) observation. Unfortunately,
noisy/erroneous data are often close to the truth in prac-
tice, under the intuition that human or systems always try to
minimize their mistakes, e.g., misspellings (John Smith vs.
Jhon Smith), typos (555-8145 vs. 555-8195) as illustrated in
[1], rounding off (76,821,000 vs. 76M) or unit error ( 76M vs.
76B) as shown in [16]. Owing to such disagreement, the re-
pairing performance of directly applying anomaly detection
techniques is poor, as illustrated in both Ex ample 1 below
and experiments in Section 6.
On the other hand, constraint-based repairing SCREEN
[22], strictly following the minimum change principle in data
repairing [1], heavily relies on a proper constraint of speeds
on value changes. The repairing is p erformed based on two
consecutive points, i.e., considering only one historical point,
and thus does not sense the temporal nature of errors. As
shown in the following Example 1, the speed constraint-
based SCREEN is effective in repairing spike errors, but
can hardly handle a sequence of consecutive dirty points.
1046
22
22.5
23
23.5
24
24.5
25
25.5
26
26.5
27
27.5
360 365 370 375 380 385 390 395 400
Value
Time
Observation
Truth IMR
EWMA
SCREEN
ARX
Truth
IMR
SCREEN
ARX
EWMA
Observation
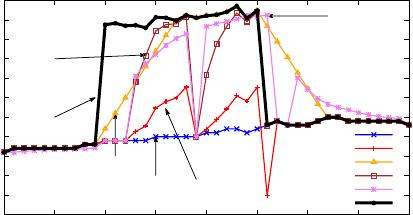
Figure 1: An example segment of sensor readings
In short, the anomaly detection method does n ot expect
the minimized mistakes in practice, whereas the constraint-
based repairing is not effective in addressing the temporal
nature of errors.
1.3 Intuition of Our Proposal
Since completely automatic data repairing might not work
well in repairing t ime series data (such as SCREEN [22] ob-
served in our ex periments in Figure 9), enlightened by the
idea of utilizing master data (a single repository of high-
quality data) in data repairing [9], we employ some labeled
truth of dirty observations to advance the repair. The truth
can be obtained either by manual labeling or automatically
by more reliable sources. For instance, accurate locations
are manually marked in the map by user check-in activ-
ities (and utilized to repair th e imprecise GPS readings).
Moreover, periodical automatic labeling may take place in
certain scenarios, e.g., precise equipments report accurate
air quality data (as labeled values) in a relatively long sens-
ing period, while crowd and participatory sensing generates
unreliable observations in a constant manner [28].
Being aware of both the error nature in anomaly detec-
tion and the minimum change principle in data repairing,
we propose iterative minimum repairing (IMR). The phi-
losophy beh ind the proposed iterative minimum repairing
is that the h igh confi dence repairs in the former iterations
could help the latter repairing. Specifically, IMR minimally
changes one point a time to obtain the most confident repair
only, referring to t he minimum change principle in data re-
pairing that human or systems always try to minimize their
mistakes. The high confidence repairs, together with the
labeled truth of error points, are utilized to learn an d en-
hance the temporal nature of errors in anomaly detection,
and thus generate more accurate repair candidates in the
latter iterations.
Example 1. Figure 1 presents an example segment of sen-
sor readings, denoted by black line. Suppose that sensor er-
rors occur in the period from time point 370 to 385, where
the observations are shifted from the truth, e.g., owing to
granularity mismatch or unit error. To repair the errors,
the truth of several observations are labeled, including time
points {370, 371, 372, 379, 387}.
Existing speed constraint-based cleaning (SCREEN) [22]
could not effectively repair such continuous errors in a pe-
riod (which is indeed also observed in Example 1 in [22]).
The reason is that speed constraints, restricting the amount
of value changing relative to time difference, can detect sharp
deviations such as from time point 369 to 370, but not con-
tinuous errors, e.g., in 383 and 384. The exponentially
weighted moving average (EWMA) [13] algorithm also hard
to find a proper way to clean the trace. These two methods
have similar repair trace.
By considering the predication values in anomaly detection
as repairs (see m ore details in Section 2), the result of AR X
based repairing is also reported. ARX, considering the errors
between truth and observations, shows better repair results
than EWMA and SCREEN methods.
Finally, our proposed IMR approach, with both error pred-
ication and minimum change considerations, obtains repairs
closest to the truth.
The iterative minimum repairing leads to new challenges:
(1) whether the repairing process converges; and (2) how to
efficiently/incrementally update the parameter of the tem-
poral model over the repaired d ata after each iteration. Both
issues in anomaly repairing are not considered in the anomaly
detection studies.
Contributions. Our major contributions in this paper are
summarized as follows.
(1) We formalize the anomaly repairing problem, given a
time series with some points having labeled truth, in Section
2. The adaption of existing anomaly detection techniques
(such as AR and ARX) is introduced for anomaly repairing.
(2) We devise an iterative minimum-change-aware repair-
ing algorithm IMR, in Section 3. Remarkably, we illustrate
that the ARX-based approach (in Section 2) is indeed a spe-
cial case of IMR with static parameter (Prop osition 2).
(3) We study the convergence of IMR in various scenarios,
in Section 4. In particular, the convergence is explicitly ana-
lyzed for the special case of I MR(1) with order p = 1, which
is sufficient to achieve high repair accuracy in p ractice (as
shown in the experiments in Section 6). We prove that under
certain inputs, the converged repair result could be directly
calculated without iterative computing (Proposition 8).
(4) We design efficient pruning and incremental computa-
tion for parameter estimation in each repair iteration, in Sec-
tion 5. Rather than performing parameter estimation over
all the n points, matrices for parameter estimation could be
pruned by simply removing rows with value 0 (Proposition
9). It is also remarkable that the incremental computation
among different repair iterations (Proposition 10) could fur-
ther reduce the complexity of parameter estimation from
O(n) to O(1).
(5) Experiments on real datasets with both real and syn-
thetic errors, in Section 6, demonstrate that ou r IMR method
shows significantly better repair performance than the state-
of-the-art approaches, includ ing the aforesaid anomaly de-
tection and constraint-based repairing.
Table 1 lists the notations frequently used in this pa-
per. All the proofs can be found in the full technical report
(http://ise.thss.tsinghua.edu.cn/sxsong/doc/anomaly.pdf).
2. PRELIMINARIES
This section first introduces the problem of anomaly re-
pairing. We then adapt the existing anomaly detection mod-
els for anomaly repairing, i.e., AR without considering la-
beled data and ARX supporting labeled data.
1047
of 12
免费下载
【版权声明】本文为墨天轮用户原创内容,转载时必须标注文档的来源(墨天轮),文档链接,文档作者等基本信息,否则作者和墨天轮有权追究责任。如果您发现墨天轮中有涉嫌抄袭或者侵权的内容,欢迎发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。
下载排行榜


文档被以下合辑收录
评论